| Revision as of 13:04, 31 January 2015 editTomruen (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers119,883 edits →gallery in the article← Previous edit | Revision as of 13:07, 31 January 2015 edit undoTomruen (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers119,883 edits →gallery in the articleNext edit → | ||
| Line 840: | Line 840: | ||
| :::::::I've cut it down to eight pictures: 2{3}, 3{3}, 2{4}, 2{5}, 2{5/2}, 3{5/2}, 2{7/2}, and 2{7/3}. I think that ought to be enough for the reader to get the point. (Once the digon pictures are available, I'd consider putting 2{2} and 3{2} in as well, perhaps kicking out the heptagrams.) ] (]) 11:44, 31 January 2015 (UTC) | :::::::I've cut it down to eight pictures: 2{3}, 3{3}, 2{4}, 2{5}, 2{5/2}, 3{5/2}, 2{7/2}, and 2{7/3}. I think that ought to be enough for the reader to get the point. (Once the digon pictures are available, I'd consider putting 2{2} and 3{2} in as well, perhaps kicking out the heptagrams.) ] (]) 11:44, 31 January 2015 (UTC) | ||
| ::::::::Thank you. I regard the reduction from 30 + 2 to 8 as a great improvement. I'd suggest that only one star compound of digons would be enough, say 3{2}. — Cheers, ] (]) 11:53, 31 January 2015 (UTC) | ::::::::Thank you. I regard the reduction from 30 + 2 to 8 as a great improvement. I'd suggest that only one star compound of digons would be enough, say 3{2}. — Cheers, ] (]) 11:53, 31 January 2015 (UTC) | ||
| ::::::::: I added a row of digon compounds. Trim away as your heart desires, but one example is a sad sad world. ] (]) 13:07, 31 January 2015 (UTC) | |||
Revision as of 13:07, 31 January 2015
| Mathematics C‑class Mid‑priority | ||||||||||
| ||||||||||
Gallery
Regular star polygon graphs
I generated SVG images for all regular star polygons up to 32 sides, specifically {p/q}, q<p/2 and gcd(p,q)=1. It's a bit long for the article, so I put them here for reference. I copied ons up to 20 at List_of_regular_polytopes#Stars. Tom Ruen (talk) 09:35, 22 January 2015 (UTC)
Regular star figures graphs
Here's some star figures (compounds) too, n{p/q} with p=2..16, q=1..p/2, and n*p<32. I colored the edges, but looks like yellow was a poor color choice. Tom Ruen (talk) 10:52, 22 January 2015 (UTC)
Isogonal stars
These star polygons are isogonal (vertex-transitive), all solutions for equal-spaced vertices, p=3..16. They have two edge lengths in general, while some have equal edge lengths and are also regular: t{p/q}={2p/q} for odd(q), and t{p/(2p-q)}={2p/(2p-q)} for odd(2p-q). Tom Ruen (talk) 04:01, 29 January 2015 (UTC)
definition of "star" polygons
The introduction says that "star" polygons are by definition regular, which surprises me. Is there really such a convention? What would you call the figure formed by the diagonals of an irregular (but convex) pentagon? —Tamfang 06:36, 23 March 2006 (UTC)
- I was surprised also. It implies "star"="regular nonconvex", so anything else is merely "nonconvex" or "complex". I don't have an explanation for the definition limitation. Tom Ruen 09:36, 23 March 2006 (UTC)
- I was also surprised, but I checked another reference and it also does say they are regular. of course, since most of the interesting properties are numeric rather than geometric, it doesn't actually matter. -- Securiger 08:52, 28 August 2006 (UTC)
I removed this, doesn't belong in generalized article on geometry - please move to pentagram if anyone wants to keep it! Tom Ruen 03:28, 27 September 2006 (UTC)
- It has been stated that creating a five-pointed star in a similar fashion was one of the esoteric teachings of the Pythagoreans. Divulging that secret was punishable by death.
This article is a bit of a mess. I rearranged a bit, but needs more work.
Also there's also two distinct definitions of star polygon used in Branko Grunbaum's book Tilings and Patterns (Chapter 2, section 5), the other meaning from Kepler, which actually considers concave simple 2n-gons as the outlines of a complex connected n-gon (shown here), and used in tilings. Grunbaum uses notation |m/n| for these concave form. He also uses {nα}, for an n-sided star with vertex internal angle α<180*(1-2/n). Anyway, thought I'd throw this out here in talk at least, while not prepared to add anything for now. Tom Ruen 03:38, 27 September 2006 (UTC)
- Is a star actually able to be considered a geometric shape? Stars vary in the amount of vertices and sides. All geometric shapes, when defined as whatever shape, is mentioned to have this many sides and this many points. To have less points or less sides classifies it as a different shape (if physically possible). Ulgar 19:21, 30 July 2007 (UTC)
- Sorry, I don't understand your question. Tom Ruen 19:32, 30 July 2007 (UTC)
- The term "star" defines a class of geometric shapes, in the same way that a term like "polygon" or "configuration" does. Some classes of shape are defined according to some number, such as the class of pentagons, but other classes are not. And some classes overlap, such as stars and pentagons. An individual shape may then be described specifically, such as a "regular star pentagon" or "Reye's configuration." Hope this helps. -- Steelpillow 20:13, 30 July 2007 (UTC)
- Ah, thank you, Steelpillow. In all honesty, a friend and I were arguing about whether stars could be considered a shape like square and pentagon and rhombus. The definition of a star was one of where a person goes from the point of one to another blah blah blah... it wasn't as the other shapes. However, putting it into that shapes are actually just different categories of which all polygons can fall under, I see now how the category "star" can exist, because its defining sets of rules differ from other typical categories like square and pentagon and rhombus. Now that I think of it, I should have paid more attention to that different shapes can have the same number of sides and vertices but MORE qualifiers like angle. I guess I lose the argument. :P Ulgar 01:45, 1 August 2007 (UTC)
Definition revisited
Two contributors have recently made changes to the lead definition. Also, Tamfang has edited the discussion of regular compounds. I do not agree fully with these changes, so I have reverted them in the hope that we can reach agreement here before making further changes.
An anonymous visitor talked about the "artistic depiction of a star". I do not think I am the only one dissatisfied with this - there is no aesthetic or cultural judgement, and hence no "art" in the mathematical concept: it is a pragmatic description.
- That'd be me (my username is Popisfizzy). I changed it because when I think "star", I tend to think moreso of the spherical cellestial objects makes of plasma, and not the geometric shape. I suppose I shouldn't've been so hasty. 207.255.35.246 (talk) 05:39, 21 January 2009 (UTC)
Tamfang talks about the diagonals of a convex polygon (a process called facetting). While this is true, a star polygon may also be constructed by extending the sides of, or stellating, a convex polygon. These processes are dual to each other, and are both equally significant. Neither process defines what a star polygon is.
I agree that the current lead is not satisfactory either, but I think it has the basics about right. I would suggest something along the lines of:
- "A star polygon is a non-convex polygon which looks in some way like a star. Only the regular ones have been formally defined and studied in any depth; star polygons in general have never been formally defined. They are not the same thing as polygons which are star domains."
I also retrieved the difficulty over compound stars and Schläfli symbols. This is a deep one - its origin goes back to Poinsot, and the modern usage has only recently become established (or maybe it hasn't yet and we need to discuss both usages?).
-- Cheers, Steelpillow (Talk) 11:39, 18 January 2009 (UTC)
- Well, you know, any stellated polygon consists of diagonals of its convex hull. Any convex polygon (>4) has diagonals that can make a star, but not every such polygon can be stellated, because of parallel edges. —Tamfang (talk) 17:50, 18 January 2009 (UTC)
Now I come to think about it, self-intersecting polygons exist which cannot be constructed in this way. In general for such a polygon, one or more vertices may lie within the body of the convex hull. It has not to my knowledge been decided whether such a polygon may be included among the stars or should be excluded. (Of course regular stars behave sensibly, but here we are considering stars in general). As for the remark about parallel edges, even this is not true in the projective plane or on the sphere. -- Cheers, Steelpillow (Talk) 21:28, 18 January 2009 (UTC)
- Good point about the convex hull. On the other hand, if I say definition X is not general enough to cover condition Y it's no refutation to point out that it does cover condition Z – unless you're proposing to confine the discussion to the projective plane! —Tamfang (talk) 03:39, 19 January 2009 (UTC)
No. OTOH I do not propose to confine it to the Euclidean plane either. -- Cheers, Steelpillow (Talk) 12:03, 19 January 2009 (UTC)
Article now updated. -- Cheers, Steelpillow (Talk) 12:42, 21 January 2009 (UTC)
On a private mailing-list someone suggested locally but not globally convex, which covers all the figures in the article but not (for example) bowties or darts. —Tamfang (talk) 18:16, 31 January 2009 (UTC)
- The idea of local convexity does in fact include bow-ties, because each vertex (the "local" one) is considered in isolation. But sadly all that is unpublished OR and we cannot include it. -- Cheers, Steelpillow (Talk) 20:08, 31 January 2009 (UTC)
Merge with star polyhedron?
I don't support a merge - it's like saying merge polygon and polyhedron. The other article is short and needs expanding, but this one also can use expanding as well - including Kepler's definition of stars for tilings. Tom Ruen 17:42, 3 August 2007 (UTC)
- It is also worth comparing with stellation, which IS a multidimensional article now. Stellations and polytopes are closely related in appearance, but also categorically different constructions and topology. Tom Ruen 17:45, 3 August 2007 (UTC)
- Merging is quite wrong. I'm removing the suggestion -- Steelpillow 07:47, 4 August 2007 (UTC)
comments on lead
I came across this article after linking from Circle of fifths and it has some very nice graphics. It would be interesting to know more about the history. Why did Thomas Bradwardine study these and what did he conclude? Comments above mention Kepler, but he is not named in the article. More about his contributions would be interesting too.
Is there a way to rephrase the lead so that it doesn't sound so much like a confession of ignorance and helplessness? To be honest, my first thought when I read the lead was that it had been vandalised by a prankster, but that is not so. The lead merely needs to summarize what is already in the article, and the article describes both regular and irregular star polygons.
Here is a suggested copyedit of the lead:
- In geometry, a star polygon is a polygon that has a starlike shape.
- Examples of regular star polygons are the pentagram and the hexagram.
- Regular star polygons were first studied systematically in the 14th century by Thomas Bradwardine and were also studied by Kepler.
If there are several alternative definitions of any terms, the lead could say so, although the article would need to give the details.
In the definition of a regular star polygon, the phrase "created by" implies a creator.
--Jtir (talk) 13:36, 29 July 2008 (UTC)
- There is a difficulty with definitions in that one might expect from the grammatical construction of "regular star polygon" that it would indicate a regular example of the more general star polygon. In fact it arose as a starlike example of the more general regular polygon. This leads to the further difficulty that the idea of a "star" figure has never (to my knowledge) been defined outside of the context of regular figures (although star-like polygons have been defined - to mean something else). To define it as suggested is to break new ground and is not acceptable.
- Then, references to Bradwardine and Kepler come pretty much from Coxeter's Regular Polytopes, which says very little more about them. We would have to kidnap a historical scholar if we wanted to find out more. Meanwhile, I think that a History section would be nice. It could start with ancient pentagrams and a few others (IIRC heptagrams and enneagrams from Mediterranean civilisations, but don't quote me on that). Thence, via Bredwardine and Kepler, to Poinsot's approach. Wish I had the time to research it properly.
- As for irregular ones, I personally think the whole section should go, as it has no foundations worth the name and is basically just speculation (unless someone knows better?).
- Anyway, the whole thing is still pretty embryonic, IMHO. If you can figure a way to improve it, please go ahead - it is not in a finished enough state for anybody to get upset.
- HTH -- Cheers, Steelpillow (Talk) 19:28, 29 July 2008 (UTC)
- Thanks for your reply. From your comments and a google search, I believe that the section on "Irregular star polygons" is original research and could be removed on that basis. I have tagged it with {{Original research}}. (I know very little about this subject, so if someone cites a reliable source defining the term, that is fine with me.)
- "...grammatical construction...": OK. It sounds like the the term "regular star polygon" is used, but there is no general theory of "star polygons", so the terms "regular star polygon" and "star polygon" are essentially synonymous. Is that correct?
- There seems to be plenty of material justify a History section.
- --Jtir (talk) 21:13, 29 July 2008 (UTC)
- Thanks Tom. I tried harder and found two more sources using the term "irregular star polygon":
- What does this mean for what the lead says?
- --Jtir (talk) 21:53, 29 July 2008 (UTC)
- I referenced in the USE of irregular star polygons as the vertex figures for the uniform polyhedra, but I accept Coxeter never names them as anything but polygonal vertex figures. Gruenbaum says "star polygons" are regular, so its a matter of definitions. You could call Coxeter's vertex figures as nonconvex cyclic polygons, or whatever if the "star" name is reserved for regularity. The there's also other graphs like Unicursal hexagram that are not regular but definitely a nonconvex polygon again. So that's about all I know, without doing more reading from my varied sources. Tom Ruen (talk) 22:24, 29 July 2008 (UTC)
- Thanks for the additional info. Since this is an encyclopedia, editors don't have to choose one definition, but rather describe the various terms and their definitions:
- star polygon (Gruenbaum)
- star polygon (numerous sources at google books)
- regular star polygon (numerous sources)
- polygonal vertex figure (Coxeter)
- irregular star polygon (Gardener) (Is this source relevant to this article?)
- In an earlier comment you said Gruenbaum gives two defs, one of which is from Kepler (IIUC). Does he distinguish the two meanings with special terminology?
- You guys know far more about this than I do, but ISTM that the overreaching term here might be "Nonconvex polygon" and that this might be a better name for the article, since the scope of the article seems to be broader than Gruenbaum's "star polygon". ATM, Nonconvex polygon is a redirect to Complex polygon. Does that seem reasonable?
- Thanks for the additional info. Since this is an encyclopedia, editors don't have to choose one definition, but rather describe the various terms and their definitions:
- Presenting irregular star polygon as though it is an accepted technical term is, IMO, very close to original research. A possible solution is to call the section polygonal vertex figures for the uniform polyhedra, say, and then note that these could be considered irregular star polygons (that would be more like paraphrasing than OR).
- --Jtir (talk) 23:38, 29 July 2008 (UTC)
- Yes, Gruenbaum's Tilings and Patterns does has TWO definitions, Keplers (concave 2n-gonal polygons with an "alpha" angle parameter, not explained here) for tiling, and the nonconvex forms given in this article. He does have a different notation like {5/2} for a pentagram and |5/2| for the concave decagon with the same exterior, and a third {5α} for the parametric variations. I basically never got around to documenting Kepler's forms because I was more interested in the uniform polyhedrons which used the intersecting forms.
- On merging/moving to nonconvex polygon, with all the varied uses. I'm just too lazy to really expand it all. I guess until something is written about Kepler's tilings, there's little point in describing the tiles. Tom Ruen (talk) 23:50, 29 July 2008 (UTC)
- Thanks, that's very interesting. It sounds like a section on Kepler's forms would make sense. It could be started as a stub section and tagged as needing expansion with {{Expand-section}}.
- If Gruenbaum doesn't distinguish the two definitions by name, editors will need to. Any ideas on how to do that?
- Here is a definition of "irregular" from Coxeter:
- "A completely irregular figure has no symmetry save identity." The Beauty of Geometry: Twelve Essays By H. S. M. Coxeter (Dover, 1999)
- The vertex figure in the article appears to have some symmetry.
- Here is a definition of "irregular" from Coxeter:
- It occurs to me that if a "star polygon" is regular by definition, then "regular star polygon" is redundant, yet the term seems to be commonly used. I now see what Steelpillow meant: "regular polygon that is star-shaped" -> "star-shaped regular polygon" -> "star regular polygon" -> "regular star polygon". Notwithstanding my amateur etymology, this suggests that the article ought to say something about this possibly misleading grammatical construction. The term distinguishes a subclass of regular polygons, not a subclass of star polygons. Whew! :-)
- Would it be fair to say that "star polygon" is simply an abbreviation of "regular star polygon"?
- If so, the lead could say something like: "... a regular star polygon (often abbreviated to star polygon) ..."
- --Jtir (talk) 15:24, 30 July 2008 (UTC)
Some further thoughts. Grunbaum famously remarked that "the original sin" in the theory of regular polyhedra was a failure to define the polyhedra of which one sought the regular variety. Remarks in his book Convex polytopes are often taken out of context because he did not repeat the word "convex" a few thousand times and mostly just referred to "polytopes". Similarly, remarks about regular figures often drop the tedious "regular". So read Tilings and patterns carefully with these thoughts in mind.
Did Gardner define the "star polygons" of which he sought the irregular variety? Did Strader & Rhodes? By contrast, Mathworld is typical of popular folklorists in unquestioningly assuming regularity.
"Nonconvex" refers to many kinds of shape; most of them are not what one would think of as stars - an arrowhead-shaped quadrilateral for example. "Star-like" is defined broadly thus: can a point within the polygon be found, such that any ray drawn from that point meets the perimeter exactly once? If so, then the polygon is star-like. It follows that all convex polygons are star-like. And a decagon that "looks like" a star pentagon is a star-like polygon (and not a star polygon).
Expect nothing but confused folklore from the internet (e.g. Mathworld) or from most other places. Authoritative treatments are hard to find. Does Tilings and patterns discuss star polygons independent of their regularity? If all else fails, I could email Branko and ask him.
-- Cheers, Steelpillow (Talk) 21:38, 30 July 2008 (UTC)
- Thanks for your thoughts and your paraphrase of Grunbaum. That confirmed my suspicions that "star polygon" may sometimes be an abbreviation of "regular star polygon" and that the lead needs to note this fact and the fact that some sources (e.g. Mathworld) define the term "star polygon" to mean that it is regular.
- Unless someone cites a reliable source otherwise, I am assuming now that there is no such thing as a general theory of star polygons.
- I cited Gardner, S&R, and Coxeter as among the few credible examples of the use of "irregular" at google books (I did not do a lit search, because you guys are the experts). What is your opinion of Coxeter's def? Would it be widely accepted? BTW, you can read the text of Coxeter and Gardner yourself at the links I provided. (It took me some actual work to assemble them, so I hope editors will take advantage.)
- I apologize if you already know this: The name of an article does not need to exactly match the boldface name in the lead.
- Star-shaped polygon has a note that the term is distinct from "star polygon". This article needs to say the same.
- What is your opinion of this def from Regular polygon?
- "A non-convex regular polygon is a regular star polygon."
- --Jtir (talk) 00:18, 31 July 2008 (UTC)
- This edit has a summary that reads:
- "Star polygons do not have to be regular - see Cromwell ref, p.250."
- Here is page 250 of Cromwell.
- This page provides an excellent example of regular star polygon being abbreviated to star polygon.
- Where does he state or imply that "Star polygons do not have to be regular"?
- He seems to implicitly define "irregular" here:
- "What distinguishes a symmetrical object from an irregular one?" (Cromwell, p. 290)
- How would editors interpret this?
- --Jtir (talk) 14:51, 31 July 2008 (UTC)
- This edit has a summary that reads:
- I'm afraid as User:Steelpillow suggests definitions (from the horribly disappointing opening of this article), they are rot all the way down, never globally defined/limited, just starting with the simplest and extended as people find uses for them. That said, it doesn't mean improvement can't be made.
- Well, one idea worth looking for support, it does seem like cyclic polygon is one requirement that groups regular and irregular polygons of interest. (Irregular meaning simply not regular.)
- Another related article Star polyhedron, although exclusively about regular and uniform forms. (Uniformity isn't a separate category for polygons because defined to be same as regularity.)
- Tom Ruen (talk) 20:13, 31 July 2008 (UTC)
- Thanks. It sounds like you are suggesting an article on cyclic polygons (which is now just a redirect to Circumscribed circle) and that such an article would have enough scope to cover both regular star polygons and Coxeter's vertex figures. That sounds reasonable to me, although I can't really comment on the technical merits. However, regular star polygons is clearly a big enough topic to need its own article, so an article on cyclic polygons could use summary style to summarize RSPs and link to this article as the main article. --Jtir (talk) 18:41, 1 August 2008 (UTC)
Collected responses
First, a correction. Above I said that a concave decagon having the outline of a pentagram is not a "star polygon". Re-reading other comments, it appears that according to Kepler's definition it is.
User:Jtir says "Unless someone cites a reliable source otherwise, I am assuming now that there is no such thing as a general theory of star polygons." That is my understanding, exactly.
And again, "I cited Gardner, S&R, and Coxeter as among the few credible examples of the use of "irregular" at google books (I did not do a lit search, because you guys are the experts). What is your opinion of Coxeter's def? Would it be widely accepted?" Coxeter defines "completely irregular" rather than just plain "irregular". What about quasiregular, semiregular or mirror-symmetric figures - these are not "regular" but neither are they "completely irregular". He is using "completely irregular" as a synonym for "asymmetric".
Again, "What is your opinion of this def from Regular polygon? ... "A non-convex regular polygon is a regular star polygon." That is true, but badly written (I think I wrote it, ooer.) since it implies they are two different names for the same thing. It is better to say something like, "For a non-convex polygon to be regular, it must be a regular star polygons."
Like Mathworld, Cromwell is a bit of a folklorist. He draws what is presumably meant to be an irregular star pentagon, makes some throwaway remark which does not reference the figure depicted, and rushes on to the regular variety. useless. Actually, Mathworld is even worse: Coxeter's Regular polytopes talks about star polygons - like Grunbaum, Coxeter does not bother to repeat "regular" several thousand times, the clue is in the book title, but this does not stop Mathworld from assuming regularity in its standalone web page.
And yet the idea of "irregular star polygons" does crop up now and then, and cannot be dismissed. I think the best approach is to say that of the star polygons, only the regular ones have an accepted definition.
-- Cheers, Steelpillow (Talk) 08:10, 1 August 2008 (UTC)
- Thanks. The basic problem with using "irregular" in the article is that it is not defined in the article, and, as editors have noted, there is more than one possible definition. Further, editors cannot simply stipulate a definition, because that would be original research. I agree that the article needs to mention the term "irregular star polygon" and note that the term is used occasionally. I did a lit search and found one example of it being used, so we have all of three examples:
- Flaten, James A. 1999. "Curves of Constant Width." Physics Teacher 37, no. 7: 418. MasterFILE Premier, EBSCOhost (accessed August 1, 2008).
- A search for "regular star polygon" turned up only one match, so my library may not have the right databases for researching the usage of these terms. Could one of you guys do a lit search?
- While Mathword has its faults, I regard it as a valuable resource. MW's use of the unqualified term "star polygon" may be non-standard, but that is simply a fact that editors can note in the article.
- --Jtir (talk) 19:51, 1 August 2008 (UTC)
- We come back again to the problem that many respected authors, even standard authorities, have used phrases like "star polygon", and maybe mentioned irregular ones, without ever defining what they were talking about - and often one finds subtly different assumptions, unstated, between different authors (e.g. are they by definition regular?). Professional mathematicians, or any others for that matter, have simply not cared about the idea enough to create a knowledge base capable of sensible (i.e. encyclopedic) discussion. Only when we get to high symmetry - regular and uniform stars - do we find a suitable body of work out there. All of which underlies my original instinct to just delete the section on irregular star polygons.
- Your library's lack of references for "regular star polygon" is probably because the salient discussions appear under "star polygon", with regularity blandly assumed by the author. It is only when other authors discuss less regular types, such as uniform star figures, that we discover the assumption of regularity to be unjustified. It suddenly occurs to me that the best thing might be to repurpose the "irregular" section as "Uniform" or "Semiregular" star polygons.
- -- Cheers, Steelpillow (Talk) 08:49, 2 August 2008 (UTC)
- I would favor removing the section called "irregular star polygons" and moving the info about Coxeter's vertex figures to another article. IIUC, one possibility would be to move it to a new article on cyclic polygons. Another would be to start a new article exclusively about Coxeter's vertex figures (not sure what its name would be, though). Any other suggestions?
- ISTM, that the scope of this article is "regular star polygons", which a large enough topic already.
- Thanks for suggesting the broader search — a search for "star polygon*" (singular and plural at ArticleFirst) found 10 items, many of which appear to be relevant to this article. Interestingly, some appear to be written for teachers.
- --Jtir (talk) 10:51, 2 August 2008 (UTC)
- Coxeter's vertex figures appear in the context of the uniform polyhedra and should be discussed there. The cyclic issue is mostly a red herring: the general cyclic polygon is wholly irregular. However, it is relevant to (all) regular and uniform/semiregular polygons, so these sections could have links to it.
- Note that "star-shaped" means the same as "star-like", i.e. some point can be found from which all rays intersect the boundary only once, so all convex polygons are star-shaped but not stars, while a pentagram is a star but is not star-shaped. Don'cha just luurve the instinctive logic and rigor of the mathematical mind ;-p ?
- Which still leaves your library with surprisingly few hits on "star polygon", regular or otherwise. There must be many papers, some seminal, by Coxeter, Grünbaum (alone or in collaboration with Shepherd) and probably others, not to mention Poinsot's 'Memoire sur les polygones et polyedres. Certainly, standard reference works by Coxeter, Cromwell and Wenninger use the phrase.
- -- Cheers, Steelpillow (Talk) 13:13, 2 August 2008 (UTC)
- The ArticleFirst cut-off date is 1990, and there is nothing specific given for MasterFILE Premier. Someone with access to an academic library might do better.
- Jordan normal form documents another case of redundant and ambiguous terminology.
- --Jtir (talk) 23:58, 2 August 2008 (UTC)
History
Placing a subheading here to highlight the value of a History section, as mentioned a couple of times in the above. -- Cheers, Steelpillow (Talk) 08:10, 1 August 2008 (UTC)
- Promoted to a section, so it can be used to collect sources. --Jtir (talk) 18:21, 1 August 2008 (UTC)
- This seems to have Kepler's study of regular polygons in a recent scholarly edition:
- The Harmony of the World By Johannes Kepler, E. J. Aiton, Alistair Matheson Duncan, Judith Veronica Field (1997) (worldcat)
- A brief outline of the history:
- College Geometry By Howard Whitley Eves (1995)
Literature search results from the ArticleFirst datebase
The search was for "star polygon*" (with wildcard after "polygon"), and the results are sorted by date.
--Jtir (talk) 11:03, 2 August 2008 (UTC)
Title: Covering Orthogonal Polygons with Star Polygons: The Perfect Graph Approach. Source: Journal of computer and system sciences. 40, no. 1, (February 1990): 19 Title: On Covering Orthogonal Polygons with Star-Shaped Polygons. Source: Information sciences. 65, no. 1 and 2, (1992): 45-64 Title: Recognizing S-star polygons Source: Pattern recognition. 28, no. 7, (1995): 1019 Title: A classroom note on the regular polygon and an associated star. Source: Mathematics and computer education. 30, no. 1, (Winter 1996): 6 Title: The Determination of the Elastic Field of a Polygonal Star Shaped Inclusion Source: Mechanics research communications. 24, no. 5, (1997): 473 (10 pages) Title: Position-Independent Near Optimal Searching and On-Line Recognition in Star Polygons Source: Lecture notes in computer science. no. 1272, (1998): 284 Title: Angle Sums of Star Polygons Source: Mathematics in school. 32, no. 4, (2003): 26 (2 pages) Title: Searching and on-line recognition of star-shaped polygons Source: Information and computation. 185, no. 1, (2003): 66 (23 pages) Title: Note on covering monotone orthogonal polygons with star-shaped polygons Source: Information processing letters. 104, no. 6, (2007): 220 (8 pages) Title: Mathematical Lens - Star Polygons Source: The Mathematics teacher. 101, no. 6, (2008): 432 (8 pages)
irregular star polygon example
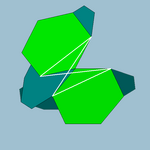
 2-isogonal star 9/4 |
 Regular star {9/4} |
If we want an example irregular star polygon (with a high symmetry), one exists in the echidnahedron article as its polyhedral face. THe picture above compare the regular form. They have the same winding 9/4, but the first has vertices that are not evenly spaced on a circle. Tom Ruen (talk) 22:45, 3 August 2008 (UTC)
Quadrilateral (bow-tie) examples
Uniform polyhedron vertex figures: (White lines)
- Many more at List of uniform polyhedra
- Tom Ruen (talk) 00:02, 4 August 2008 (UTC)
Irregular remarks in the lead, again
User:Taxman recently changed the lead, and commented that many definitions of a general star polygon may be found. I have seen many definitions of a regular star polygon. Often these will assume regularity and not make it explicit; Mathworld is a typical example of this sloppiness. If there are genuine definitions out there, applicable to irregular star polygons, please feel free to give the definition in the article (and of course add the reference). If in doubt, it might be better to post the definition here so we can run over it (for example any definition which discusses Schläfli symbols is likely to apply only to the regular variety, whether or not the author realised this at the time). -- Cheers, Steelpillow (Talk) 19:40, 8 July 2009 (UTC)
- If your beef is with definitions not covering irregularity, then your lead sentence should state that more explicitly. As it is the sentence doesn't sound very good. Also to be pedantic you'd need a reference for such a strong statement as have never been..., which isn't likely to exist, so it's better to reword to something that can be supported by the available references, not original research. - Taxman 01:03, 9 July 2009 (UTC)
- I don't like beefing about others' work too much in articles - save that for the discussions. Also to be pedantic, a statement implying that no references exist can hardly be backed up by a reference. OTOH you only need a single one to refute my statement (you originally claimed there are many). Meanwhile, if you can find a better form of words to express what is currently intended, then I have no problem with that. Your remarks have spurred me to have a quick go myself, but there is probably still room for improvement. -- Cheers, Steelpillow (Talk) 19:32, 9 July 2009 (UTC)
Merger proposal
It seems a little silly to have two articles about the same subject. Clarityfiend (talk) 00:07, 19 September 2012 (UTC)
- No - Keep them separte. Mathematically, the idea of a polygon is quite a general idea. Thare are some important sub-types, including for example convex, regular, star and abstract. I'd suggest that each of these important sub-types needs separate treatment in a specialist article (for example abstract polygons are covered in the article on abstract polytopes.— Cheers, Steelpillow (Talk) 18:43, 21 September 2012 (UTC)
- The articles are about the same subject, but one is from the mathematical perspective, and one from the symbolic. It's obvious to me that these areas need to be treated separately, but in the same article. --St. Nerol (talk) 22:38, 13 January 2013 (UTC)
gallery in the article
I removed the gallery of star polygons because it adds nothing encyclopedic to the encyclopedia. For more, see WP:GALLERY AND WP:NOTGALLERY. — Cheers, Steelpillow (Talk) 09:15, 31 January 2015 (UTC)
- Some people like you like to read words to understand a concept. Some people like me prefer pictures first. Small examples ADD value even if you don't need it personally. Tom Ruen (talk) 09:25, 31 January 2015 (UTC)
- By no stretch of the imagination is that a "small" gallery. And now you are warring in defiance of BRD - that is really not good. I suppose I could throw quotes from those policy & guideline pages at you and you could argue around the form of words claiming justification, but I'd rather take it straight to the Maths wikiproject. — Cheers, Steelpillow (Talk) 09:31, 31 January 2015 (UTC)
- I don't understand you. A gallery is a random collection of related images with NO TEXT. There is no gallery! Tom Ruen (talk) 10:09, 31 January 2015 (UTC)
- p.s. I didn't know what BRD was, but seems to be this Misplaced Pages:BOLD, revert, discuss cycle. I've not done a single simple revert, and have attempted compromised improvement every edit. Tom Ruen (talk) 10:14, 31 January 2015 (UTC)
- OK, so. First, you don't need a gallery tag to make something a gallery. Any big block of images is a gallery to the reader, even if the editor concerned carefully avoids the <gallery> code. Second, that an editor of your long experience has never come across a WP:BRD link beggars belief. Still, if you say so. Third, here is the chain of your bold edit - my deletion - your direct counter-revert - my repeat edit invoking BRD - your second revert. Both those reverts of your were direct reverts of my deletions which flagged up notifications to me as such, so how you can claim that you have not done any also beggars belief. Further, after reading WP:BRD you have continued to pile on the images instead of conforming. Sorry Tom, but I find your pleas to be specious and your conduct to be unacceptable. — Cheers, Steelpillow (Talk) 10:44, 31 January 2015 (UTC)
- Nope, I never heard of WP:BRD at least as an acronym, and again, EVERY revert of your revert, I tried a compromise edit, first using less examples, and then looked to integrate it better with the text. So its your privledge to be offended, but I've done all the work here. I only feel bad for not having any degenerate example images described in the text... {4/2}=2{2}, {6/3}=3{2}, etc. Tom Ruen (talk) 10:52, 31 January 2015 (UTC)
- You could (and IMHO should) certainly add a few of the degenerate ones. Do they give any problems with whatever you're using to generate them? If not, Tyler ought to work (and you can then colour the individual digons in the compound). Double sharp (talk) 11:05, 31 January 2015 (UTC)
- No problem, I just didn't generate them in my first set of images, but they are the most starry! Tom Ruen (talk) 11:27, 31 January 2015 (UTC)
- You could (and IMHO should) certainly add a few of the degenerate ones. Do they give any problems with whatever you're using to generate them? If not, Tyler ought to work (and you can then colour the individual digons in the compound). Double sharp (talk) 11:05, 31 January 2015 (UTC)
- Nope, I never heard of WP:BRD at least as an acronym, and again, EVERY revert of your revert, I tried a compromise edit, first using less examples, and then looked to integrate it better with the text. So its your privledge to be offended, but I've done all the work here. I only feel bad for not having any degenerate example images described in the text... {4/2}=2{2}, {6/3}=3{2}, etc. Tom Ruen (talk) 10:52, 31 January 2015 (UTC)
- Did you perhaps notice that Tom's first bold edit had examples up to 20 vertices, while his second only went up to 15 vertices, and his third (you gave the wrong link, BTW) tried even further to integrate it into the text? His edit summary might say it is a reversion, but it is not. (Try it: if you click "(undo)" on someone else's edit, you can then change the text inside it, thus making it not a complete reversion, but the automatic edit summary will still say it is a complete reversion if it is present.) Double sharp (talk) 11:01, 31 January 2015 (UTC)
- P.S. Now that it's integrated into the text, it doesn't feel like a gallery full of pictures. It instead feels more like one single image giving a few relevant and related examples. Double sharp (talk) 11:05, 31 January 2015 (UTC)
- Thank you for coming over, and sorry about the wrong link. If he triggers an notification and adds an edit comment that I am "picky picky", this bound to inflame. Nor does the modification abrogate the fact that he is warring. I shouldn't need to explicitly point up the bit where we are expected to stop editing while the topic is being discussed. Sure, he has attempted some compromise - a tacit admission that I did have a point after all and was not being picky - but we need to discuss where that line should be drawn, not impose it in battle. I still believe there are too many images but there is no point in attempting serious discussion if I am going to be reverted and insulted at every turn by someone who thinks he WP:OWNS the article because he has "done all the work here". — Cheers, Steelpillow (Talk) 11:28, 31 January 2015 (UTC)
- I apologize for being inflaming in my picky picky, but I'll try to compromise with a mouse as much as an elephant, even if I think both are wrong. Tom Ruen (talk) 11:31, 31 January 2015 (UTC)
- Do you apologise unreservedly for your insulting edit comment or will you continue to insinuate that I am only a mouse-sized problem to you? (I should perhaps caution you that insulting edit comments are particularly frowned on as they stick in the page history and cannot be redacted by the editor concerned). And do you also apologise for warring and undertake not to undo my reverts without first reaching consensus, per WP:BRD? — Cheers, Steelpillow (Talk) 11:47, 31 January 2015 (UTC)
- I apologize for not communicating in a helpful way, nothing more nor less. My mouse comparison was saying I gibve sincere negociation with everyone. And if you know a way I can do a "partial revert" without looking confrontational, I'd like to know. The best way I know how to compromise is by demonstration. Tom Ruen (talk) 12:08, 31 January 2015 (UTC)
- It's very simple to do a partial revert while avoiding confrontation: discuss it on the talk page first, as carefully explained to you at WP:BRD. — Cheers, Steelpillow (Talk) 12:36, 31 January 2015 (UTC)
- Nonsense, a waste of time. My error was not clearly describing my compromise (from 30 down to 13 images) in the revert description. Tom Ruen (talk) 12:39, 31 January 2015 (UTC)
- And you're the one who was breaking the rules with a revert that could have been an edit. Revert an edit if it is not an improvement, and it cannot be immediately fixed by refinement. Tom Ruen (talk) 12:42, 31 January 2015 (UTC)
- Tom, what are you on? You asked "And if you know a way I can do a 'partial revert' without looking confrontational, I'd like to know." So I reminded you of BRD, you reply that BRD is "nonsense" and you already know a better answer, and go back to restoring your images that a third editor had trimmed (see below). — Cheers, Steelpillow (Talk) 12:50, 31 January 2015 (UTC)
- You'll notice Double sharp offered his own compromise, and no one reverted anything. Tom Ruen (talk) 13:04, 31 January 2015 (UTC)
- Tom, what are you on? You asked "And if you know a way I can do a 'partial revert' without looking confrontational, I'd like to know." So I reminded you of BRD, you reply that BRD is "nonsense" and you already know a better answer, and go back to restoring your images that a third editor had trimmed (see below). — Cheers, Steelpillow (Talk) 12:50, 31 January 2015 (UTC)
- It's very simple to do a partial revert while avoiding confrontation: discuss it on the talk page first, as carefully explained to you at WP:BRD. — Cheers, Steelpillow (Talk) 12:36, 31 January 2015 (UTC)
- I apologize for not communicating in a helpful way, nothing more nor less. My mouse comparison was saying I gibve sincere negociation with everyone. And if you know a way I can do a "partial revert" without looking confrontational, I'd like to know. The best way I know how to compromise is by demonstration. Tom Ruen (talk) 12:08, 31 January 2015 (UTC)
- Do you apologise unreservedly for your insulting edit comment or will you continue to insinuate that I am only a mouse-sized problem to you? (I should perhaps caution you that insulting edit comments are particularly frowned on as they stick in the page history and cannot be redacted by the editor concerned). And do you also apologise for warring and undertake not to undo my reverts without first reaching consensus, per WP:BRD? — Cheers, Steelpillow (Talk) 11:47, 31 January 2015 (UTC)
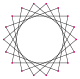
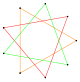
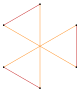
- I've cut it down to eight pictures: 2{3}, 3{3}, 2{4}, 2{5}, 2{5/2}, 3{5/2}, 2{7/2}, and 2{7/3}. I think that ought to be enough for the reader to get the point. (Once the digon pictures are available, I'd consider putting 2{2} and 3{2} in as well, perhaps kicking out the heptagrams.) Double sharp (talk) 11:44, 31 January 2015 (UTC)
- Thank you. I regard the reduction from 30 + 2 to 8 as a great improvement. I'd suggest that only one star compound of digons would be enough, say 3{2}. — Cheers, Steelpillow (Talk) 11:53, 31 January 2015 (UTC)
- I added a row of digon compounds. Trim away as your heart desires, but one example is a sad sad world. Tom Ruen (talk) 13:07, 31 January 2015 (UTC)
- Thank you. I regard the reduction from 30 + 2 to 8 as a great improvement. I'd suggest that only one star compound of digons would be enough, say 3{2}. — Cheers, Steelpillow (Talk) 11:53, 31 January 2015 (UTC)
- I apologize for being inflaming in my picky picky, but I'll try to compromise with a mouse as much as an elephant, even if I think both are wrong. Tom Ruen (talk) 11:31, 31 January 2015 (UTC)
- Thank you for coming over, and sorry about the wrong link. If he triggers an notification and adds an edit comment that I am "picky picky", this bound to inflame. Nor does the modification abrogate the fact that he is warring. I shouldn't need to explicitly point up the bit where we are expected to stop editing while the topic is being discussed. Sure, he has attempted some compromise - a tacit admission that I did have a point after all and was not being picky - but we need to discuss where that line should be drawn, not impose it in battle. I still believe there are too many images but there is no point in attempting serious discussion if I am going to be reverted and insulted at every turn by someone who thinks he WP:OWNS the article because he has "done all the work here". — Cheers, Steelpillow (Talk) 11:28, 31 January 2015 (UTC)