This is an old revision of this page, as edited by 81.153.147.173 (talk) at 03:29, 2 May 2016 (→Sparse autoencoder). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 03:29, 2 May 2016 by 81.153.147.173 (talk) (→Sparse autoencoder)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| Part of a series on |
| Machine learning and data mining |
|---|
| Paradigms |
Problems
|
|
Supervised learning (classification • regression) |
| Clustering |
| Dimensionality reduction |
| Structured prediction |
| Anomaly detection |
| Artificial neural network |
| Reinforcement learning |
| Learning with humans |
| Model diagnostics |
| Mathematical foundations |
| Journals and conferences |
| Related articles |
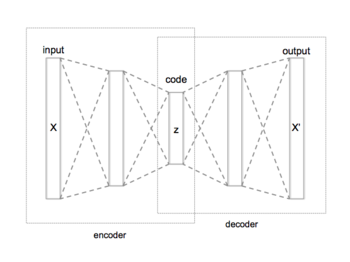
An autoencoder, autoassociator or Diabolo network is an artificial neural network used for learning efficient codings. The aim of an autoencoder is to learn a representation (encoding) for a set of data, typically for the purpose of dimensionality reduction. Recently, the autoencoder concept has become more widely used for learning generative models of data.
Structure
Architecturally, the simplest form of an autoencoder is a feedforward, non-recurrent neural net which is very similar to the multilayer perceptron (MLP), with an input layer, an output layer and one or more hidden layers connecting them. The differences between autoencoders and MLPs, though, are that in an autoencoder, the output layer has the same number of nodes as the input layer, and that, instead of being trained to predict the target value given inputs , autoencoders are trained to reconstruct their own inputs . Therefore, autoencoders are unsupervised learning models.
An autoencoder always consists of two parts, the encoder and the decoder, which can be defined as transitions and , such that:
In the simplest case, where there is one hidden layer, an autoencoder takes the input and maps it onto :
This is usually referred to as code or latent variables (latent representation). Here, is an element-wise activation function such as a sigmoid function or a rectified linear unit. After that, is mapped onto the reconstruction of the same shape as :
Autoencoders are also trained to minimise reconstruction errors (such as squared errors):
If the feature space has less dimensionality than the input space , then the feature vector can be regarded as a compressed representation of the input . If the hidden layers are larger than the input layer, an autoencoder can potentially learn the identity function and become useless. However, experimental results have shown that autoencoders might still learn useful features in these cases.
Variations
Various techniques exist to prevent autoencoders from learning the identity function and to improve their ability to capture important information and learn richer representations.
Denoising autoencoder
Denoising autoencoders take a partially corrupted input whilst training to recover the original undistorted input. This technique has been introduced with a specific approach to good representation. A good representation is one that can be obtained robustly from a corrupted input and that will be useful for recovering the corresponding clean input. This definition contains the following implicit assumptions:
- The higher level representations are relatively stable and robust to the corruption of the input;
- It is necessary to extract features that are useful for representation of the input distribution.
To train an autoencoder to denoise data, it is necessary to perform preliminary stochastic mapping in order to corrupt the data and use as input for a normal autoencoder, with the only exception being that the loss should be still computed for the initial input instead of .
Sparse autoencoder
By imposing sparsity on the hiddern units during training (whilst having a larger number of hidden units than inputs), an autoencoder can learn useful structures in the input data. This allows sparse representations of inputs. These are useful in pretraining for classification tasks.
Sparsity may be achieved by additional terms in the loss function during training (by comparing the probability distribution of the hidden unit activiations with some low desired value), or by manually zeroing all but the few strongest hidden unit activations.
Variational autoencoder (VAE)
Variational autoencoder models inherit autoencoder architecture, but make strong assumptions concerning the distribution of latent variables. They use variational approach for latent representation learning, which results in an additional loss component and specific training algorithm called Stochastic Gradient Variational Bayes (SGVB). It assumes that the data is generated by a directed graphical model and that the encoder is learning an approximation to the posterior distribution where and denote the parameters of the encoder (recognition model) and decoder (generative model). The objective of the variational autoencoder in this case has the following form:
Here, stands for the Kullback–Leibler divergence of the approximate posterior from the prior, and the second term is an expected negative reconstruction error. The prior over the latent variables is set to be the centred isotropic multivariate Gaussian .
Relationship with truncated singular value decomposition (TSVD)
If linear activations are used, or only a single sigmoid hidden layer, then the optimal solution to an autoencoder is strongly related to principal component analysis (PCA), as explained by Pierre Baldi in several papers.
Training
The training algorithm for an autoencoder can be summarized as
- For each input x,
- Do a feed-forward pass to compute activations at all hidden layers, then at the output layer to obtain an output
- Measure the deviation of from the input (typically using squared error),
- Backpropagate the error through the net and perform weight updates.
An autoencoder is often trained using one of the many variants of backpropagation (such as conjugate gradient method, steepest descent, etc.). Though these are often reasonably effective, there are fundamental problems with the use of backpropagation to train networks with many hidden layers. Once errors are backpropagated to the first few layers, they become minuscule and insignificant. This means that the network will almost always learn to reconstruct the average of all the training data. Though more advanced backpropagation methods (such as the conjugate gradient method) can solve this problem to a certain extent, they still result in a very slow learning process and poor solutions. This problem can be remedied by using initial weights that approximate the final solution. The process of finding these initial weights is often referred to as pretraining.
Geoffrey Hinton developed a pretraining technique for training many-layered "deep" autoencoders. This method involves treating each neighboring set of two layers as a restricted Boltzmann machine so that the pretraining approximates a good solution, then using a backpropagation technique to fine-tune the results. This model takes the name of Deep belief network.
References
- ^ Bengio, Y. (2009). "Learning Deep Architectures for AI" (PDF). Foundations and Trends in Machine Learning. 2. doi:10.1561/2200000006.
- Modeling word perception using the Elman network, Liou, C.-Y., Huang, J.-C. and Yang, W.-C., Neurocomputing, Volume 71, 3150–3157 (2008), doi:10.1016/j.neucom.2008.04.030
- Autoencoder for Words, Liou, C.-Y., Cheng, C.-W., Liou, J.-W., and Liou, D.-R., Neurocomputing, Volume 139, 84–96 (2014), doi:10.1016/j.neucom.2013.09.055
- ^ Auto-Encoding Variational Bayes, Kingma, D.P. and Welling, M., ArXiv e-prints, 2013 arxiv
.org /abs /1312 .6114 - Generating Faces with Torch, Boesen A., Larsen L. and Sonderby S.K., 2015 torch
.ch /blog /2015 /11 /13 /gan .html - Vincent, Pascal; Larochelle, Hugo; Lajoie, Isabelle; Bengio, Yoshua; Manzagol, Pierre-Antoine (2010). "Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion". The Journal of Machine Learning Research. 11: 3371–3408.
- sparse autoencoders (PDF)
- k-sparse autoencoder (PDF)
- Bourlard, H.; Kamp, Y. (1988). "Auto-association by multilayer perceptrons and singular value decomposition". Biological Cybernetics. 59 (4–5): 291–294. doi:10.1007/BF00332918. PMID 3196773.
- Baldi et al., "Deep autoencoder neural networks for gene ontology annotation predictions". Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics. ACM, 2014.]
- Reducing the Dimensionality of Data with Neural Networks (Science, 28 July 2006, Hinton & Salakhutdinov)
 given inputs
given inputs  , autoencoders are trained to reconstruct their own inputs
, autoencoders are trained to reconstruct their own inputs  and
and  , such that:
, such that:



 and maps it onto
and maps it onto  :
:

 is an element-wise activation function such as a
is an element-wise activation function such as a  is mapped onto the reconstruction
is mapped onto the reconstruction  of the same shape as
of the same shape as  :
:


 has less dimensionality than the input space
has less dimensionality than the input space  , then the feature vector
, then the feature vector  can be regarded as a
can be regarded as a  . If the hidden layers are larger than the input layer, an autoencoder can potentially learn the
. If the hidden layers are larger than the input layer, an autoencoder can potentially learn the  in order to corrupt the data and use
in order to corrupt the data and use  as input for a normal autoencoder, with the only exception being that the
as input for a normal autoencoder, with the only exception being that the  instead of
instead of  .
.
 and that the encoder is learning an approximation
and that the encoder is learning an approximation  to the
to the  where
where  and
and  denote the parameters of the encoder (recognition model) and decoder (generative model). The objective of the variational autoencoder in this case has the following form:
denote the parameters of the encoder (recognition model) and decoder (generative model). The objective of the variational autoencoder in this case has the following form:

 stands for the
stands for the  .
.