Misplaced Pages

This is an old revision of this page, as edited by Ozob (talk | contribs) at 23:31, 13 March 2010 (→ANI notice: new section). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

I have contributed "Introduction: Basic Principles of Global Positioning" to the GPS article in order to provide a basic understanding of global positioning for the no error case. This will make it easier for the reader to understand the computations required in the presence of errors.RHB100 (talk) 03:26, 27 June 2008 (UTC)

Introduction of Robert H. Biggadike

Hello, I am Robert H. Biggadike. I am a Licensed Professional Engineer in the field of Control System Engineering. I hold advanced engineering degrees from the University of Arkansas and UCLA in addition to an undergraduate engineering degree from Arkansas. In addition to my technical interests, I am interested in libertarianism and capitalism. I am orginally from Newport, Arkansas. I now live in California.

Robert H. Biggadike, Licensed Professional Engineer, Control System Engineering

BSME & MSEM University of Arkansas

Degree of Engineer UCLA (majoring in rigid and elastic body dynamics) RHB100 (talk) 19:43, 28 July 2009 (UTC)

Possible Error in Misplaced Pages Article: GPS

Hi! I replied on my talk page, to keep the discussion in one place. Basically I think you are right and the article has it backwards. This would be a good thing to fix, LouScheffer (talk) 20:12, 27 June 2008 (UTC)

Using the C/A Code

Use ""]" Multidimensional Newton Raphson to link to this target.
Put "<"span id="multi_nr"></span">" in the target.
"" to same article does not work.
<A=HREF="http://en.wikipedia.org/search/?title=User_talk:RHB100&action=edit&section=4#multi_nr">Multi Newton Raphson Test</A> to same article does does not work

I contributed the following paragraph to this section of the GPS article.

When pseudoranges are determined for four satellites, an estimate of the GPS receiver position can be made. Trilateration is used to determine the two points of intersection of three sphere surfaces corresponding to three satellites. The surface of the sphere corresponding to the fourth satellite or the surface of the earth is used to determine which of the two intersections provides a valid estimate of GPS receiver position. The valid estimate is the point closest to the surface of the sphere corresponding to the fourth satellite or the surface of the earth. It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let R4 denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let P4 denote the pseudorange of the fourth satellite. Let DA=R4-P4. Then the quotient, DEL_T= DA/(speed of light), provides an estimate of UTC - (time indicated by the receiver's on-board clock) and the GPS receiver clock can be moved forward if DEL_T is positive or backwards if DEL_T is negative.

Additional Improvements

Improvements desired for "Using the C/A Code" section include adding figures of 2 and 3 spheres intersecting. In this section or possibly in the trilateration article the method of formulating the equations of the spheres in the planar coordinate system required for trilateration should be explained.

Last Version Before Lou Scheffer

When pseudoranges are determined for four satellites, an estimate of the GPS receiver position can be made. Trilateration is used to determine the two points of intersection of three sphere surfaces corresponding to three satellites. The surface of the sphere corresponding to the fourth satellite or the surface of the earth is used to determine which of the two intersections provides a valid estimate of GPS receiver position. The valid estimate is the point closest to the surface of the sphere corresponding to the fourth satellite or the surface of the earth. It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let R4 denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let P4 denote the pseudorange of the fourth satellite. Let DA=R4-P4. Then the quotient, DEL_T= DA/(speed of light), provides an estimate of UTC - (time indicated by the receiver's on-board clock) and the GPS receiver clock can be moved forward if DEL_T is positive or backwards if DEL_T is negative. The above procedure has not taken into account the change in pseudoranges resulting from the correction to the GPS receiver clock. When the magnitude of DEL_T is small this may be adequate. However when DEL_T is large an iterative procedure should be used. The pseudoranges should be recomputed using the updated GPS receiver clock and a new valid estimate of GPS receiver position should be computed as described above. A new value of DEL_T should then be computed. These iterations should be continued until the magnitude of DEL_T is sufficiently small.

Hi! Neither your description, nor mine, describes how GPS receivers actually do the calculation. Furthermore, we both are describing how the pseudoranges are used, and how clock corrections are made. So the main difference is the explanation, I think. My personal description is that equations and variables help little in a case like this - the folks who want equations can derive them from the text, and other who do not want equations or variable definitions do not need to wade through them.

I propose to put both versions on the talk page for GPS, and let others comment. LouScheffer (talk) 02:18, 7 July 2008 (UTC)

To Lou Scheffer: All right, we will see if anything useful can be learned from this. I have used very few equations and the ones that I have are very simple. Variables just provide a name so as to avoid excessive wordiness. ````

TOA (Spheres) is Better than TDOA (Hyperboloids)

There are references to using hyperboloids in the Misplaced Pages GPS article. Analytic Geometry tells us that the locus of points which have a constant difference in distance from two satellite positions lie on a surface called a hyperboloid. Since this surface can be computed based on the difference in time of arrival at the GPS Receiver of messages from different satellites, it suggests that this data would reduce the error due to the GPS Receiver Clock. However judging from GPS literature it seems that spheres based on TOA are used more often. I think there is a good reason for this. It is because you can get a very good clock correction using trilateration with four spheres. This negates the time difference advantage of using hyperboloids in my opinion.RHB100 (talk) 21:39, 9 July 2008 (UTC)

Crazy Software Productions (talk) 19:58, 3 September 2008 (UTC) Using pseudorange calculations (sometimes this is called hyperboloid calculation) can be used for positional calculations. This method converges fast, it is not influenced by the clockerror and with a close first estimate only one iteration is needed. One of the effects of pseudorange calculation is that the the clockerror is also calculated in the process. The solutions I have seen up to now based on spheres have never been complete. The suggested clock correction in the GPS mainarticle is not always in the correct direction and is often far of by amount. So the method described is not a completely working solution. Then the amount of calculation needed is far more than is needed for pseudorange calculations.

Pseudorange calculations converges very fast. An example with (0, 0, 0) (centre of the earth) as a first estimate gave the following 'errors' (this is independend of the timing error):
0 first estimate, error is 6372836 meters
1 first iteration, error is 1718732 meters
2 second iteration, error is 108173 meters
3 third iteration, error is 333 meters
4 fourth iteration, error is 0.002695871 meters (2 millimeters)
5 fifth iteration, error is 2.8 E-9 meters.

So in most situations only one iteration will be sufficient.

The above numbers where calculated using an implementation of the pseudorange calculation in a spreadsheat, only using + - * / and the squareroot. (Spreadsheat is available).

The number of calculations needed for one iteration for the pseudorange calculation can be as low as 69 additions/subtractions, 42 multiplications, 22 divisions and 4 squareroots. Because only one iteration is needed in most situations, this is thus the amount of calculation needed for one positioning. I have not analysed the trilateration but having seen parts of the algoritm I estimate that the amount of calculations for one iteration does exceed the above numbers and the number of iterations needed is larger as wel.

So my conclusion is that TDAO is far better than TOA. Based on the amount of calculation needed and based on the number of iterations needed. (But because I haven't seen the complete algoritm or implementation of TOA a real comparison can not be made). If you can show that TOA does produce better numbers than the above I will be very interrested.

The reason why: "However judging from GPS literature it seems that spheres based on TOA are used more often." Is because this explanes the physics of the GPS system very well. The signals are spread in spheres (and not hyperboloids). And would the signals be timed in such a way that they arrive at the receivers end at the same time, the spheres exactly describe the situation at that point in time. But the picture is draw based on the knowledge where the point of the receiver is. It's much more difficult to explain the process if within that explanation the location of the receiver must be left unknown until the end of the explanation. Where those explanations very often fail is the explaining why a fourth satellite is needed. So sometimes this is described for picking the correct point of two. Or sometimes it is described that it's used to correct the clock. But with pseudorange calculation the whole calculation is based on the information of four satellites, the calculation of the clock error is just one of the results.

Crazy Software Productions (talk) 19:58, 3 September 2008 (UTC)

Basic Concept of GPS

To describe the basic concept of how a GPS receiver works, the errors are at first ignored. Using messages received from four satellites, the GPS receiver is able to determine the satellite positions and time sent. The x, y, and z components of position and the time sent are designated as ${\displaystyle \left}$ where the subscript i denotes which satellite and has the value 1, 2, 3, or 4. Knowing the indicated time the message was received ${\displaystyle \ tr_{i}}$, the GPS receiver can compute the indicated transit time, ${\displaystyle \left(tr_{i}-t_{i}\right)}$. of the message. Assuming the message traveled at the speed of light, c, the distance travelled, ${\displaystyle \ p_{i}}$ can be computed as ${\displaystyle \left(tr_{i}-t_{i}\right)c}$. Knowing the distance from GPS receiver to a satellite and the position of a satellite implies that the GPS receiver is on the surface of a sphere centered at the position of a satellite. Thus we know that the indicated position of the GPS receiver is at or near the intersection of the surfaces of four spheres. In the ideal case of no errors, the GPS receiver will be at an intersection of the surfaces of four spheres. The surfaces of two spheres if they intersect in more than one point intersect in a circle. A figure, Two Sphere Surfaces Intersecting in a Circle, is shown below depicting this which hopefully will aid the reader in visualizing this intersection.

The article, trilateration, shows mathematically how the equation for a circle is determined. A circle and sphere surface in most cases of practical interest intersect at two points, although it is conceivable that they could intersect in 0 or 1 point. Another figure, Surface of Sphere Intersecting a Circle (not disk) at Two Points, is shown below to aid in visualizing this intersection. Again trilateration clearly show this mathematically. The correct position of the GPS receiver is the one that is closest to the fourth sphere. This paragraph has described the basic concept of GPS while ignoring errors. The next problem is how to process the messages when errors are present.

Let ${\displaystyle \ b}$ denote the clock error or bias, the amount by which the receiver's clock is slow. The GPS receiver has four unknowns, the three components of GPS receiver position and the clock bias ${\displaystyle \left}$. The equation of the sphere surfaces are given by:

OLD DESCRIPTION OF TRILATERATION AND TIME ERROR COMPUTATION The above paragraph has provided an overview of the process for computing position and clock correction. For the interested reader this paragraph provides a little more detail on how the spheres intersect, where trilateration is used, the computation of receiver position, clock correction and the iteration process. Utilizing the pseudoranges determined for four satellites, an estimate of the GPS receiver position is made. For the ideal case when the pseudoranges are correct the GPS Receiver must be on the surface of each of the corresponding spheres and therefore must be at one of the intersections of these sphere surfaces. Trilateration is used to determine the two points of intersection of three sphere surfaces corresponding to three satellites. The surface of the sphere corresponding to the fourth satellite or the surface of the earth is used to determine which of the two intersections provides a valid estimate of GPS receiver position. The valid estimate is the point closest to the surface of the sphere corresponding to the fourth satellite or the surface of the earth.

It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let ${\displaystyle \ r_{4}}$ denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let ${\displaystyle \ p_{4}\ }$denote the pseudorange of the fourth satellite. Let ${\displaystyle \ da=r_{4}-p_{4}}$. Note that ${\displaystyle \ da}$ is the distance from the computed GPS receiver position to the surface of the surface of the sphere corresponding to the fourth satellite. Thus the quotient, ${\displaystyle \ b=da/c\ }$, provides an estimate of
(correct time) - (time indicated by the receiver's on-board clock)
and the GPS receiver clock can be moved forward if ${\displaystyle \ b}$ is positive or backwards if ${\displaystyle \ b}$ is negative.

The above procedure has not taken into account the change in pseudoranges resulting from the correction to the GPS receiver clock. When the magnitude of Δt is small this may be adequate. However when Δt is large an iterative procedure should be used. The pseudoranges should be recomputed using the updated GPS receiver clock and a new valid estimate of GPS receiver position should be computed as described above. A new value of Δt should then be computed. These iterations should be continued until the magnitude of Δt is sufficiently small.

Methods of Solution witn No More Than Four Satellites

Two of the most important methods of computing GPS receiver position and clock bias are (1) trilateration followed by one dimensional numerical root finding and (2) multidimensional Newton-Raphson. These two methods along with their advantages are discussed.

• Solve by trilateration followed by one dimensional numerical root finding. This method involves using Trilateration to determine the intersection of the surfaces of three spheres. It is clearly shown in trilateration that the surfaces of three spheres intersect in 0, 1, or 2 points. In the usual case of two intersections, the solution which is nearest the the surface of the sphere corresponding to the fourth satellite is chosen. The surface of the earth can also sometimes be used instead, especially in the case of civilian GPS receivers since it is illegal in the United States to track vehicles of more than 60,000 feet in altitude. The bias, ${\displaystyle \ b}$ is then computed based on the distance from the solution to the surface of the sphere corresponding to the fourth satellite. Using an updated received time based on this bias, new spheres are computed and the process is repeated. One advantage of this method is that it involves one dimensional as opposed to multidimensional numerical root finding.

It is likely the surfaces of the three spheres intersect since the circle of intersection of the first two spheres is normally quite large and thus the third sphere surface is likely to intersect this large circle. It is very unlikely that the surface of the sphere corresponding to the fourth satellite will intersect either of the two points of intersection of the first three since any clock error could cause it to miss intersecting a point. However the distance from the valid estimate of GPS receiver position to the surface of the sphere corresponding to the fourth satellite can be used to compute a clock correction. Let r₄ denote the distance from the valid estimate of GPS receiver position to the fourth satellite and let p₄ denote the pseudorange of the fourth satellite. Let da = r₄ - p₄. Then the quotient, Δt = da / c, provides an estimate of UTC - (time indicated by the receiver's on-board clock) and the GPS receiver clock can be moved forward if Δt is positive or backwards if Δt is negative.

The above procedure has not taken into account the change in pseudoranges resulting from the correction to the GPS receiver clock. When the magnitude of Δt is small this may be adequate. However when Δt is large an iterative procedure should be used. The pseudoranges should be recomputed using the updated GPS receiver clock and a new valid estimate of GPS receiver position should be computed as described above. A new value of Δt should then be computed. These iterations should be continued until the magnitude of Δt is sufficiently small.

• Utilize multidimensional Newton-Raphson. Linearize around an approximate solution say ${\displaystyle \left}$ from iteration k, then solve four linear equations derived from the quadratic equations above to obtain ${\displaystyle \left}$. The radii are large and so the sphere surfaces are close to flat. This near flatness may cause the iterative procedure to converge rapidly in the case where ${\displaystyle \ b}$ is near the correct value and the primary change is in the values of ${\displaystyle x,y,\;and\;z}$, since in this case the problem is merely to find the intersection of nearly flat surfaces and thus close to a linear problem. However when ${\displaystyle \ b}$ is changing significantly, this near flatness does not appear to be advantageous in producing rapid convergence, since in this case these near flat surfaces will be moving as the spheres expand and contract. This possible fast convergence is an advantage of this method. Also it has been claimed that this method is the "typical" method used by GPS receivers.. This disadvantage of this method is that according to , "There are no good general methods for solving systems of more than one nonlinear equations."

• Other methods include: Solve for the intersection of the expanding signals form light cones in 4-space cones, Solve for the intersection of hyperbloids determined by the time difference of signals received from satellites utilizing multilateration, *Solve the equations in accordance with.

Mathematics of Method Involving Multidimensional Newton-Raphson to Solve GPS Equations

Let ${\displaystyle x,y\ and\ z\;}$ denote the true coordinates of GPS receiver position at time, ${\displaystyle \ t}$. Let ${\displaystyle \ b}$ denote the unknown clock error or bias, the amount by which the receiver's clock is slow. Let the coordinates of each satellite, and the time the message was sent, be ${\displaystyle \left}$, let the GPS clock's indicated received time be ${\displaystyle tr_{i}\;for\ i=1,2,3,4}$ and c be the speed of light. The pseudorange is computed as ${\displaystyle p_{i}=\left(tr_{i}-t_{i}\right)c}$. Assume the message travels at the speed of light, then the pseudorange satisfies the equation,

1. :${\displaystyle p_{i}={\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}+(z-z_{i})^{2})}}-bc,\ for\;i=1,2,3,4.}$, When an approximate solution, ${\displaystyle \left}$ rather than the exact solution, ${\displaystyle \left}$ is used in equation 1, there is a residual, ${\displaystyle f_{i}^{(k)}}$. Transforming ${\displaystyle \ p_{i}}$ to the right hand side of the equation there results,
2. :${\displaystyle f_{i}^{(k)}={\sqrt {(x^{(k)}-x_{i})^{2}+(y^{(k)}-y_{i})^{2}+(z^{(k)}-z_{i})^{2})}}-b^{(k)}c-p_{i},\ for\;i=1,2,3,4}$. A solution will have been found when ${\displaystyle f_{i}^{(k)}}$ is zero or sufficiently close to zero for ${\displaystyle \ i=1,2,3,4}$. In order to linearize equation 2 the partial derivatives are computed as
3. ${\displaystyle {\frac {\partial f_{i}^{(k)}}{\partial x^{(k)}}}={\frac {(x^{(k)}-x_{i})}{R_{i}^{(k)}}},{\frac {\partial f_{i}^{(k)}}{\partial y^{(k)}}}={\frac {(y^{(k)}-y_{i})}{R_{i}^{(k)}}},{\frac {\partial f_{i}^{(k)}}{\partial z^{(k)}}}={\frac {(z^{(k)}-z_{i})}{R_{i}^{(k)}}},and\;{\frac {\partial f_{i}^{(k)}}{\partial b^{(k)}}}=-c}$ where ${\displaystyle R_{i}^{(k)}={\sqrt {(x^{(k)}-x_{i})^{2}+(y^{(k)}-y_{i})^{2}+(z^{(k)}-z_{i})^{2})}}}$. Linearizing equation 2 about the apprximate solution, ${\displaystyle \left}$ there results
4. ${\displaystyle f_{i}^{(k)}={\frac {(x^{(k)}-x_{i})}{R_{i}^{(k)}}}x^{(k)}+{\frac {(y^{(k)}-y_{i})}{R_{i}^{(k)}}}y^{(k)}+{\frac {(z^{(k)}-z_{i})}{R_{i}^{(k)}}}z^{(k)}-b^{(k)}c-p_{i}\ for\;i=1,2,3,4.}$. In order to drive ${\displaystyle f_{i}^{(k+1)}}$ closer to zero choose the values ${\displaystyle \left}$ such that
5. ${\displaystyle -f_{i}^{(k)}={\frac {(x^{(k)}-x_{i})}{p_{i}}}(x^{(k+1)}-x^{(k)})+{\frac {(y^{(k)}-y_{i})}{p_{i}}}(y^{(k+1)}-y^{(k)})\;+}$ ${\displaystyle {\frac {(z^{(k)}-z_{i})}{p_{i}}}(z^{(k+1)}-z^{(k)})-(b^{(k+1)}-b^{(k)})c-p_{i}}$. That is choose the values ${\displaystyle \left}$ such that the residual in equation 2 changes by approximately ${\displaystyle \ -f_{i}^{(k)}}$.
   Let ${\displaystyle \Delta x^{(k+1)}\ =\ (x^{(k+1)}-x^{(k)}),\ \Delta y^{(k+1)}\ =\ (y^{(k+1)}-y^{(k)}),\ \Delta z^{(k+1)}\ =\ (z^{(k+1)}-z^{(k)}),\ and}$ ${\displaystyle \Delta b^{(k+1)}\ =\ (b^{(k+1)}-b^{(k)}).}$ Substituting and transposing ${\displaystyle \ p_{i}}$ to the left hand side of the equation, there results
6. ${\displaystyle -f_{i}^{(k)}+p_{i}={\frac {(x^{(k)}-x_{i})}{p_{i}}}\Delta x^{(k+1)}+{\frac {(y^{(k)}-y_{i})}{p_{i}}}\Delta y^{(k+1)}\;+}$ ${\displaystyle {\frac {(z^{(k)}-z_{i})}{p_{i}}}\Delta z^{(k+1)}-\Delta b^{(k+1)}c}$. Equations 6 provide a set of four linear equations in four unknowns, the delta terms. They are in a form for solution. After a solution is found, the ${\displaystyle \left}$ are evaluated using,
7. ${\displaystyle x^{(k+1)}\ =\ x^{(k)}\ +\ \Delta x^{(k+1)},y^{(k+1)}\ =\ y^{(k)}\ +\ \Delta y^{(k+1)},z^{(k+1)}\ =\ z^{(k)}\ +\ \Delta z^{(k+1)}}$, and ${\displaystyle b^{(k+1)}\ =\ b^{(k)}\ +\ \Delta b^{(k+1)}}$. Then set ${\displaystyle \ k=k+1}$ in equations 2 through 6, plug the ${\displaystyle \left}$ from equations 7 into equations 2, set ${\displaystyle \ k=k+1}$ in equations 7, and reevaluate the residuals in equations 2. This procedure is repeated until the residuals are sufficiently small in magnitude.

Extracting Navigation Message Using Demodulation and C/A Gold Code

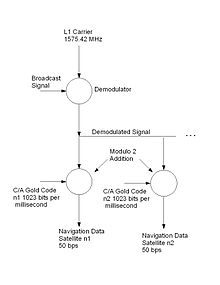
The figure depicts the processing of the signals broadcast by the satellites using the Coarse Acquisition Code. The broadcast signal is demodulated with the 1575.43 MHz L1 carrier. All of the satellite signals are modulated with the L1 carrier. Thus there is a need to separate the signals after demodulation. This is done by modulo 2 addition of the Gold code corresponding to satellite n1, satellite n2, ... nk where k is the number of channels in the GPS receiver. The result of these modulo 2 additions are the 50 bps navigation messages from satellites n1, n2 ... nk. The Gold codes used in GPS are a sequence of 1023 bits with a period of one millisecond. The Gold codes have the property of low cross correlation so that it is unlikely that one satellite signal will be misinterpreted as another. Also the Gold codes have good autocorellation properties.

There are 1025 different Gold codes of length 1023 bits, but only 32 are used. These Gold codes are quite often referred to as pseudo random noise since they contain no message. However, this may be misleading to some readers since they are actually deterministic sequences. Gold_code provides a discusion as does .

Changes of 17 August 2008

Reorganized sections. Moved template to Technical versus Encyclopedic in discussion. Added statements about technical nature of Processing the Navigation Message.

Basic concept of GPS operation

A GPS receiver calculates its position by carefully timing the signals sent by the constellation of GPS satellites high above the Earth. Each satellite continually transmits messages containing the time the message was sent, a precise orbit for the satellite sending the message (the ephemeris), and the general system health and rough orbits of all GPS satellites (the almanac). These signals travel at the speed of light through outer space, and slightly slower through the atmosphere. The receiver uses the arrival time of each message to measure the distance to each satellite, from which it determines the position of the receiver (conceptually the intersection of spheres - see trilateration ) The resulting coordinates are converted to more user-friendly forms such as latitude and longitude, or location on a map, then displayed to the user.

As the reader may have noticed trilateration can result in two solutions.

It is therefore necessary to explain to the reader how this ambiguity can be resolved. There are different methods for accomplishing this.

It might seem that three satellites would be enough to solve for a position, since space has three dimensions. However, a three satellite solution requires the time be known to a nanosecond or so, far better than any non-laboratory clock can provide. Using four or more satellites allows the receiver to solve for time as well as geographical position, eliminating the need for a very accurate clock. In other words, the receiver uses four measurements to solve for four variables: x, y, z, and t. While most GPS applications use the computed location and not the (very accurate) computed time, the time is used in some GPS applications such as time transfer and traffic signal timing.

Although four satellites are required for normal operation, fewer may be needed in some special cases. If one variable is already known (for example, a ship or plane may already know its altitude), a receiver can determine its position using only three satellites. Also, in practice, receivers use additional clues (doppler shift of satellite signals, last known position, dead reckoning, inertial navigation, and so on) to give degraded answers when fewer than four satellites are visible.

A GPS receiver calculates its position by carefully timing the signals sent by the constellation of GPS satellites high above the Earth. Each satellite continually transmits messages containing the time the message was sent, a precise orbit for the satellite sending the message (the ephemeris), and the general system health and rough orbits of all GPS satellites (the almanac). These signals travel at the speed of light through outer space, and slightly slower through the atmosphere. The receiver uses the arrival time of each message to measure the distance to each satellite thereby establishing that the GPS receiver is approximately on the surfaces of spheres centered at each satellite. This information is then used to estimate the position of the GPS receiver as the intersection of sphere surfaces. The resulting coordinates are converted to a more convenient form for the user such as latitude and longitude, or location on a map, then displayed.

It might seem that three satellites would be enough to solve for a position, since space has three dimensions. However it turns out that three spheres usually intersect in two points. Thus the sphere corresponding to the fourth satellite is needed to determine which intersection is the GPS receiver position. Also a fourth satellite is needed to correct the GPS receiver clock by a method which will be described below. While many GPS applications have no particular use for the computed time, it is used in some GPS applications such as time transfer, and it is the only variable of interest in some applications, such as traffic signal timing.

Although four satellites are required for normal operation, fewer may be needed in some special cases. If one variable is already known (for example, a sea-going ship knows its altitude is 0), a receiver can determine its position using only three satellites.

Also, in practice, receivers use additional clues (doppler shift of satellite signals, last known position, dead reckoning, inertial navigation, and so on) to give degraded answers when fewer than four satellites are visible.

article headings

I notice you keep complicating the section headings in Global Positioning System which were quite concise before. Granted, the titles chosen weren't perfect, but changing "Demodulation" to "Demodulation and decoding satellites signals" is excessively verbose. The short form surely hinted sufficiently at the section's subtopic. See WP:HEAD which references WP:MOS#Article titles.2C headings and sections which prefers short section names. —EncMstr (talk) 21:42, 22 August 2008 (UTC)

I was trying to save you some reading, but since you didn't see the headings and sections portion, you should just read all of the Manual of Style. Either that, or read some featured articles and you'll see that brevity is valued. Here are some good examples of technical articles: HTTP cookie, Search engine optimization, Automatic number plate recognition, Plug-in hybrid, and Construction of the World Trade Center. —EncMstr (talk) 01:48, 23 August 2008 (UTC)

Picking one of two solutions

Hi!

You seem very sure that one of the uses of the fourth satellite is to pick among one of two solutions. But I think this is (almost) never needed, and never used in practice, since the two solutions are always widely separated, with only one near the Earth's surface. If you can find a technical reference that shows that any GPS receivers do this (other than perhaps some specialized receivers for use in deep outer space), I'll be very surprised. Otherwise I think we should state the method of disambiguation that is really used, and not a theoretical use.

This is part of a more general comment. There is a very fine line between a simplified explanation, and an explanation simplified so far it is not longer correct, and could mislead the reader. My personal belief is that we should err on the side of a correct explanation, and not talk down to the reader. This is because one of the main targets is someone who wants to learn more, and they should not find that the detailed information contradicts the simple stuff they read first. Such contradictions make them suspicious of the information as a whole... LouScheffer (talk) 12:15, 24 August 2008 (UTC)

Hi, The 3 satellite solutions you referenced works by assuming 0 altitude, not by assuming an accurate clock. This would give very bad results in practice. It also explains why 4 are needed to determine altitude - with 3 they just assume the altitude is 0. This page also says: "But more to the point, using only three satellites inevitably involves timing error that leads to inaccurate measurements. If you add a fourth satellite, its sphere will not intersect at the same point as the other three. That permits the receiver to figure out the timing error and factor it into the calculations of the other spheres." This I think reinforces the point that the main (and in practice only) reason for satellite 4 is to reduce clock errors. LouScheffer (talk) 20:36, 25 August 2008 (UTC)

Demodulation and decoding

Since all of the satellite signals are modulated onto the same L1 carrier frequency, there is a need to separate the signals after demodulation. This is done by assigning each satellite a unique pseudorandom sequence known as a Gold code, and the signals are decoded, after demodulation, using modulo 2 addition of the Gold codes corresponding to satellites n₁ through n_k, where k is the number of channels in the GPS receiver and n₁ through n_k are the pseudorandom numbers associated with the satellites. The result of these modulo 2 additions are the 50 bps navigation messages from satellites n₁ through n_k. The Gold codes used in GPS are a sequence of 1023 bits with a period of one millisecond. These Gold codes are highly mutually orthogonal, so that it is unlikely that one satellite signal will be misinterpreted as another. As well, the Gold codes have good auto-correlation properties..

There are 1025 different Gold codes of length 1023 bits, but only 32 are used. These Gold codes are quite often referred to as "pseudo-random noise" since they contain no data. However, this may be misleading since they are actually deterministic sequences.

If the almanac information has previously been acquired, the receiver picks which satellites to listen for by their PRN numbers. If the almanac information is not in memory, the receiver enters a search mode and cycles through the PRN numbers until a lock is obtained on one of the satellites. To obtain a lock, it is necessary that there be an unobstructed line of sight from the receiver to the satellite. The receiver can then acquire the almanac and determine the satellites it should listen for. As it detects each satellite's signal, it identifies it by its distinct C/A code pattern.

For each sattelite to which it listens, the receiver must calculate the time the message was sent. Transmission of each 30 second navigation message frame begins precisely on the minute or half minute as indicated by the satellite's atomic clock according to Satellite message format. In particular the first frame of every navigation message begins precisely on the minute or half minute indicated by the satellite atomic clock. Correcting these times by satellite's clock offset previously obtained gives a set of times differing by 30 seconds at which time the message was sent according to receiver clock. Since 30 seconds corresponds to a distance of about 9 million kilometers, the receiver can select which one corresponds to the time at which the message was sent.

The receiver also measures the received time for each satellite. As a first step in doing this, the receiver uses the C/A Gold code with the same PRN number as the satellite to compute an offset from the time sent that generates the best correlation. Call this offset, O. The true offset giving the best estimate of message transit time differs from O by an approximately integral number of milliseconds since the satellite repeats the broadcast of the PRN sequence each millisecond. The offset, O, is computed in a trial and error manner. The 1023 bits of the satellite PRN signal are compared with the receiver PRN signal. If correlation is not achieved, the 1023 bits of the sattelite PRN signal is shifted by one bit relative to the receiver PRN signal and again compared with this signal. This process is repeated until correlation is achieved.

Since the carrier frequncy received can vary due to Doppler, the points where received PRN sequences begin may not differ from O by an exact integral number of milliseconds. Because of this, carrier frequncy tracking along with PRN code phase tracking are used to determine the points in time where the beginning of received satellite PRN code begins. As the receiver continues to read successive PRN sequences, it will encounter a sudden change in phase of the 1023 bit received PRN signal. This indicates the beginning of a data bit of the navigation message. This enables the receiver to begin reading the 20 millisecond bits of the navigation message. Each subframe of the navigation frame begins with a Telemetry Word which enables the receiver to detect the beginning of a subframe. Also each subframe of the navigation frame is identified by bits in the Handover Word (HOW) thereby enabling the receiver to determine which subframe NAVSTAR GPS USER EQUIPMENT INTRODUCTION Chapter 1. Thus upon reading this information, the receiver can begin interpreting the navigation message.

Next the clock adjustment data in the navigation message is used to recalculate the time sent. Then the orbital position data, or ephemeris, from the Navigation Message is used to calculate precisely where the satellite was at the start of the message. A more sensitive receiver will potentially acquire the ephemeris data more quickly than a less sensitive receiver, especially in a noisy environment.

This computation of sent time, received time, etc. is repeated for each satellite to which the receiver listens.

Basic concept of GPS

A GPS receiver calculates its position by carefully timing the signals sent by the constellation of GPS satellites high above the Earth. Each satellite continually transmits messages containing the time the message was sent, precise orbital information (the ephemeris), and the general system health and rough orbits of all GPS satellites (the almanac). These signals travel at the speed of light. The receiver measures the transit time of each message and uses these transit times along with the speed of light to compute the distance to each satellite. These distances are used to compute two estimates of receiver positions (conceptually the intersection of sphere surfaces—see trilateration). It uses additional known information, such as being on board a near Earth vehicle, to determine which of the two is the valid estimate of position. The receiver clock is then corrected as discussed below to get a much more accurate estimate of position. The final calculated position is displayed as

1) latitude, longitude, and possibly altitude or

2) location on a map and possibly altitude.

It might seem that three satellites would be enough to solve for a position, since space has three dimensions. However, a three-satellite solution requires that time be known to a nanosecond or so—far more accurate than a non-laboratory clock provides. Using four (or more) satellites allows the receiver to solve for time as well as geographical position, eliminating the need for a very accurate clock. In other words, the receiver uses four measurements to solve for four variables: x, y, z, and t. While most GPS applications use the computed location only and effectively hide the very accurately computed time, the time is used in a few GPS applications such as time transfer and traffic signal timing.

Although four satellites are required for normal operation, fewer may be needed in special cases. If one variable is already known (for example, a ship or plane may have known elevation), a receiver can determine its position using only three satellites. Some GPS receivers may use additional clues or assumptions (such as re-using the last known altitude, dead reckoning, inertial navigation, or including information from the vehicle computer) to give degraded answers when fewer than four satellites are visible.

Phase and Frequency Tracking

Since the carrier frequency received can vary due to Doppler shift, the points where received PRN sequences begin may not differ from O by an exact integral number of milliseconds. Because of this, carrier frequency tracking along with PRN code tracking are used to determine when the received satellite's PRN code begins (see "How a GPS Receiver Gets a Lock"). Unlike the earlier computation of offset in which trial of all 1023 offset could potentially be required, the tracking to maintain lock usually requires shifting of one pulse width or less. To perform this tracking, the receiver observes two quantities, phase error and received frequency offset. The correlation of the received PRN code with respect to the receiver generated PRN code is computed to determine if the bits of the two signals are misaligned. Comparison with correlation computed with receiver generated PRN code shifted slightly forward and slightly backward are used to estimate adjustment required. The amount of adjustment required for maximum correlation is used in estimating phase error. Received frequency offset from the frequency generated by the receiver provides an estimate of phase rate error. The command for the frequency generator and any further PRN code shifting required are computed as a function of the phase error and the phase rate error in accordance with the control law used. The Doppler velocity is computed as a function of the difference of the frequency offset from the carrier nominal frequency. The Doppler velocity is the velocity component along the line of sight of the receiver relative to the satellite.

according to

, Chapters 7 and 8 of

and

.

Geometric dilution of precision computation (DOP)

As a first step n computing DOP, consider the unit vectors from the receiver to satellite i.

${\displaystyle {\frac {(x_{i}-x)}{R_{i}}},{\frac {(y_{i}-y)}{R_{i}}},and{\frac {(z_{i}-z)}{R_{i}}}}$ where

${\displaystyle R_{i}={\sqrt {(x_{i}-x)^{2}+(y_{i}-y)^{2}+(z_{i}-z)^{2}}}}$ and where ${\displaystyle \ x,y,and\ z}$ denote the position of the receiver and ${\displaystyle \ x_{i},y_{i},and\ z_{i}}$ denote the position of satellite i. Formulate the matrix A as

${\displaystyle A={\begin{bmatrix}{\frac {(x_{1}-x)}{R_{1}}}&{\frac {(y_{1}-y)}{R_{1}}}&{\frac {(z_{1}-z)}{R_{1}}}&c\\{\frac {(x_{2}-x)}{R_{2}}}&{\frac {(y_{2}-y)}{R_{2}}}&{\frac {(z_{2}-z)}{R_{2}}}&c\\{\frac {(x_{3}-x)}{R_{3}}}&{\frac {(y_{3}-y)}{R_{3}}}&{\frac {(z_{3}-z)}{R_{3}}}&c\\{\frac {(x_{4}-x)}{R_{4}}}&{\frac {(y_{4}-y)}{R_{4}}}&{\frac {(z_{4}-z)}{R_{4}}}&c\end{bmatrix}}}$

The first three elements of each row of A are the components of a unit vector from the receiver to the indicated satellite. The elements in the fourth column are c where c denotes the speed of light. Formulate the matrix, Q, as

${\displaystyle Q=\left(A^{T}A\right)^{-1}}$

This computation is in accordance with "Section 1.4.2 of PRINCIPLES OF SATELLITE POSITIONING" where the weighting matrix, P, has been set to the identity matrix.

The elements of the Q matrix are designated as

${\displaystyle Q={\begin{bmatrix}d_{x}^{2}&d_{xy}^{2}&d_{xz}^{2}&d_{xt}^{2}\\d_{xy}^{2}&d_{y}^{2}&d_{yz}^{2}&d_{yt}^{2}\\d_{xz}^{2}&d_{yz}^{2}&d_{z}^{2}&d_{zt}^{2}\\d_{xt}^{2}&d_{yt}^{2}&d_{zt}^{2}&d_{t}^{2}\end{bmatrix}}}$

The Greek letter ${\displaystyle \sigma }$ is used quite often where we have used d. However the elements of the Q matrix do not represent variances and covariances as they are defined in probability and statistics. Instead they are strictly geometric terms. Therefore d as in dilution of precision is used. PDOP, TDOP and GDOP are given by

${\displaystyle PDOP={\sqrt {d_{x}^{2}+d_{Y}^{2}+d_{Z}^{2}}}}$,

${\displaystyle \ TDOP={\sqrt {d_{t}^{2}}}}$, and

${\displaystyle GDOP={\sqrt {PDOP^{2}+TDOP^{2}}}}$ in agreement with "Section 1.4.9 of PRINCIPLES OF SATELLITE POSITIONING".

The horizontal dilution of precision, ${\displaystyle HDOP={\sqrt {d_{x}^{2}+d_{Y}^{2}}}}$, and the vertical dilution of precision, ${\displaystyle \ VDOP={\sqrt {d_{z}^{2}}}}$, are both dependent on the coordinate system used. To correspond to the local horizon plane and the local vertical, x, y, and z should denote positions in either a North, East, Down coordinate system or a South, East, Up coordinate system.RHB100 (talk) 22:36, 11 December 2008 (UTC)

Derivation of DOP Equations

The equations for computing the geometric dilution of precision terms has been described in the previous section. This section describes the derivation of these equations. The method used here is similar to that used in "Global Positioning System (preview) by Parkinson and Spiker"

Consider the position error vector, e, defined as the vector from the indicated postion to the true position of the receiver.  :${\displaystyle \mathbf {e} =e_{x}{\hat {x}}+e_{y}{\hat {y}}+e_{z}{\hat {z}}}$ where bold denotes a vector and ${\displaystyle {\hat {x}},\ {\hat {y}},\ and\ {\hat {z}}}$ denote unit vectors along the x, y, and z axes respectively. Let ${\displaystyle \ e_{t}}$ denote the time error, the true time minus the receiver indicated time. Assume that the mean value of the three components of e and ${\displaystyle \ e_{t}}$ are zero.

${\displaystyle A\ {\begin{bmatrix}e_{x}\\e_{y}\\e_{z}\\e_{t}\end{bmatrix}}={\begin{bmatrix}{\frac {(x_{1}-x)}{R_{1}}}&{\frac {(y_{1}-y)}{R_{1}}}&{\frac {(z_{1}-z)}{R_{1}}}&c\\{\frac {(x_{2}-x)}{R_{2}}}&{\frac {(y_{2}-y)}{R_{2}}}&{\frac {(z_{2}-z)}{R_{2}}}&c\\{\frac {(x_{3}-x)}{R_{3}}}&{\frac {(y_{3}-y)}{R_{3}}}&{\frac {(z_{3}-z)}{R_{3}}}&c\\{\frac {(x_{4}-x)}{R_{4}}}&{\frac {(y_{4}-y)}{R_{4}}}&{\frac {(z_{4}-z)}{R_{4}}}&c\end{bmatrix}}\ {\begin{bmatrix}e_{x}\\e_{y}\\e_{z}\\e_{t}\end{bmatrix}}={\begin{bmatrix}e_{1}\\e_{2}\\e_{3}\\e_{4}\end{bmatrix}}\ (1)\ where\ e_{1},\ e_{2},\ e_{3},\ and\ e_{4}}$ are the errors in pseudoranges 1 through 4 respectively. This equation comes from linearizing the equation relating pseudoranges to receiver position, satellite positions, and receiver clock errors as shown in .

Multiplying both sides by ${\displaystyle \ A^{-1}\ }$ there results

${\displaystyle \ {\begin{bmatrix}e_{x}\\e_{y}\\e_{z}\\e_{t}\end{bmatrix}}=A^{-1}{\begin{bmatrix}e_{1}\\e_{2}\\e_{3}\\e_{4}\end{bmatrix}}\ (2)}$ . Transposing both sides

${\displaystyle \ {\begin{bmatrix}e_{x}&e_{y}&e_{z}&e_{t}\end{bmatrix}}={\begin{bmatrix}e_{1}&e_{2}&e_{3}&e_{4}\end{bmatrix}}\left(A^{-1}\right)^{T}\ (3)}$ .

Post multiplying the matrices on both sides of equation (2) by the corresponding matrices in equation (3), there results

${\displaystyle \ {\begin{bmatrix}e_{x}\\e_{y}\\e_{z}\\e_{t}\end{bmatrix}}{\begin{bmatrix}e_{x}&e_{y}&e_{z}&e_{t}\end{bmatrix}}=A^{-1}{\begin{bmatrix}e_{1}\\e_{2}\\e_{3}\\e_{4}\end{bmatrix}}{\begin{bmatrix}e_{1}&e_{2}&e_{3}&e_{4}\end{bmatrix}}\left(A^{-1}\right)^{T}\ (4)}$ .

Taking the expected value of both sides and taking the non-random matrtices outside the expectation operator, E, there results

${\displaystyle \ E\left({\begin{bmatrix}e_{x}\\e_{y}\\e_{z}\\e_{t}\end{bmatrix}}{\begin{bmatrix}e_{x}&e_{y}&e_{z}&e_{t}\end{bmatrix}}\right)=A^{-1}\ E\left({\begin{bmatrix}e_{1}\\e_{2}\\e_{3}\\e_{4}\end{bmatrix}}{\begin{bmatrix}e_{1}&e_{2}&e_{3}&e_{4}\end{bmatrix}}\right)\left(A^{-1}\right)^{T}\ (5)}$ .

Assuming the pseudorange errors are uncorrelated and have the same variance, the covariance matrix on the right side can be expressed as a scalar times the identity matrix. Thus

${\displaystyle {\begin{bmatrix}\sigma _{x}^{2}&\sigma _{xy}^{2}&\sigma _{xz}^{2}&\sigma _{xt}^{2}\\\sigma _{xy}^{2}&\sigma _{y}^{2}&\sigma _{yz}^{2}&\sigma _{yt}^{2}\\\sigma _{xz}^{2}&\sigma _{yz}^{2}&\sigma _{z}^{2}&\sigma _{zt}^{2}\\\sigma _{xt}^{2}&\sigma _{yt}^{2}&\sigma _{zt}^{2}&\sigma _{t}^{2}\end{bmatrix}}=\sigma _{R}^{2}\ A^{-1}\left(A^{-1}\right)^{T}=\sigma _{R}^{2}\ \left(A^{T}A\right)^{-1}\ (6)\ since\ A^{-1}\left(A^{-1}\right)^{T}\left(A^{T}A\right)=I}$

${\displaystyle \ Note:\left(A^{-1}\right)^{T}=\left(A^{T}\right)^{-1}\ since\ I=\left(AA^{-1}\right)^{T}=\left(A^{-1}\right)^{T}A^{T}}$

Substituting for ${\displaystyle \left(A^{T}A\right)^{-1}=Q}$ there follows

${\displaystyle {\begin{bmatrix}\sigma _{x}^{2}&\sigma _{xy}^{2}&\sigma _{xz}^{2}&\sigma _{xt}^{2}\\\sigma _{xy}^{2}&\sigma _{y}^{2}&\sigma _{yz}^{2}&\sigma _{yt}^{2}\\\sigma _{xz}^{2}&\sigma _{yz}^{2}&\sigma _{z}^{2}&\sigma _{zt}^{2}\\\sigma _{xt}^{2}&\sigma _{yt}^{2}&\sigma _{zt}^{2}&\sigma _{t}^{2}\end{bmatrix}}=\sigma _{R}^{2}\ {\begin{bmatrix}d_{x}^{2}&d_{xy}^{2}&d_{xz}^{2}&d_{xt}^{2}\\d_{xy}^{2}&d_{y}^{2}&d_{yz}^{2}&d_{yt}^{2}\\d_{xz}^{2}&d_{yz}^{2}&d_{z}^{2}&d_{zt}^{2}\\d_{xt}^{2}&d_{yt}^{2}&d_{zt}^{2}&d_{t}^{2}\end{bmatrix}}\ (7)}$

From equation (7), it follows that the variances of indicated receiver position and time are

${\displaystyle \sigma _{rc}^{2}=\sigma _{x}^{2}+\sigma _{y}^{2}+\sigma _{z}^{2}=\sigma _{R}^{2}\left(d_{x}^{2}+d_{y}^{2}+d_{z}^{2}\right)=PDOP^{2}\sigma _{R}^{2}}$ and

${\displaystyle \sigma _{t}^{2}=\sigma _{R}^{2}d_{t}^{2}=TDOP^{2}\sigma _{R}^{2}}$ .

The remaining position and time error variance terms follow in a straightforward manner.

Carrier phase tracking (surveying)

Utilizing the navigation message to measure pseudorange has been discussed. Another method that is used in GPS surveying applications is carrier phase tracking. The period of the carrier frequency times the speed of light gives the wave length, which is about 0.19 meters for the L1 carrier. With a 1% of wave length accuracy in detecting the leading edge, this component of pseudorange error might be as low as 2 millimeters. This compares to 3 meters for the C/A code and 0.3 meters for the P code.

However, this 2 millimeter accuracy requires measuring the total phase, that is the total number of wave lengths plus the fractional wavelength. This requires specially equipped receivers. This method has many applications in the field of surveying.

We now describe a method which could potentially be used to estimate the position of receiver 2 given the position of receiver 1 using triple differencing followed by a mathematical technique called least squares. A detailed discussion of the errors is omitted in order to avoid detracting from the description of the methodology. In this description differences are taken in the order of differencing between satellites, differencing between receivers, and differencing between epochs. This should not be construed to mean that this is the only order which can be used. Indeed other orders of taking differences are equally valid.

The satellite carrier total phase can be measured with ambiguity as to the number of cycles as described in CARRIER PHASE MEASUREMENT and CARRIER BEAT PHASE. Let ${\displaystyle \ \phi (r_{i},s_{j},t_{k})}$ denote the phase of the carrier of satellite j measured by receiver i at time ${\displaystyle \ t_{k}}$. This notation has been chosen so as to make it clear what the subscripts i, j, and k mean. In view of the fact that the receiver, satellite, and time come in alphabetical order as arguments of ${\displaystyle \ \phi }$ and to strike a balance between readability and conciseness, let ${\displaystyle \ \phi _{i,j,k}=\phi (r_{i},s_{j},t_{k})}$ so as to have a concise abbreviation. Also we define a three functions, :${\displaystyle \ \Delta ^{r},\Delta ^{s},and\Delta ^{t}}$ which perform differences between receivers, satellites, and time points respectively. Each of these functions has a linear combination of three subscripted variable as its argument. These three functions are defined with the following six equations.

${\displaystyle \ \Delta ^{r}(\alpha _{i,j,k})=\alpha _{i+1,j,k}-\alpha _{i,j,k}}$ ,

${\displaystyle \ \Delta ^{s}(\alpha _{i,j,k})=\alpha _{i,j+1,k}-\alpha _{i,j,k}}$ ,

${\displaystyle \ \Delta ^{t}(\alpha _{i,j,k})=\alpha _{i,j,k+1}-\alpha _{i,j,k}}$ . and also

${\displaystyle \ \Delta ^{r}(\alpha _{i,j,k}\pm \beta _{l,m,n})=\Delta ^{r}(\alpha _{i,j,k})\pm \Delta ^{r}(\beta _{l,m,n})}$ ,

${\displaystyle \ \Delta ^{s}(\alpha _{i,j,k}\pm \beta _{l,m,n})=\Delta ^{s}(\alpha _{i,j,k})\pm \Delta ^{s}(\beta _{l,m,n})}$ ,

${\displaystyle \ \Delta ^{t}(\alpha _{i,j,k}\pm \beta _{l,m,n})=\Delta ^{t}(\alpha _{i,j,k})\pm \Delta ^{t}(\beta _{l,m,n})}$ ,

Receiver clock errors can be approximately eliminated by differencing the phases measured from satellite 1 with that from satellite 2 at the same epoch as shown in BETWEEN-SATELLITE DIFFERENCING. This difference is designated as ${\displaystyle \ \Delta ^{s}(\phi _{1,1,1})=\phi _{1,2,1}-\phi _{1,1,1}}$

Double differencing can be performed by taking the differeces of the between satellite difference observed by receiver 1 with that observed by receiver 2. The satellite clock errors will be approximately eliminated by this between receiver differencing. This double difference is designated as ${\displaystyle \ \Delta ^{r}(\Delta ^{s}(\phi _{1,1,1})=\Delta ^{r}(\phi _{1,2,1}-\phi _{1,1,1})}$ .

Triple differencing can be performed by taking the difference of double differencing performed at time ${\displaystyle \ t_{2}}$ with that performed at time ${\displaystyle \ t_{1}}$. This will eliminate the ambiguity associated with the integral number of wave lengths in carrier phase provided this ambiguity does not change with time. Thus the triple difference result has eliminated all or practically all clock bias errors and the integer ambiguity. Also errors associated with atmospheric delay and satellite ephemeris have been significantly reduced. This triple difference is designated as ${\displaystyle \ \Delta ^{t}(\Delta ^{r}(\Delta ^{s}(\phi _{1,1,1})))}$ .

Triple difference results can be used to estimate unknown variables. For example if the position of receiver 1 is known but the position of receiver 2 unknown, it may be possible to estimate the position of receiver 2 using least squares. Although the errors in the triple difference results have been reduced there is still some residual error. Thus triple differencing should be performed at several time pairs to increase estimate accuracy. This will result in an over determined system. To get estimates for an over determined system, least squares can be used. The least squres procedure determines the position of receiver 2 which best fits the observed triple differences under the criterion of minimizing the sum of the squares of the differences between the measured triple differences and the triple differences computed with the estimated position of receiver 2.

References

1. ^ Press, Flannery, Tekolsky, and Vetterling 1986, Numerical Recipes, The Art of Scientific Computing (Cambridge University Press).
2. Noe, P.S.; Myers, K.A. (March 1976). "A Position Fixing Algorithm for the Low-Cost GPS Receiver". IEEE Transactions on Aerospace and Electronic Systems. AES-12 (2): 295–297.{{cite journal}}: CS1 maint: multiple names: authors list (link)
3. Template:Cite article
4. Jay Farrell, Matthew Barth (1999). The global positioning system and inertial navigation. McGraw-Hill. ISBN 007022045X., p. 145.
5. Bancroft, S. (1985). "An Algebraic Solution of the GPS Equations". Aerospace and Electronic Systems, IEEE Transactions on: 56--59.
6. Krause, L.O. (1987). "A Direct Solution to GPS-Type Navigation Equations". Aerospace and Electronic Systems, IEEE Transactions on. AES-23 (2): 225–232. doi:10.1109/TAES.1987.313376. {{cite journal}}: Unknown parameter |month= ignored (help)
7. "[George, M., Hamid, M., and Miller A. Template:PDFlink
8. "GPS - explained (Signals)"
9. HowStuffWorks: How GPS Receivers WorkAccessed May 14, 2006.
10. Georg zur Bonsen, Daniel Ammann, Michael Ammann, Etienne Favey, Pascal Flammant (2005-04-01). "Continuous Navigation Combining GPS with Sensor-Based Dead Reckoning". GPS World.{{cite web}}: CS1 maint: multiple names: authors list (link)
11. "NAVSTAR GPS USER EQUIPMENT INTRODUCTION" (PDF). US Government., Chapters 7 and 8.
12. "GPS Support Notes" (PDF).
13. "[George, M., Hamid, M., and Miller A. Template:PDFlink
14. "AN02 Network Assistance" (HTML). Retrieved 2007-09-10.
15. The speed of light varies slightly between the partial vacuum of space and the denser atmosphere, however a receiver can approximate these effects. Once a rough position is determined, some receivers carefully compute the amount of atmosphere the signal traveled through and adjust the signal timing accordingly.
16. HowStuffWorks: How GPS Receivers Work accessed May 14, 2006.
17. The (usually erroneous)second position is typically tens of thousands of miles above the earth.
18. Georg zur Bonsen, Daniel Ammann, Michael Ammann, Etienne Favey, Pascal Flammant (2005-04-01). "Continuous Navigation Combining GPS with Sensor-Based Dead Reckoning". GPS World.{{cite web}}: CS1 maint: multiple names: authors list (link)
19. "NAVSTAR GPS USER EQUIPMENT INTRODUCTION" (PDF). US Government., Chapters 7 and 8.
20. "GPS Support Notes" (PDF).
21. Georg zur Bonsen, Daniel Ammann, Michael Ammann, Etienne Favey, Pascal Flammant (2005-04-01). "Continuous Navigation Combining GPS with Sensor-Based Dead Reckoning". GPS World.{{cite web}}: CS1 maint: multiple names: authors list (link)
22. "NAVSTAR GPS USER EQUIPMENT INTRODUCTION" (PDF). US Government.
23. "GPS Support Notes" (PDF). January 19, 2007. Retrieved 2008-11-10.

G-force

Remove-This commonly used term is a common error. An encyclopedia should not repeat common misconceptions. G-force was not natural to Isaac Newton who regarded force and acceleration as two completely different things.

Robert H. Biggadike, Licensed Professional Engineer, Control System Engineering

BSME & MSEM University of Arkansas

Degree of Engineer UCLA (majoring in rigid and elastic body dynamics) RHB100 (talk) 19:51, 28 July 2009 (UTC)

You have placed a Dubious on G-force but no arguement. Would you like to open discussion? Is your point the statement above? If so how do we handle the fact that the term is in almost universal usage, and not just by laypeople? We cannot say it doen't exist. It is valid and useful to say my airplane is certified to +6g/-3g, it's even got a g recorder to measure it. Ex nihil (talk) 23:58, 4 August 2009 (UTC)

Re: Why is PRN 08 not listed in article, List of GPS satellite launches

Because I couldn't find it in the first pass. It's in there now. --  Denelson83  23:37, 17 August 2009 (UTC)

If ice did not float, bodies of water would freeze from the bottom to the top - Unjustified Speculation

If ice did not float, bodies of water would freeze from the bottom toward the top. Sinking ice brings about two effects at the surface. (1) An increased temperature difference between the water and the atmosphere due to warmer water replacing the sinking ice. This effect would cause greater heat transfer from the water to the atmosphere. (2) A reduction of thermal conductivity across the layer formerly occupied by the ice since as shown in Selected properties of fresh water, the thermal conductivity of water is lower than that of ice by almost a factor of four near freezing temperature. This effect would cause the heat flow from the water to the atmosphere to decrease. If the former effect is predominant then there will be an increased heat flow from the surface to the atmosphere. If it is also assumed that any change in the heat flow from the earth into the body of water as a result of the ice falling to the bottom is small compared to the heat transfer at the surface then in accordance with the First law of thermodynamics, there would be increased cooling of the body of water under the condition of ice sinking over the condition of reality, floating ice. Thus under these assumptions, freezing from the bottom all the way to the top would be more likely if ice did not float.

This freezing of the body of water could kill fish and other creatures not resistant to freezing temperatures. Density of ice increases slightly with decreasing temperature and has a value of 0.9340 g/cm³ at −180 °C (93 K).

Cross reference of PRN's to Blocks

Geoid non-rotating gravitational potential in progress

From the vector diagram, using bold to denote vectors it follows that

R = r1 + r ,

r = R - r1 , and

r = |R - r1| . Squaring and then taking the square root,

r = ${\displaystyle {\sqrt {R^{2}-2\mathbf {R\cdot r1} +r1^{2}}}\ .}$ Factoring out R.

r = ${\displaystyle R{\sqrt {1-{\frac {2\mathbf {R\cdot r1} }{R^{2}}}+\left({\frac {r1}{R}}\right)^{2}}}\ .}$ Since we are interested in the case in which r > 0, we can invert both sides to get

${\displaystyle r^{-1}=R^{-1}\left(1-{\frac {2\mathbf {R\cdot r1} }{R^{2}}}+\left({\frac {r1}{R}}\right)^{2}\right)^{-{\frac {1}{2}}}\ .}$

${\displaystyle r^{-1}=R^{-1}\left(1-2cos(b){\frac {r1}{R}}+\left({\frac {r1}{R}}\right)^{2}\right)^{-{\frac {1}{2}}}\ .}$

Consider the function,

${\displaystyle f(x)=\left(1-2cos(b)x+x^{2}\right)^{-{\frac {1}{2}}}\ .}$

${\displaystyle f'(x)=\left(cos(b)-x\right)\left(1-2cos(b)x+x^{2}\right)^{-{\frac {3}{2}}}\ .}$

${\displaystyle f''(x)=-\left(1-2cos(b)x+x^{2}\right)^{-{\frac {3}{2}}}}$ ${\displaystyle +3\left(cos(b)-x\right)^{2}\left(1-2cos(b)x+x^{2}\right)^{-{\frac {5}{2}}}\ .}$

Expanding f(x) in a Taylor series about x = 0, we get,

${\displaystyle f(x)=1+x\ cos(b)+x^{2}{\frac {3cos(b)^{2}-1}{2}}+\ ...\ .\ }$ Utilizing the definition of Legendre Polynomials we get,

${\displaystyle f(x)=P_{0}(cos(b))+x\ P_{1}(cos(b))+x^{2}\ P_{2}(cos(b))+\ ...\ }$ where the ${\displaystyle \ P_{n}(cos(b))}$ are Legendre Polynomials of order n with argument, cos(b). The appearance of the first three terms of the series for f(x) suggests that the infinite series might be of similar form. On page 454 of AEM by C. R. Wylie, Jr., Theorem 2 which states that ${\displaystyle \left(1-2XZ+Z^{2}\right)^{-{\frac {1}{2}}}\ =\sum _{n=0}^{\infty }Z^{n}P_{n}(X)\ }$, is proven. Applied to the notation used here Theorem 2 states that ${\displaystyle \left(1-2cos(b)x+x^{2}\right)^{-{\frac {1}{2}}}\ =\sum _{n=0}^{\infty }x^{n}P_{n}(cos(b))\ .}$ If we let ${\displaystyle x={\frac {r1}{R}}}$ then we get the result,

${\displaystyle {\frac {1}{r}}={\frac {1}{R}}\sum _{n=0}^{\infty }\left({\frac {r1}{R}}\right)^{n}P_{n}(cos(b))\ .}$

Consider the function,

${\displaystyle f({\frac {x}{R}})=\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {1}{2}}}\ .}$

${\displaystyle f'({\frac {x}{R}})=\left(cos(\beta )-\left({\frac {x}{R}}\right)\right)\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {3}{2}}}}$

${\displaystyle f''({\frac {x}{R}})=-\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {3}{2}}}}$ ${\displaystyle +3\left(cos(\beta )-\left({\frac {x}{R}}\right)\right)^{2}\left(1-2cos(\beta )\left({\frac {x}{R}}\right)+\left({\frac {x}{R}}\right)^{2}\right)^{-{\frac {5}{2}}}\ .}$

GPS pictures

I've improved the diagramm for the GPS articles, as replacement for the raster picture. You removed the picture because there was no bus (from change description). Is the picture OK now ? Does it needs some correction ? Other pictures (I've made) have also been removed (for other reasons). I tried to make better picture (vector drawings), but with errors apparently. Could you also please contact the author of the picture to correct them , rather then just removing them. Thanks --Tsaitgaist (talk) 11:39, 10 February 2010 (UTC)

I've also update this picture as replacement for this picture. The polar axis are now vertical.--Tsaitgaist (talk) 13:58, 10 February 2010 (UTC)

Now this picture looks more like this one. --Tsaitgaist (talk) 14:09, 10 February 2010 (UTC)

However, I still disagree with you regarding, File:Gps error diagram.svg. This drawing looks more like a flow chart than a geometric figure and gives the false impression that the errors are all in the same direction and thus additive in my opinion. RHB100 (talk) 21:10, 10 February 2010 (UTC)

I'm happy to correct it, but I don't understand the error. Should it be horizontal rather then vertical ? Should the bubbles go up ? Are there missing or too many arrows ? I read the 2 diagrams the same way, but I'm just a drawer, there might be a technical aspect I don't see.--Tsaitgaist (talk) 14:24, 12 February 2010 (UTC)

Why don't you go ahead and add the figure, File:Lat 2spheres 2.svg, since we both agree that this is a good figure, the color serves to distinguish the 2 spheres and the readers may appreciate a little color in the figures. After that we can discuss the figure on which we disagree. RHB100 (talk) 22:22, 12 February 2010 (UTC) RHB100 (talk) 22:25, 12 February 2010 (UTC)

I was just too lazy :p. I waited for all the drawings to be ok to change them. I've change the correct ones. We can discuss to correct and enhance the last picture to fit the article --Tsaitgaist (talk) 10:21, 13 February 2010 (UTC)

Why don't you go ahead and add the figure, File:Lat 2spheres 2.svg, since we both agree that this is a good figure, the color serves to distinguish the 2 spheres and the readers may appreciate a little color in the figures. After that we can discuss the figure on which we disagree. RHB100 (talk) 22:22, 12 February 2010 (UTC)

I was just too lazy :p. I waited for all the drawings to be ok to change them. Now it's done. We can discuss to correct and enhance the picture to fit the article --Tsaitgaist (talk) 10:21, 13 February 2010 (UTC)

I don't think there is anything wrong with File:Gps error diagram.jpg. I think it shluld bel left as it is. Can you find anything wrong with it and if so what? RHB100 (talk) 19:49, 15 February 2010 (UTC)

The current picture is just of poor quality (the picture as file, not the information it contains). The size of the canvas it too big for the diagram (a lot of blank space), you can also see compression artifacts around all the diagram. A vector graphic file has also more benefits : it's scalable (if you zoom you don't loose quality, the diagram quality remains), it's easily modifiable by others (change the position/color/... of the objects), it's easy to translate (for wikis in other languages). There is no drawback. SVG is a lot more adapted for diagrams. I'm just vectorizing the pictures I see in the articles I read to enhance the quality of them. --Tsaitgaist (talk) 21:58, 16 February 2010 (UTC)

I created the diagram to make the effect of errors more understandable. I can increase from the thumbnail to full size with no noticeable loss of quality. I am not sure you fully understand the reason why it is drawn as it is. Therefore if you want to draw it as a .svg file, it is necessary that you draw just as it is. RHB100 (talk) 22:52, 16 February 2010 (UTC)

Now it's like the original. I do not understand everything in the diagram. Here the aspects it don't understand :

1. why do the bubbles go up
2. is it important that it goes from left to right (the arrow already indicates the direction)
3. why is the arrow between the two first bubbles longer then the two last. Is this error more important
4. why does "numerical error" have an arrow and not "effect of incorrect pseudo range ..."

Because I thought these were not important details, I erased them in the first pictures, so to not have the other readers ask the same questions and get confused. --Tsaitgaist (talk) 10:21, 17 February 2010 (UTC)

I think you have made valuable contributions to the GPS article with the figures you have already added. However, I ask that you leave the error diagram. File:Gps error diagram.jpg, as it is. I think the time spent for you to continue asking questions and for me to try to answer then is not worth it. I am sure that you have the talents to make improvements in many other areas. In summary you have made valuable contributions with improvement of GPS figures. But let's just leave the error diagram as it is. RHB100 (talk) 20:45, 17 February 2010 (UTC)

Wikiquette alert

Hello, RHB100. This message is being sent to inform you that there currently is a discussion at Misplaced Pages:Wikiquette alerts regarding an issue with which you may have been involved. Thank you. Ozob (talk) 05:54, 13 March 2010 (UTC)

Bad writing of Sławomir Biały 1: A vector does not designate a point

There are many things wrong with the writing of Biały. One place we can start is by pointing out that a vector does not designate a point. Biały makes the mistake of referring to the point, x, where x is a vector.

A vector has only a direction and a magnitude. It does not have a location. A vector beginning at the point (x,y,z) = (0,0,0) and ending at the point, (x,y,z) = (2,0,0), is exactly the same as a vector beginning at the point (x,y,z) = (5,0,0) and ending at the point, (x,y,z) = (7,0,0). This is true since they both have the same magnitude and direction.

Thus a vector certainly does not designate a point and the writing of Biały shows a failure to understand very basic fundamentals on the nature of vectors and points. RHB100 (talk) 21:53, 13 March 2010 (UTC)

ANI notice

Hello. This message is being sent to inform you that there currently is a discussion at Misplaced Pages:Administrators' noticeboard/Incidents regarding an issue with which you may have been involved. Thank you. Ozob (talk) 23:31, 13 March 2010 (UTC)

1. Water, Water by Neil deGrasse Tyson
2. Lide, D. R., ed. (2005). CRC Handbook of Chemistry and Physics (86th ed.). Boca Raton, Florida: CRC Press. ISBN 0-8493-0486-5.