This is an old revision of this page, as edited by Chbarts (talk | contribs) at 05:23, 1 February 2011 (→History: removed uncited, untrue statement). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 05:23, 1 February 2011 by Chbarts (talk | contribs) (→History: removed uncited, untrue statement)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)The first IEEE Standard for Binary Floating-Point Arithmetic (IEEE 754-1985) set the standard for floating-point computation for 23 years. It became the most widely-used standard for floating-point computation, and is followed by many CPU and FPU implementations. Its binary floating-point formats and arithmetic are preserved in the new IEEE 754-2008 standard which replaced it.
The 754-1985 standard defines formats for representing floating-point numbers (including negative zero and denormal numbers) and special values (infinities and NaNs) together with a set of floating-point operations that operate on these values. It also specifies four rounding modes and five exceptions (including when the exceptions occur, and what happens when they do occur).
Summary
IEEE 754-1985 specifies four formats for representing floating-point values: single-precision (32-bit), double-precision (64-bit), single-extended precision (≥ 43-bit, not commonly used) and double-extended precision (≥ 79-bit, usually implemented with 80 bits). Only 32-bit values are required by the standard; the others are optional. Many languages specify that IEEE formats and arithmetic be implemented, although sometimes it is optional. For example, the C programming language, which pre-dated IEEE 754, now allows but does not require IEEE arithmetic (the C float typically is used for IEEE single-precision and double uses IEEE double-precision).
The full title of the standard is IEEE Standard for Binary Floating-Point Arithmetic (ANSI/IEEE Std 754-1985), and it is also known as IEC 60559:1989, Binary floating-point arithmetic for microprocessor systems (originally the reference number was IEC 559:1989). Later there was an IEEE 854-1987 for "radix independent floating point" as long as the radix is 2 or 10. In June 2008, a major revision to IEEE 754 and IEEE 854 was approved by the IEEE. See IEEE 754r.
Structure of a floating-point number
General layout

Binary floating-point numbers in IEEE 754-1985 format consist of three fields: sign bit, exponent, and fraction. The fraction is the significand without its most significant bit.
Exponent biasing
Instead of being stored in two's complement format, the exponent is stored in "biased format" (offset binary): a constant, called the bias, is added to it so that the lowest representable exponent is represented as 1, and there is no sign bit. The bias is equal to 2−1, where n is the number of bits in the exponent field. Thus the actual number stored in the exponent field is the true exponent plus the bias.
For example, in single-precision format, where the exponent field is 8 bits long, the bias is 2−1 = 128 − 1 = 127. So, for example, an exponent of 17 would be represented as 144 in single precision (144 = 17 + 127).
Cases
The most significant bit of the significand (not stored) is determined by the value of biased exponent. If exponent , the most significant bit of the significand is 1, and the number is said to be normalized. If exponent is 0 and fraction is not 0, the most significant bit of the significand is 0 and the number is said to be de-normalized. Three other special cases arise:
- if exponent is 0 and fraction is 0, the number is ±0 (depending on the sign bit)
- if exponent = and fraction is 0, the number is ±infinity (again depending on the sign bit), and
- if exponent = and fraction is not 0, the number being represented is not a number (NaN).
This can be summarized as:
| Type | Exponent | Fraction |
|---|---|---|
| Zeroes | 0 | 0 |
| Denormalized numbers | 0 | non zero |
| Normalized numbers | to | any |
| Infinities | 0 | |
| NaNs | non zero |
Single-precision 32-bit
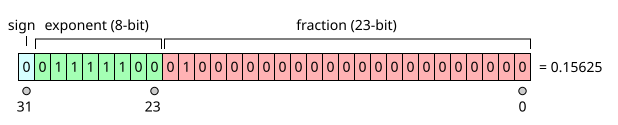
A single-precision binary floating-point number is stored in 32 bits, as shown at right.
If the number is normalized (the most common case), it has this value:
where:
- sign = the sign bit. (0 makes the number positive or zero; 1 makes it negative.)
- expo = the 8-bit number stored in the exponent field. expo = the true exponent + 127. (See above for why.)
- fraction = the 23 bits of the fraction field.
In the example, the sign is 0, so the number is positive; expo is 124, so the true exponent is –3; and fraction is .01. So, the represented number is:
(Subscripts indicate the base of the number: base 2 or base 10.)
Notes
- Denormalized numbers are the same except that e = −126 and m is 0.fraction. (e is not −127 : The fraction has to be shifted to the right by one more bit, in order to include the leading bit, which is not always 1 in this case. This is balanced by incrementing the exponent to −126 for the calculation.)
- −126 is the smallest exponent for a normalized number
- There are two Zeroes, +0 (s is 0) and −0 (s is 1)
- There are two Infinities +∞ (s is 0) and −∞ (s is 1)
- NaNs may have a sign and a fraction, but these have no meaning other than for diagnostics; the first bit of the fraction is often used to distinguish signaling NaNs from quiet NaNs
- NaNs and Infinities have all 1s in the Exp field.
- The positive and negative numbers closest to zero (represented by the denormalized value with all 0s in the Exp field and the binary value 1 in the Fraction field) are
- ±2 ≈ ±1.4012985×10
- The positive and negative normalized numbers closest to zero (represented with the binary value 1 in the Exp field and 0 in the fraction field) are
- ±2 ≈ ±1.175494351×10
- The finite positive and finite negative numbers furthest from zero (represented by the value with 254 in the Exp field and all 1s in the fraction field) are
- ±(1-2)×2 ≈ ±3.4028235×10
Here is the summary table from the previous section with some 32-bit single-precision examples:
| Type | Sign | Exp | Exp+Bias | Exponent | Significand (Mantissa) | Value |
|---|---|---|---|---|---|---|
| Zero | 0 | -127 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | 0.0 |
| Negative zero | 1 | -127 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0000 | −0.0 |
| One | 0 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | 1.0 |
| Minus One | 1 | 0 | 127 | 0111 1111 | 000 0000 0000 0000 0000 0000 | −1.0 |
| Smallest denormalized number | * | -127 | 0 | 0000 0000 | 000 0000 0000 0000 0000 0001 | ±2 × 2 = ±2 ≈ ±1.4×10 |
| "Middle" denormalized number | * | -127 | 0 | 0000 0000 | 100 0000 0000 0000 0000 0000 | ±2 × 2 = ±2 ≈ ±5.88×10 |
| Largest denormalized number | * | -127 | 0 | 0000 0000 | 111 1111 1111 1111 1111 1111 | ±(1−2) × 2 ≈ ±1.18×10 |
| Smallest normalized number | * | -126 | 1 | 0000 0001 | 000 0000 0000 0000 0000 0000 | ±2 ≈ ±1.18×10 |
| Largest normalized number | * | 127 | 254 | 1111 1110 | 111 1111 1111 1111 1111 1111 | ±(2−2) × 2 ≈ ±3.4×10 |
| Positive infinity | 0 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | +∞ |
| Negative infinity | 1 | 128 | 255 | 1111 1111 | 000 0000 0000 0000 0000 0000 | −∞ |
| Not a number | * | 128 | 255 | 1111 1111 | non zero | NaN |
| * Sign bit can be either 0 or 1 . | ||||||
Range and Precision Table
Precision is defined as the min. difference between two successive mantissa representations; thus it is function only in the mantissa; while the gap is defined as the difference between two successive numbers..
Some example range and gap values for given exponents:
| Exponent | Minimum | Maximum | Gap |
|---|---|---|---|
| 0 | 1 | 1.999999880791 | 1.19209289551e-7 |
| 1 | 2 | 3.99999976158 | 2.38418579102e-7 |
| 2 | 4 | 7.99999952316 | 4.76837158203e-7 |
| 10 | 1024 | 2047.99987793 | 1.220703125e-4 |
| 11 | 2048 | 4095.99975586 | 2.44140625e-4 |
| 23 | 8388608 | 16777215 | 1 |
| 24 | 16777216 | 33554430 | 2 |
| 127 | 1.7014e38 | 3.4028e38 | 2.02824096037e31 |
As an example, 16,777,217 can not be encoded as a 32-bit float as it will be rounded to 16,777,216. This shows why floating point arithmetic is unsuitable for accounting software. However, all integers within the representable range that are a power of 2 can be stored in a 32-bit float without rounding.
A more complex example

The decimal number −118.625 is encoded using the IEEE 754 system as follows:
- The sign, the exponent, and the fraction are extracted from the original number. Because the number is negative, the sign bit is "1".
- Next, the number (without the sign; i.e., unsigned, no two's complement) is converted to binary notation, giving 1110110.101. The 101 after the binary point has the value 0.625 because it is the sum of:
- (2) × 1, from the first bit after the binary point
- (2) × 0, from the second bit
- (2) × 1, from the third bit.
- That binary number is then normalized; that is, the binary point is moved left, leaving only a 1 to its left. The number of places it is moved gives the (power of two) exponent: 1110110.101 becomes 1.110110101 × 2. After this process, the first binary digit is always a 1, so it need not be included in the encoding. The rest is the part to the right of the binary point, which is then padded with zeros on the right to make 23 bits in all, which becomes the significand bits in the encoding: That is, 11011010100000000000000.
- The exponent is 6. This is encoded by converting it to binary and biasing it (so the most negative encodable exponent is 0, and all exponents are non-negative binary numbers). For the 32-bit IEEE 754 format, the bias is +127 and so 6 + 127 = 133. In binary, this is encoded as 10000101.
Double-precision 64 bit
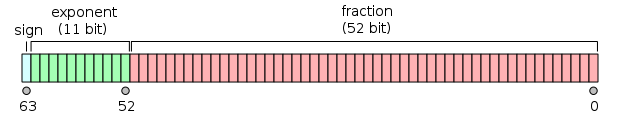
Double precision is essentially the same except that the fields are wider:
The fraction part is much larger, while the exponent is only slightly larger. NaNs and Infinities are represented with Exp being all 1s (2047). If the fraction part is all zero then it is Infinity, else it is NaN.
For Normalized numbers the exponent bias is +1023 (so e is exponent − 1023). For Denormalized numbers the exponent is (−1022) (the minimum exponent for a normalized number—it is not (−1023) because normalised numbers have a leading 1 digit before the binary point and denormalized numbers do not). As before, both infinity and zero are signed.
Notes:
- The positive and negative numbers closest to zero (represented by the denormalized value with all 0s in the Exp field and the binary value 1 in the Fraction field) are
- ±2 ≈ ±5×10
- The positive and negative normalized numbers closest to zero (represented with the binary value 1 in the Exp field and 0 in the fraction field) are
- ±2 ≈ ±2.2250738585072020×10
- The finite positive and finite negative numbers furthest from zero (represented by the value with 2046 in the Exp field and all 1s in the fraction field) are
- ±((1-(1/2))2) ≈ ±1.7976931348623157×10
Some example range and gap values for given exponents:
| Exponent | Minimum | Maximum | Gap |
|---|---|---|---|
| 0 | 1 | 1.9999999999999997 | 2.2204460492503130808472633e-16 |
| 1 | 2 | 3.9999999999999995 | 8.8817841970012523233890533447266e-16 |
| 2 | 4 | 7.9999999999999990 | 3.5527136788005009293556213378906e-15 |
| 10 | 1024 | 2047.9999999999997 | 2.27373675443232059478759765625e-13 |
| 11 | 2048 | 4095.9999999999995 | 4.5474735088646411895751953125e-13 |
| 52 | 4503599627370496 | 9007199254740991 | 1 |
| 53 | 9007199254740992 | 18014398509481982 | 2 |
| 1023 | 8.9884656743115800e+307 | 1.7976931348623157e308 | 1.9958403095347198116563727130368e292 |
Comparing floating-point numbers
Every possible bit combination is either a NaN or a number with a unique value in the affinely extended real number system with its associated order, except for the two bit combinations negative zero and positive zero, which sometimes require special attention (see below). The binary representation has the special property that, excluding NaNs, any two numbers can be compared like sign and magnitude integers (although with modern computer processors this is no longer directly applicable): if the sign bit is different, the negative number precedes the positive number (except that negative zero and positive zero should be considered equal), otherwise, relative order is the same as lexicographical order but inverted for two negative numbers; endianness issues apply.
Floating-point arithmetic is subject to rounding that may affect the outcome of comparisons on the results of the computations.
Although negative zero and positive zero are generally considered equal for comparison purposes, some programming language relational operators and similar constructs might or do treat them as distinct. According to the Java Language Specification, comparison and equality operators treat them as equal, but Math.min() and Math.max() distinguish them (officially starting with Java version 1.1 but actually with 1.1.1), as do the comparison methods equals(), compareTo() and even compare() of classes Float and Double.
Rounding floating-point numbers
The IEEE standard has four different rounding modes; the first is the default; the others are called directed roundings.
- Round to Nearest – rounds to the nearest value; if the number falls midway it is rounded to the nearest value with an even (zero) least significant bit, which occurs 50% of the time (in IEEE 754r this mode is called roundTiesToEven to distinguish it from another round-to-nearest mode)
- Round toward 0 – directed rounding towards zero
- Round toward – directed rounding towards positive infinity
- Round toward – directed rounding towards negative infinity.
Extending the real numbers
The IEEE standard employs (and extends) the affinely extended real number system, with separate positive and negative infinities. During drafting, there was a proposal for the standard to incorporate the projectively extended real number system, with a single unsigned infinity, by providing programmers with a mode selection option. In the interest of reducing the complexity of the final standard, the projective mode was dropped, however. The Intel 8087 and Intel 80287 floating point co-processors both support this projective mode.
Functions and predicates
Standard operations
The following functions must be provided:
- Add, subtract, multiply, divide
- Square root
- Floating point remainder. This is not like a normal modulo operation, it can be negative for two positive numbers. It returns the exact value of x-(round(x/y)*y).
- Round to nearest integer. For undirected rounding when halfway between two integers the even integer is chosen.
- Comparison operations. Besides the more obvious results, IEEE754 defines that -inf = -inf, inf = inf and x ≠ NaN for any x (including NaN).
Recommended functions and predicates
- Under some C compilers,
copysign(x,y)returns x with the sign of y, soabs(x)equalscopysign(x,1.0). This is one of the few operations which operates on a NaN in a way resembling arithmetic. The functioncopysignis new in the C99 standard. - −x returns x with the sign reversed. This is different from 0−x in some cases, notably when x is 0. So −(0) is −0, but the sign of 0−0 depends on the rounding mode.
scalb(y, N)logb(x)finite(x)a predicate for "x is a finite value", equivalent to −Inf < x < Infisnan(x)a predicate for "x is a nan", equivalent to "x ≠ x"x <> ywhich turns out to have different exception behavior than NOT(x = y).unordered(x, y)is true when "x is unordered with y", i.e., either x or y is a NaN.class(x)nextafter(x,y)returns the next representable value from x in the direction towards y
History
In 1976 Intel began planning to produce a floating point coprocessor. Dr John Palmer, the manager of the effort, persuaded them that they should try to develop a standard for all their floating point operations. William Kahan was hired as a consultant; he had helped improve the accuracy of Hewlett Packard's calculators. Kahan initially recommended that the floating point base be decimal but the hardware design of the coprocessor was too far advanced to make that change.
The work within Intel worried other vendors, who set up a standardization effort to ensure a 'level playing field'. Kahan attended the second IEEE 754 standards working group meeting, held in November 1977. Here, he received permission from Intel to put forward a draft proposal based on the standard arithmetic part of their design for a coprocessor. The formats were similar to but slightly different from existing VAX and CDC formats and introduced gradual underflow. The arguments over gradual underflow lasted until 1981 when an expert commissioned by DEC to assess it sided against the dissenters.
Even before it was approved, the draft standard had been implemented by a number of manufacturers.
The Zuse Z3 implemented floating point with infinities and undefined values which were passed through operations. These were not implemented properly in hardware in any other machine until the Intel 8087, which was announced in 1980. This was the first chip to implement the draft standard.
See also
- IEEE 754-2008
- −0 (negative zero)
- Intel 8087
- minifloat for simple examples of properties of IEEE 754 floating point numbers
- Q (number format) For constant resolution
References
- "Referenced documents".
IEC 60559:1989, Binary Floating-Point Arithmetic for Microprocessor Systems (previously designated IEC 559:1989)
- ^ Prof. W. Kahan. "Lecture Notes on the Status of IEEE 754" (PDF). October 1, 1997 3:36 am. Elect. Eng. & Computer Science University of California. Retrieved 2007-04-12.
{{cite journal}}: Cite journal requires|journal=(help) - Computer Arithmetic; Hossam A. H. Fahmy, Shlomo Waser, and Michael J. Flynn; http://arith.stanford.edu/~hfahmy/webpages/arith_class/arith.pdf
- The Java Language Specification
- John R. Hauser (1996). "Handling Floating-Point Exceptions in Numeric Programs" (PDF). ACM Transactions on Programming Languages and Systems. 18 (2).
{{cite journal}}: Unknown parameter|month=ignored (help) - David Stevenson (1981). "IEEE Task P754: A proposed standard for binary floating-point arithmetic". IEEE Computer. 14 (3): 51–62.
{{cite journal}}: Unknown parameter|month=ignored (help) - William Kahan and John Palmer (1979). "On a proposed floating-point standard". SIGNUM Newsletter. 14 (Special): 13–21. doi:10.1145/1057520.1057522.
- W. Kahan 2003, pers. comm. to Mike Cowlishaw and others after an IEEE 754 meeting
- Charles Severance (20 February 1998). "An Interview with the Old Man of Floating-Point".
- Charles Severance. "History of IEEE Floating-Point Format". Connexions.
Further reading
- Charles Severance (1998). "IEEE 754: An Interview with William Kahan" (PDF). IEEE Computer. 31 (3): 114–115. doi:10.1109/MC.1998.660194. Retrieved 2008-04-28.
{{cite journal}}: Unknown parameter|month=ignored (help) - David Goldberg (1991). "What Every Computer Scientist Should Know About Floating-Point Arithmetic" (PDF). ACM Computing Surveys. 23 (1): 5–48. doi:10.1145/103162.103163. Retrieved 2008-04-28.
{{cite journal}}: Unknown parameter|month=ignored (help) - Chris Hecker (1996). "Let's Get To The (Floating) Point" (PDF). Game Developer Magazine: 19–24. ISSN 1073-922X.
{{cite journal}}: Unknown parameter|month=ignored (help) - David Monniaux (2008). "The pitfalls of verifying floating-point computations". ACM Transactions on Programming Languages and Systems. 30 (3): article #12. doi:10.1145/1353445.1353446. ISSN 0164-0925.
{{cite journal}}: Unknown parameter|month=ignored (help): A compendium of non-intuitive behaviours of floating-point on popular architectures, with implications for program verification and testing.
External links
- Comparing floats
- Coprocessor.info: x87 FPU pictures, development and manufacturer information
- IEEE 754 references
- IEEE 854-1987 — History and minutes
- Online IEEE 754 Calculators
- IEEE754 (Single and Double precision) Online Converter
| IEEE standards | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Current | |||||||||||
| 802 series |
| ||||||||||
| Proposed | |||||||||||
| Superseded | |||||||||||
 exponent
exponent  , the most significant bit of the significand is 1, and the number is said to be normalized. If exponent is 0 and fraction is not 0, the most significant bit of the significand is 0 and the number is said to be de-normalized. Three other special cases arise:
, the most significant bit of the significand is 1, and the number is said to be normalized. If exponent is 0 and fraction is not 0, the most significant bit of the significand is 0 and the number is said to be de-normalized. Three other special cases arise:
 and fraction is 0, the number is ±
and fraction is 0, the number is ± to
to 


 – directed rounding towards positive infinity
– directed rounding towards positive infinity – directed rounding towards negative infinity.
– directed rounding towards negative infinity.