


The Chialvo map is a two-dimensional map proposed by Dante R. Chialvo in 1995 to describe the generic dynamics of excitable systems. The model is inspired by Kunihiko Kaneko's Coupled map lattice numerical approach which considers time and space as discrete variables but state as a continuous one. Later on Rulkov popularized a similar approach. By using only three parameters the model is able to efficiently mimic generic neuronal dynamics in computational simulations, as single elements or as parts of inter-connected networks.
The model
The model is an iterative map where at each time step, the behavior of one neuron is updated as the following equations:
in which, is called activation or action potential variable, and is the recovery variable. The model has four parameters, is a time-dependent additive perturbation or a constant bias, is the time constant of recovery , is the activation-dependence of the recovery process and is an offset constant. The model has a rich dynamics, presenting from oscillatory to chaotic behavior, as well as non trivial responses to small stochastic fluctuations.
Analysis
Bursting and chaos
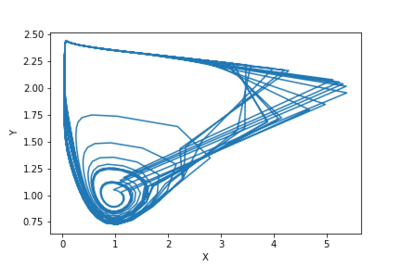
The map is able to capture the aperiodic solutions and the bursting behavior which are remarkable in the context of neural systems. For example, for the values , and and changing b from to the system passes from oscillations to aperiodic bursting solutions.
Fixed points
Considering the case where and the model mimics the lack of ‘voltage-dependence inactivation’ for real neurons and the evolution of the recovery variable is fixed at . Therefore, the dynamics of the activation variable is basically described by the iteration of the following equations
in which as a function of has a period-doubling bifurcation structure.
Examples
Example 1
A practical implementation is the combination of neurons over a lattice, for that, it can be defined as a coupling constant for combining the neurons. For neurons in a single row, we can define the evolution of action potential on time by the diffusion of the local temperature in:
where is the time step and is the index of each neuron. For the values , , and , in absence of perturbations they are at the resting state. If we introduce a stimulus over cell 1, it induces two propagated waves circulating in opposite directions that eventually collapse and die in the middle of the ring.
Example 2
Analogous to the previous example, it's possible create a set of coupling neurons over a 2-D lattice, in this case the evolution of action potentials is given by:
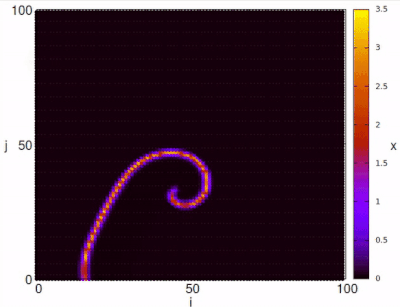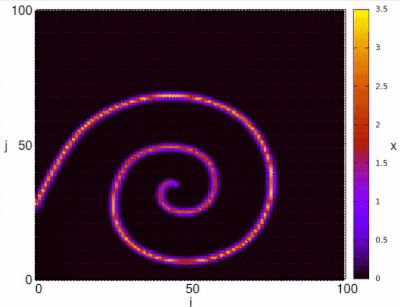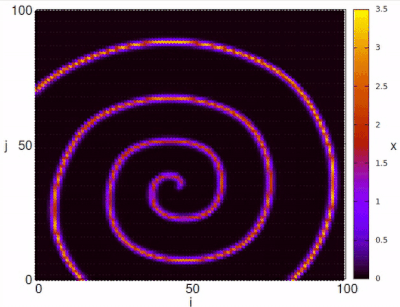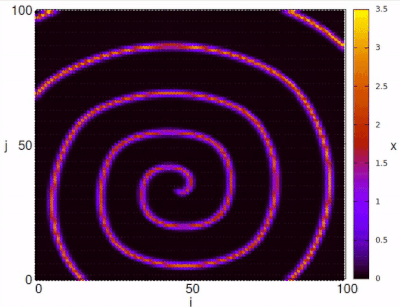
where , , represent the index of each neuron in a square lattice of size , . With this example spiral waves can be represented for specific values of parameters. In order to visualize the spirals, we set the initial condition in a specific configuration and the recovery as .
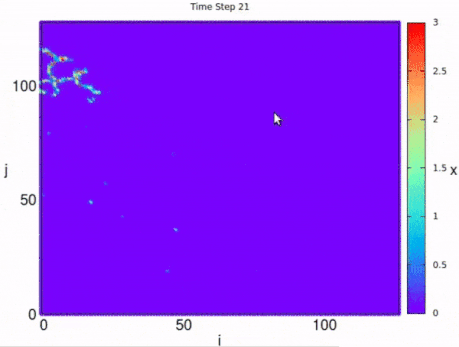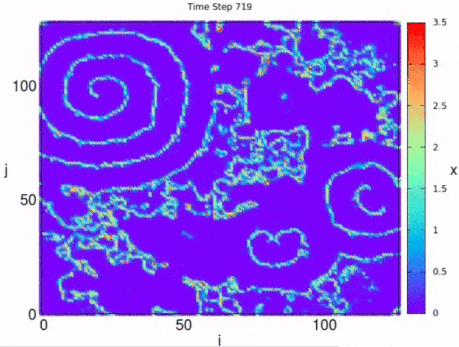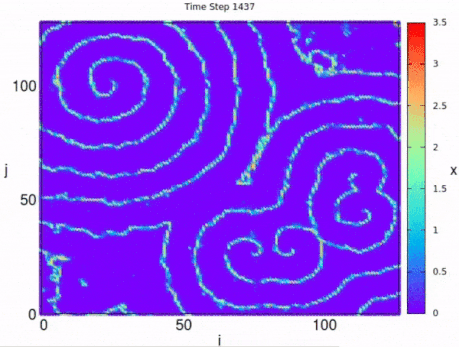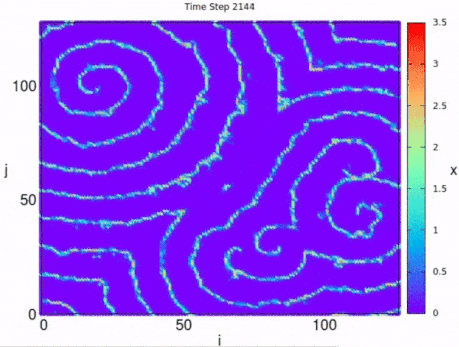
The map can also present chaotic dynamics for certain parameter values. In the following figure we show the chaotic behavior of the variable on a square network of for the parameters , , and .

The map can be used to simulated a nonquenched disordered lattice (as in Ref ), where each map connects with four nearest neighbors on a square lattice, and in addition each map has a probability of connecting to another one randomly chosen, multiple coexisting circular excitation waves will emerge at the beginning of the simulation until spirals takes over.
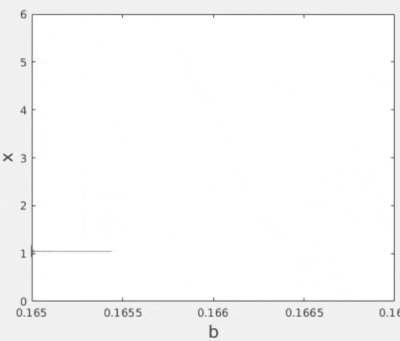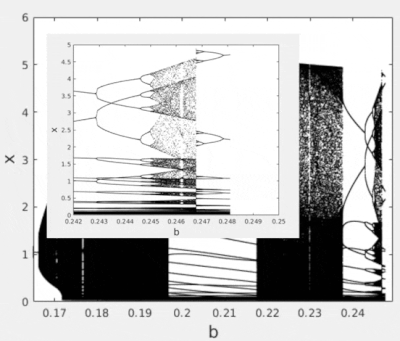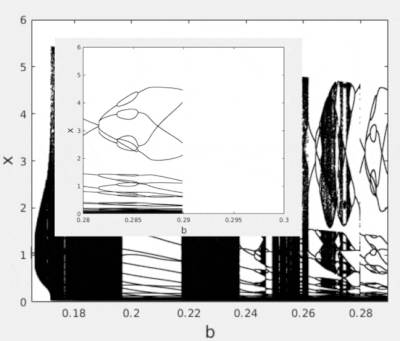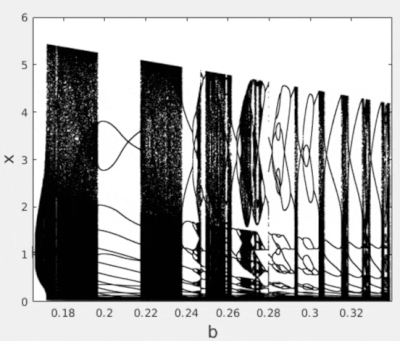
Chaotic and periodic behavior for a neuron
For a neuron, in the limit of , the map becomes 1D, since converges to a constant. If the parameter is scanned in a range, different orbits will be seen, some periodic, others chaotic, that appear between two fixed points, one at ; and the other close to the value of (which would be the regime excitable).

References
- Chialvo, Dante R. (1995-03-01). "Generic excitable dynamics on a two-dimensional map". Chaos, Solitons & Fractals. Nonlinear Phenomena in Excitable Physiological Systems. 5 (3): 461–479. Bibcode:1995CSF.....5..461C. doi:10.1016/0960-0779(93)E0056-H. ISSN 0960-0779.
- Rulkov, Nikolai F. (2002-04-10). "Modeling of spiking-bursting neural behavior using two-dimensional map". Physical Review E. 65 (4): 041922. arXiv:nlin/0201006. Bibcode:2002PhRvE..65d1922R. doi:10.1103/PhysRevE.65.041922. PMID 12005888. S2CID 1998912.
- Pilarczyk, Paweł; Signerska-Rynkowska, Justyna; Graff, Grzegorz (2022-09-07). "Topological-numerical analysis of a two-dimensional discrete neuron model". arXiv:2209.03443 .
- Wang, Fengjuan; Cao, Hongjun (2018-03-01). "Mode locking and quasiperiodicity in a discrete-time Chialvo neuron model". Communications in Nonlinear Science and Numerical Simulation. 56: 481–489. Bibcode:2018CNSNS..56..481W. doi:10.1016/j.cnsns.2017.08.027. ISSN 1007-5704.
- Chialvo, Dante R.; Apkarian, A. Vania (1993-01-01). "Modulated noisy biological dynamics: Three examples". Journal of Statistical Physics. 70 (1): 375–391. Bibcode:1993JSP....70..375C. doi:10.1007/BF01053974. ISSN 1572-9613. S2CID 121830779.
- Bashkirtseva, Irina; Ryashko, Lev; Used, Javier; Seoane, Jesús M.; Sanjuán, Miguel A. F. (2023-01-01). "Noise-induced complex dynamics and synchronization in the map-based Chialvo neuron model". Communications in Nonlinear Science and Numerical Simulation. 116: 106867. Bibcode:2023CNSNS.11606867B. doi:10.1016/j.cnsns.2022.106867. ISSN 1007-5704. S2CID 252140483.
- Sinha, Sitabhra; Saramäki, Jari; Kaski, Kimmo (2007-07-09). "Emergence of self-sustained patterns in small-world excitable media". Physical Review E. 76 (1): 015101. arXiv:cond-mat/0701121. Bibcode:2007PhRvE..76a5101S. doi:10.1103/PhysRevE.76.015101. ISSN 1539-3755. PMID 17677522. S2CID 11714109.

 is called activation or action potential variable, and
is called activation or action potential variable, and  is the recovery variable. The model has four parameters,
is the recovery variable. The model has four parameters,  is a time-dependent additive perturbation or a constant bias,
is a time-dependent additive perturbation or a constant bias,  is the time constant of recovery
is the time constant of recovery  ,
,  is the activation-dependence of the recovery process
is the activation-dependence of the recovery process  and
and  is an offset constant. The model has a rich dynamics, presenting from oscillatory to chaotic behavior, as well as non trivial responses to small stochastic fluctuations.
is an offset constant. The model has a rich dynamics, presenting from oscillatory to chaotic behavior, as well as non trivial responses to small stochastic fluctuations.
 ,
,  and
and  and changing b from
and changing b from  to
to  the system passes from oscillations to aperiodic bursting solutions.
the system passes from oscillations to aperiodic bursting solutions.
 and
and  the model mimics the lack of ‘voltage-dependence inactivation’ for real neurons and the evolution of the recovery variable is fixed at
the model mimics the lack of ‘voltage-dependence inactivation’ for real neurons and the evolution of the recovery variable is fixed at  . Therefore, the dynamics of the activation variable is basically described by the iteration of the following equations
. Therefore, the dynamics of the activation variable is basically described by the iteration of the following equations

 as a function of
as a function of  has a period-doubling bifurcation structure.
has a period-doubling bifurcation structure.
 neurons over a lattice, for that, it can be defined
neurons over a lattice, for that, it can be defined  as a coupling constant for combining the neurons. For neurons in a single row, we can define the evolution of action potential on time by the diffusion of the local temperature
as a coupling constant for combining the neurons. For neurons in a single row, we can define the evolution of action potential on time by the diffusion of the local temperature 
 is the time step and
is the time step and  is the index of each neuron. For the values
is the index of each neuron. For the values  ,
,  , in absence of perturbations they are at the resting state. If we introduce a stimulus over cell 1, it induces two propagated waves circulating in opposite directions that eventually collapse and die in the middle of the ring.
, in absence of perturbations they are at the resting state. If we introduce a stimulus over cell 1, it induces two propagated waves circulating in opposite directions that eventually collapse and die in the middle of the ring.

 , represent the index of each neuron in a square lattice of size
, represent the index of each neuron in a square lattice of size  ,
,  . With this example spiral waves can be represented for specific values of parameters. In order to visualize the spirals, we set the initial condition in a specific configuration
. With this example spiral waves can be represented for specific values of parameters. In order to visualize the spirals, we set the initial condition in a specific configuration  and the recovery as
and the recovery as  .
.
 for the parameters
for the parameters  ,
,  .
.
 of connecting to another one randomly chosen, multiple coexisting circular excitation waves will emerge at the beginning of the simulation until spirals takes over.
of connecting to another one randomly chosen, multiple coexisting circular excitation waves will emerge at the beginning of the simulation until spirals takes over.
 and parameters a=0.89, b=0.6, c= 0.26, and k=0.02.
and parameters a=0.89, b=0.6, c= 0.26, and k=0.02. , the map becomes 1D, since
, the map becomes 1D, since  ;
;  and the other close to the value of
and the other close to the value of  to
to  .
.