| This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (December 2016) |
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Coxeter decompositions of hyperbolic polygons" – news · newspapers · books · scholar · JSTOR (June 2017) (Learn how and when to remove this message) |

A Coxeter decomposition of a polygon is a decomposition into a finite number of polygons in which any two sharing a side are reflections of each other along that side. Hyperbolic polygons are the analogues of Euclidean polygons in hyperbolic geometry. A hyperbolic n-gon is an area bounded by n segments, rays, or entire straight lines. The standard model for this geometry is the Poincaré disk model. A major difference between Euclidean and hyperbolic polygons is that the sum of internal angles of a hyperbolic polygon is not the same as Euclidean polygons. In particular, the sum of the angles of a hyperbolic triangle is less than 180 degrees.
Coxeter decompositions are named after Harold Scott MacDonald Coxeter, an accomplished 20th century geometer. He introduced the Coxeter group, an abstract group generated by reflections. These groups have many uses, including producing the rotations of Platonic solids and tessellating the plane.
Coxeter decompositions
Given a polygon P, a group G can be generated by reflecting P around its sides. If the angles of P are π/k for natural numbers k, then G will be discrete. A Coxeter decomposition of a polygon is a decomposition into a finite number of polygons in which any two sharing a side are reflections of each other along that side.
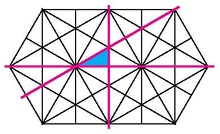
The goal of a Coxeter decomposition is to break up a polygon into a composition of congruent triangles reflected on its sides.
Hyperbolic triangles
If triangle ABC can undergo Coxeter decomposition and has angles , where is the number of times the th angle is broken up, the triangle ABC can be written as . Several properties of these fundamental polygons are known for hyperbolic triangles.

- The fundamental triangle has a right angle. The proof of this involves two cases dependent on if the angles of the decomposed triangle are fundamental. If they are not, then it follows that since the process of decomposition is finite, eventually a fundamental triangle will be formed with a right angle. If they are, a proof by contradiction based on the area of the fundamental triangle proves that it will have a right angle.
- For a triangle , at least two are equal. This is also proved by contradiction based on the area of the fundamental polygon found using the Gauss–Bonnet theorem. We can say the area of the whole triangle is equal to the number of fundamental triangles times their area. This gives us . If we assume that , then the previous equality is broken for . Therefore, at least two angles are equal.
- Given a triangle where all three angles are fundamental, there is a single decomposition. A nontrivial proof of this can be found in.
- All possible decompositions are known.

These are all Coxeter decompositions of hyperbolic triangles, excluding the more detailed one above.
Other hyperbolic polygons
Quadrilaterals may also have Coxeter decompositions.
- If a quadrilateral in not convex, then there are two possible triangular decompositions. This is done by decomposing it into two triangles are then decomposing those. These two triangles are obtuse.
- A quadrilateral can be decomposed by quadrilaterals.
- All decompositions of convex quadrilaterals are also known. Showing them all is impractical in this article, but some are pictured here.

The decompositions for nonconvex quadrilaterals. 
Decompositions of quadrilaterals into quadrilaterals

References
- Felikson, A. A. (1998). "Coxeter Decompositions of Hyperbolic Polygons". European J. Combin. 19 (7): 801–817. doi:10.1006/eujc.1998.0238.
 , where
, where  is the number of times the
is the number of times the  th angle is broken up, the triangle ABC can be written as
th angle is broken up, the triangle ABC can be written as  . Several properties of these fundamental polygons are known for hyperbolic triangles.
. Several properties of these fundamental polygons are known for hyperbolic triangles.
 are equal. This is also proved by contradiction based on the area of the fundamental polygon found using the
are equal. This is also proved by contradiction based on the area of the fundamental polygon found using the  . If we assume that
. If we assume that  , then the previous equality is broken for
, then the previous equality is broken for  . Therefore, at least two angles are equal.
. Therefore, at least two angles are equal.