| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2013) (Learn how and when to remove this message) |
| Dom Bédos de Celles | |
|---|---|
| Born | 24 January 1709 Caux, Hérault |
| Died | 25 November 1779 Paris |
| Occupation | Benedictine monk |
François-Lamathe Dom Bédos de Celles de Salelles (24 January 1709 – 25 November 1779) was a Benedictine monk best known for being a master pipe organ builder.
Life and work
He was born in Caux, Hérault, near Béziers, France. He was elected to the French Academy of Sciences at Bordeaux and correspondent of the academy at Paris in 1758.
As a recognized organ-builder, he was called upon to carry out repairs and appraise and advise other organ-builders in many locations across France.
In 1760 he published La Gnomonique pratique ou l’Art de tracer les cadrans solaires under the patronage of the Jean-Paul Grandjean de Fouchy, Secretary of the Academy of Sciences and an authority in gnomonics and sundials.
In 1766–78 he published his treatise L'art du facteur d'orgues (The Art of the Organ-Builder), a part of the series Descriptions des Arts et Métiers. Dom Bédos's work, in four folio volumes, contains great historical detail about eighteenth-century organ building, and is still referred to by modern organ-builders.
He is buried in the former Abbey (now Basilica) of Saint-Denis.
Organ building in the mid 18th century
The 26 images below are taken from this work, kept in the St. Bernard's abbey library in Bornem.
Horizontal Sundial layout
The Dom Francois Bedos de Celles method (1790) otherwise known as the Waugh method (1973), enables a dial to be constructed on a narrower piece of paper or velum, than using Dürers (1525) method- though it is essentially the same for the hourlines 9 to 3. It relies on a theorem proved on 1682 by P. de la Hire.
- Starting at the bottom of the paper, a line is drawn across, and a vertical one up the centre. Where they cross is the point O.
- Choose the size of the dial, and draw a line across. Where it crosses the centre line is F
- Using the selected latitude. a line is drawn from O at this angle, this is a construction line.
- Using a square, a line is dropped from F through the construction line so they cross at right angles. That point E is important. To be precise it is the line FE that is important as it is length .
- Using compasses, or dividers the length FE is copied upwards in the centre line from F. The new point is called G and yes it is important- the construction lines and FE may now be erased.
- From G a series of lines, 15° apart are drawn, long enough so they cross the line through F. These mark the hour points 9, 10, 11, 12, 1, 2, 3 and represent the points .
- The centre of the dial is at the bottom, point O. The line drawn from each of these hour point to O will be the hour line on the finished dial.
- However, Dom Bédos de Celles had a unique way of marking up 7 and 8, and 4 and 5. Call the point where 3 crosses the line R, and a drop a line at right-angles to the base line. Call that point W. Use a construction line to join W and F. Waugh, in his book, calls the crossing points with the hours lines K, L, M.
- Using compasses or dividers, add two more points to this line N and P, so that the distances MN = ML, and MP = MK. The missing hour lines are drawn from O through N and through P. The construction lines are erased. The P. de la Hire theorem established that if a line is parallel to the 9 hourline, that is line WF then all the hourlines will be symmetrical around the hourline 6 hours later (i.e. 3).
-
 Setting out a dial for 52°N. The three initial lines.
Setting out a dial for 52°N. The three initial lines.
-
 Marking the latitude, laying out length , and copying to G on the vertical.
Marking the latitude, laying out length , and copying to G on the vertical.
-
 From G casting on the horizontal.
From G casting on the horizontal.
-
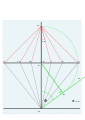 The actual hour lines 9, 10, 11, 12, 1, 2, 3.
The actual hour lines 9, 10, 11, 12, 1, 2, 3.
-
 Construction lines removed.
Construction lines removed.
-
 Constructing the 7, 8, 4, 5 lines
Constructing the 7, 8, 4, 5 lines
-
 Marking the 7, 8, 4, 5 lines
Marking the 7, 8, 4, 5 lines
-
 The completed dial plate for 52°N. Bedos de Celles (1790)
The completed dial plate for 52°N. Bedos de Celles (1790)
The method became well known when it was adopted by Waugh, as the construction method to be used for horizontal dials by Albert Waugh, in his 1973 book Sundials: their theory and construction.
References
- ^ Sawyer 2012, p. 35.
- ^ Waugh 1973, pp. 38–39.
Bibliography
- Sawyer, Fred (2012). "Horizontal Layouts 1–4". Compendium. 19 (11). Glastonbury, CT,USA: North American Sundial Society: 33–35.
- Waugh, Albert E. (1973). Sundials : their theory and construction. New York: Dover. pp. 38–39. ISBN 0486229475.
- Bédos de Celles, Francois (1760). "4-3". La Gnomonique pratique ou l'Art de tracer les cadrans solaires avec la plus grande précision (in French) (3 ed.). Paris. p. 459. Retrieved 12 July 2015.
- Dom François Bédos de Celles, L'art du facteur d'orgues (facsimile edition). Kassel / New York, Bärenreiter, 1963–65
- Ferguson, Charles, The Organ-Builder. Translation of Dom François Bédos de Celles' L'art du facteur d'orgues. Raleigh, NC: Sunbury Press, 1977
External links
- Extraits de L'Art du Facteur d'Orgues (in French)
- L'Art du Facteur d'Orgues on "L'Hydraule" (in French)
- IMSLP L'Art du Facteur d'Orgues.
- Video on YouTube Jean-Luc Perrot plays the Romance from l’Art du Facteur d’Orgues on the organ François-Henri Clicquot, Souvigny.


























 .
. .
.