Misplaced Pages

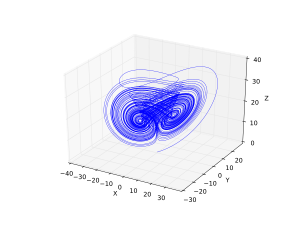
In the mathematics of dynamical systems, the double-scroll attractor (sometimes known as Chua's attractor) is a strange attractor observed from a physical electronic chaotic circuit (generally, Chua's circuit) with a single nonlinear resistor (see Chua's diode). The double-scroll system is often described by a system of three nonlinear ordinary differential equations and a 3-segment piecewise-linear equation (see Chua's equations). This makes the system easily simulated numerically and easily manifested physically due to Chua's circuits' simple design.

Using a Chua's circuit, this shape is viewed on an oscilloscope using the X, Y, and Z output signals of the circuit. This chaotic attractor is known as the double scroll because of its shape in three-dimensional space, which is similar to two saturn-like rings connected by swirling lines.

The attractor was first observed in simulations, then realized physically after Leon Chua invented the autonomous chaotic circuit which became known as Chua's circuit. The double-scroll attractor from the Chua circuit was rigorously proven to be chaotic through a number of Poincaré return maps of the attractor explicitly derived by way of compositions of the eigenvectors of the 3-dimensional state space.

Numerical analysis of the double-scroll attractor has shown that its geometrical structure is made up of an infinite number of fractal-like layers. Each cross section appears to be a fractal at all scales. Recently, there has also been reported the discovery of hidden attractors within the double scroll.

In 1999 Guanrong Chen (陈关荣) and Ueta proposed another double scroll chaotic attractor, called the Chen system or Chen attractor.

Chen attractor

The Chen system is defined as follows

${\displaystyle {\frac {dx(t)}{dt}}=a(y(t)-x(t))}$

${\displaystyle {\frac {dy(t)}{dt}}=(c-a)x(t)-x(t)z(t)+cy(t)}$

${\displaystyle {\frac {dz(t)}{dt}}=x(t)y(t)-bz(t)}$

Plots of Chen attractor can be obtained with the Runge-Kutta method:

parameters: a = 40, c = 28, b = 3

initial conditions: x(0) = -0.1, y(0) = 0.5, z(0) = -0.6

Other attractors

Multiscroll attractors also called n-scroll attractor include the Lu Chen attractor, the modified Chen chaotic attractor, PWL Duffing attractor, Rabinovich Fabrikant attractor, modified Chua chaotic attractor, that is, multiple scrolls in a single attractor.

Lu Chen attractor

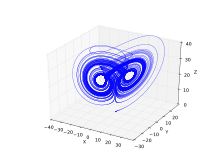
An extended Chen system with multiscroll was proposed by Jinhu Lu (吕金虎) and Guanrong Chen

Lu Chen system equation

${\displaystyle {\frac {dx(t)}{dt}}=a(y(t)-x(t))}$

${\displaystyle {\frac {dy(t)}{dt}}=x(t)-x(t)z(t)+cy(t)+u}$

${\displaystyle {\frac {dz(t)}{dt}}=x(t)y(t)-bz(t)}$

parameters：a = 36, c = 20, b = 3, u = -15.15

initial conditions：x(0) = .1, y(0) = .3, z(0) = -.6

Modified Lu Chen attractor

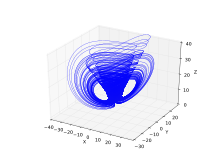
System equations:

${\displaystyle {\frac {dx(t)}{dt}}=a(y(t)-x(t)),}$

${\displaystyle {\frac {dy(t)}{dt}}=(c-a)x(t)-x(t)f+cy(t),}$

${\displaystyle {\frac {dz(t)}{dt}}=x(t)y(t)-bz(t)}$

In which

${\displaystyle f=d0z(t)+d1z(t-\tau )-d2\sin(z(t-\tau ))}$

params := a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2

initv := x(0) = 1, y(0) = 1, z(0) = 14

Modified Chua chaotic attractor

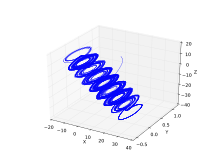
In 2001, Tang et al. proposed a modified Chua chaotic system

${\displaystyle {\frac {dx(t)}{dt}}=\alpha (y(t)-h)}$

${\displaystyle {\frac {dy(t)}{dt}}=x(t)-y(t)+z(t)}$

${\displaystyle {\frac {dz(t)}{dt}}=-\beta y(t)}$

In which

${\displaystyle h:=-b\sin \left({\frac {\pi x(t)}{2a}}+d\right)}$

params := alpha = 10.82, beta = 14.286, a = 1.3, b = .11, c = 7, d = 0

initv := x(0) = 1, y(0) = 1, z(0) = 0

PWL Duffing chaotic attractor

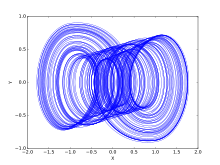
Aziz Alaoui investigated PWL Duffing equation in 2000:

PWL Duffing system:

${\displaystyle {\frac {dx(t)}{dt}}=y(t)}$

${\displaystyle {\frac {dy(t)}{dt}}=-m_{1}x(t)-(1/2(m_{0}-m_{1}))(|x(t)+1|-|x(t)-1|)-ey(t)+\gamma \cos(\omega t)}$

params := e = .25, gamma = .14+(1/20)i, m0 = -0.845e-1, m1 = .66, omega = 1; c := (.14+(1/20)i)，i=-25...25;

initv := x(0) = 0, y(0) = 0;

Modified Lorenz chaotic system

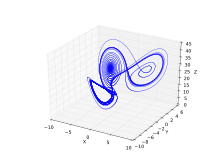
Miranda & Stone proposed a modified Lorenz system:

${\displaystyle {\frac {dx(t)}{dt}}=1/3*(-(a+1)x(t)+a-c+z(t)y(t))+((1-a)(x(t)^{2}-y(t)^{2})+(2(a+c-z(t)))x(t)y(t))}$${\displaystyle {\frac {1}{3{\sqrt {x(t)^{2}+y(t)^{2}}}}}}$

${\displaystyle {\frac {dy(t)}{dt}}=1/3((c-a-z(t))x(t)-(a+1)y(t))+((2(a-1))x(t)y(t)+(a+c-z(t))(x(t)^{2}-y(t)^{2}))}$${\displaystyle {\frac {1}{3{\sqrt {x(t)^{2}+y(t)^{2}}}}}}$

${\displaystyle {\frac {dz(t)}{dt}}=1/2(3x(t)^{2}y(t)-y(t)^{3})-bz(t)}$

parameters： a = 10, b = 8/3, c = 137/5;

initial conditions： x(0) = -8, y(0) = 4, z(0) = 10

Gallery

• Chen attractor
• parameters a = 35, c = 27, b = 2.8,x(0) = -.1, y(0) = .3, z(0) = -.6
• Lu Chen attractor
• Maple plot of N scroll attractor based on Chen with sine and tau
• 9 scroll modified Chua chaotic attractor
• xy plot of 9 scroll modified Chua chaotic attractor
• PWL Duffing chaotic attractor xy plot
• PWL Duffing chaotic attractor plot
• modified Lorenz attractor
• Rabinovich Fabrikant attractor xy plot

References

1. Matsumoto, Takashi (December 1984). "A Chaotic Attractor from Chua's Circuit" (PDF). IEEE Transactions on Circuits and Systems. CAS-31 (12). IEEE: 1055–1058. doi:10.1109/TCS.1984.1085459.
2. Chua, Leon; Motomasa Komoru; Takashi Matsumoto (November 1986). "The Double-Scroll Family" (PDF). IEEE Transactions on Circuits and Systems. CAS-33 (11).
3. Chua, Leon (2007). "Chua circuits". Scholarpedia. 2 (10): 1488. Bibcode:2007SchpJ...2.1488C. doi:10.4249/scholarpedia.1488.
4. Chua, Leon (2007). "Fractal Geometry of the Double-Scroll Attractor". Scholarpedia. 2 (10): 1488. Bibcode:2007SchpJ...2.1488C. doi:10.4249/scholarpedia.1488.
5. Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors" (PDF). Physics Letters A. 375 (23): 2230–2233. Bibcode:2011PhLA..375.2230L. doi:10.1016/j.physleta.2011.04.037.
6. Chen G., Ueta T. Yet another chaotic attractor. Journal of Bifurcation and Chaos, 1999 9:1465.
7. ^ CHEN, GUANRONG; UETA, TETSUSHI (July 1999). "Yet Another Chaotic Attractor". International Journal of Bifurcation and Chaos. 09 (7): 1465–1466. Bibcode:1999IJBC....9.1465C. doi:10.1142/s0218127499001024. ISSN 0218-1274.
8. 阎振亚著 《复杂非线性波的构造性理论及其应用》第17页 SCIENCEP 2007年
9. ^ Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 775–858. Bibcode:2006IJBC...16..775L. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
10. Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications" (PDF). International Journal of Bifurcation and Chaos. 16 (4): 793–794. Bibcode:2006IJBC...16..775L. CiteSeerX 10.1.1.927.4478. doi:10.1142/s0218127406015179. Retrieved 2012-02-16.
11. J. Lu, G. Chen p. 837
12. J.Liu and G Chen p834

External links

• The double-scroll attractor and Chua's circuit
• Lozi, R.; Pchelintsev, A.N. (2015). "A new reliable numerical method for computing chaotic solutions of dynamical systems: the Chen attractor case". International Journal of Bifurcation and Chaos. 25 (13): 1550187–1550412. Bibcode:2015IJBC...2550187L. doi:10.1142/S0218127415501874. S2CID 12339358.

v t e Chaos theory
Concepts	Core Attractor Bifurcation Fractal Limit set Lyapunov exponent Orbit Periodic point Phase space Anosov diffeomorphism Arnold tongue axiom A dynamical system Bifurcation diagram Box-counting dimension Correlation dimension Conservative system Ergodicity False nearest neighbors Hausdorff dimension Invariant measure Lyapunov stability Measure-preserving dynamical system Mixing Poincaré section Recurrence plot SRB measure Stable manifold Topological conjugacy Theorems Ergodic theorem Liouville's theorem Krylov–Bogolyubov theorem Poincaré–Bendixson theorem Poincaré recurrence theorem Stable manifold theorem Takens's theorem
Theoretical branches	Bifurcation theory Control of chaos Dynamical system Ergodic theory Quantum chaos Stability theory Synchronization of chaos
Chaotic maps (list)	Discrete Arnold's cat map Baker's map Complex quadratic map Coupled map lattice Duffing map Dyadic transformation Dynamical billiards outer Exponential map Gauss map Gingerbreadman map Hénon map Horseshoe map Ikeda map Interval exchange map Irrational rotation Kaplan–Yorke map Langton's ant Logistic map Standard map Tent map Tinkerbell map Zaslavskii map Continuous Double scroll attractor Duffing equation Lorenz system Lotka–Volterra equations Mackey–Glass equations Rabinovich–Fabrikant equations Rössler attractor Three-body problem Van der Pol oscillator
Physical systems	Chua's circuit Convection Double pendulum Elastic pendulum FPUT problem Hénon–Heiles system Kicked rotator Multiscroll attractor Population dynamics Swinging Atwood's machine Tilt-A-Whirl Weather
Chaos theorists	Michael Berry Rufus Bowen Mary Cartwright Chen Guanrong Leon O. Chua Mitchell Feigenbaum Peter Grassberger Celso Grebogi Martin Gutzwiller Brosl Hasslacher Michel Hénon Svetlana Jitomirskaya Bryna Kra Edward Norton Lorenz Aleksandr Lyapunov Benoît Mandelbrot Hee Oh Edward Ott Henri Poincaré Itamar Procaccia Mary Rees Otto Rössler David Ruelle Caroline Series Yakov Sinai Oleksandr Mykolayovych Sharkovsky Nina Snaith Floris Takens Audrey Terras Mary Tsingou Marcelo Viana Amie Wilkinson James A. Yorke Lai-Sang Young
Related articles	Butterfly effect Complexity Edge of chaos Predictability Santa Fe Institute

• Chaos theory