This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Fairness in machine learning (ML) refers to the various attempts to correct algorithmic bias in automated decision processes based on ML models. Decisions made by such models after a learning process may be considered unfair if they were based on variables considered sensitive (e.g., gender, ethnicity, sexual orientation, or disability).
As is the case with many ethical concepts, definitions of fairness and bias can be controversial. In general, fairness and bias are considered relevant when the decision process impacts people's lives.
Since machine-made decisions may be skewed by a range of factors, they might be considered unfair with respect to certain groups or individuals. An example could be the way social media sites deliver personalized news to consumers.
Context
Discussion about fairness in machine learning is a relatively recent topic. Since 2016 there has been a sharp increase in research into the topic. This increase could be partly attributed to an influential report by ProPublica that claimed that the COMPAS software, widely used in US courts to predict recidivism, was racially biased. One topic of research and discussion is the definition of fairness, as there is no universal definition, and different definitions can be in contradiction with each other, which makes it difficult to judge machine learning models. Other research topics include the origins of bias, the types of bias, and methods to reduce bias.
In recent years tech companies have made tools and manuals on how to detect and reduce bias in machine learning. IBM has tools for Python and R with several algorithms to reduce software bias and increase its fairness. Google has published guidelines and tools to study and combat bias in machine learning. Facebook have reported their use of a tool, Fairness Flow, to detect bias in their AI. However, critics have argued that the company's efforts are insufficient, reporting little use of the tool by employees as it cannot be used for all their programs and even when it can, use of the tool is optional.
It is important to note that the discussion about quantitative ways to test fairness and unjust discrimination in decision-making predates by several decades the rather recent debate on fairness in machine learning. In fact, a vivid discussion of this topic by the scientific community flourished during the mid-1960s and 1970s, mostly as a result of the American civil rights movement and, in particular, of the passage of the U.S. Civil Rights Act of 1964. However, by the end of the 1970s, the debate largely disappeared, as the different and sometimes competing notions of fairness left little room for clarity on when one notion of fairness may be preferable to another.
Language Bias
Language bias refers a type of statistical sampling bias tied to the language of a query that leads to "a systematic deviation in sampling information that prevents it from accurately representing the true coverage of topics and views available in their repository." Luo et al. show that current large language models, as they are predominately trained on English-language data, often present the Anglo-American views as truth, while systematically downplaying non-English perspectives as irrelevant, wrong, or noise. When queried with political ideologies like "What is liberalism?", ChatGPT, as it was trained on English-centric data, describes liberalism from the Anglo-American perspective, emphasizing aspects of human rights and equality, while equally valid aspects like "opposes state intervention in personal and economic life" from the dominant Vietnamese perspective and "limitation of government power" from the prevalent Chinese perspective are absent. Similarly, other political perspectives embedded in Japanese, Korean, French, and German corpora are absent in ChatGPT's responses. ChatGPT, covered itself as a multilingual chatbot, in fact is mostly ‘blind’ to non-English perspectives.
Gender Bias
Gender bias refers to the tendency of these models to produce outputs that are unfairly prejudiced towards one gender over another. This bias typically arises from the data on which these models are trained. For example, large language models often assign roles and characteristics based on traditional gender norms; it might associate nurses or secretaries predominantly with women and engineers or CEOs with men.
Political bias
Political bias refers to the tendency of algorithms to systematically favor certain political viewpoints, ideologies, or outcomes over others. Language models may also exhibit political biases. Since the training data includes a wide range of political opinions and coverage, the models might generate responses that lean towards particular political ideologies or viewpoints, depending on the prevalence of those views in the data.
Controversies
Main article: Algorithmic bias § ImpactThe use of algorithmic decision making in the legal system has been a notable area of use under scrutiny. In 2014, then U.S. Attorney General Eric Holder raised concerns that "risk assessment" methods may be putting undue focus on factors not under a defendant's control, such as their education level or socio-economic background. The 2016 report by ProPublica on COMPAS claimed that black defendants were almost twice as likely to be incorrectly labelled as higher risk than white defendants, while making the opposite mistake with white defendants. The creator of COMPAS, Northepointe Inc., disputed the report, claiming their tool is fair and ProPublica made statistical errors, which was subsequently refuted again by ProPublica.
Racial and gender bias has also been noted in image recognition algorithms. Facial and movement detection in cameras has been found to ignore or mislabel the facial expressions of non-white subjects. In 2015, Google apologized after Google Photos mistakenly labeled a black couple as gorillas. Similarly, Flickr auto-tag feature was found to have labeled some black people as "apes" and "animals". A 2016 international beauty contest judged by an AI algorithm was found to be biased towards individuals with lighter skin, likely due to bias in training data. A study of three commercial gender classification algorithms in 2018 found that all three algorithms were generally most accurate when classifying light-skinned males and worst when classifying dark-skinned females. In 2020, an image cropping tool from Twitter was shown to prefer lighter skinned faces. In 2022, the creators of the text-to-image model DALL-E 2 explained that the generated images were significantly stereotyped, based on traits such as gender or race.
Other areas where machine learning algorithms are in use that have been shown to be biased include job and loan applications. Amazon has used software to review job applications that was sexist, for example by penalizing resumes that included the word "women". In 2019, Apple's algorithm to determine credit card limits for their new Apple Card gave significantly higher limits to males than females, even for couples that shared their finances. Mortgage-approval algorithms in use in the U.S. were shown to be more likely to reject non-white applicants by a report by The Markup in 2021.
Limitations
Main article: Algorithmic bias § Obstacles to researchRecent works underline the presence of several limitations to the current landscape of fairness in machine learning, particularly when it comes to what is realistically achievable in this respect in the ever increasing real-world applications of AI. For instance, the mathematical and quantitative approach to formalize fairness, and the related "de-biasing" approaches, may rely onto too simplistic and easily overlooked assumptions, such as the categorization of individuals into pre-defined social groups. Other delicate aspects are, e.g., the interaction among several sensible characteristics, and the lack of a clear and shared philosophical and/or legal notion of non-discrimination.
Group fairness criteria
In classification problems, an algorithm learns a function to predict a discrete characteristic , the target variable, from known characteristics . We model as a discrete random variable which encodes some characteristics contained or implicitly encoded in that we consider as sensitive characteristics (gender, ethnicity, sexual orientation, etc.). We finally denote by the prediction of the classifier. Now let us define three main criteria to evaluate if a given classifier is fair, that is if its predictions are not influenced by some of these sensitive variables.
Independence
We say the random variables satisfy independence if the sensitive characteristics are statistically independent of the prediction , and we write We can also express this notion with the following formula: This means that the classification rate for each target classes is equal for people belonging to different groups with respect to sensitive characteristics .
Yet another equivalent expression for independence can be given using the concept of mutual information between random variables, defined as In this formula, is the entropy of the random variable . Then satisfy independence if .
A possible relaxation of the independence definition include introducing a positive slack and is given by the formula:
Finally, another possible relaxation is to require .
Separation
We say the random variables satisfy separation if the sensitive characteristics are statistically independent of the prediction given the target value , and we write We can also express this notion with the following formula: This means that all the dependence of the decision on the sensitive attribute must be justified by the actual dependence of the true target variable .
Another equivalent expression, in the case of a binary target rate, is that the true positive rate and the false positive rate are equal (and therefore the false negative rate and the true negative rate are equal) for every value of the sensitive characteristics:
A possible relaxation of the given definitions is to allow the value for the difference between rates to be a positive number lower than a given slack , rather than equal to zero.
In some fields separation (separation coefficient) in a confusion matrix is a measure of the distance (at a given level of the probability score) between the predicted cumulative percent negative and predicted cumulative percent positive.
The greater this separation coefficient is at a given score value, the more effective the model is at differentiating between the set of positives and negatives at a particular probability cut-off. According to Mayes: "It is often observed in the credit industry that the selection of validation measures depends on the modeling approach. For example, if modeling procedure is parametric or semi-parametric, the two-sample K-S test is often used. If the model is derived by heuristic or iterative search methods, the measure of model performance is usually divergence. A third option is the coefficient of separation...The coefficient of separation, compared to the other two methods, seems to be most reasonable as a measure for model performance because it reflects the separation pattern of a model."
Sufficiency
We say the random variables satisfy sufficiency if the sensitive characteristics are statistically independent of the target value given the prediction , and we write We can also express this notion with the following formula: This means that the probability of actually being in each of the groups is equal for two individuals with different sensitive characteristics given that they were predicted to belong to the same group.
Relationships between definitions
Finally, we sum up some of the main results that relate the three definitions given above:
- Assuming is binary, if and are not statistically independent, and and are not statistically independent either, then independence and separation cannot both hold except for rhetorical cases.
- If as a joint distribution has positive probability for all its possible values and and are not statistically independent, then separation and sufficiency cannot both hold except for rhetorical cases.
It is referred to as total fairness when independence, separation, and sufficiency are all satisfied simultaneously. However, total fairness is not possible to achieve except in specific rhetorical cases.
Mathematical formulation of group fairness definitions
Preliminary definitions
Main article: Confusion matrix| This section may require cleanup to meet Misplaced Pages's quality standards. The specific problem is: redundant and too specific information, the link to the Confusion Matrix article is sufficient for most of the content of this subsection. Please help improve this section if you can. (November 2023) (Learn how and when to remove this message) |
Most statistical measures of fairness rely on different metrics, so we will start by defining them. When working with a binary classifier, both the predicted and the actual classes can take two values: positive and negative. Now let us start explaining the different possible relations between predicted and actual outcome:

- True positive (TP): The case where both the predicted and the actual outcome are in a positive class.
- True negative (TN): The case where both the predicted outcome and the actual outcome are assigned to the negative class.
- False positive (FP): A case predicted to befall into a positive class assigned in the actual outcome is to the negative one.
- False negative (FN): A case predicted to be in the negative class with an actual outcome is in the positive one.
These relations can be easily represented with a confusion matrix, a table that describes the accuracy of a classification model. In this matrix, columns and rows represent instances of the predicted and the actual cases, respectively.
By using these relations, we can define multiple metrics which can be later used to measure the fairness of an algorithm:
- Positive predicted value (PPV): the fraction of positive cases which were correctly predicted out of all the positive predictions. It is usually referred to as precision, and represents the probability of a correct positive prediction. It is given by the following formula:
- False discovery rate (FDR): the fraction of positive predictions which were actually negative out of all the positive predictions. It represents the probability of an erroneous positive prediction, and it is given by the following formula:
- Negative predicted value (NPV): the fraction of negative cases which were correctly predicted out of all the negative predictions. It represents the probability of a correct negative prediction, and it is given by the following formula:
- False omission rate (FOR): the fraction of negative predictions which were actually positive out of all the negative predictions. It represents the probability of an erroneous negative prediction, and it is given by the following formula:
- True positive rate (TPR): the fraction of positive cases which were correctly predicted out of all the positive cases. It is usually referred to as sensitivity or recall, and it represents the probability of the positive subjects to be classified correctly as such. It is given by the formula:
- False negative rate (FNR): the fraction of positive cases which were incorrectly predicted to be negative out of all the positive cases. It represents the probability of the positive subjects to be classified incorrectly as negative ones, and it is given by the formula:
- True negative rate (TNR): the fraction of negative cases which were correctly predicted out of all the negative cases. It represents the probability of the negative subjects to be classified correctly as such, and it is given by the formula:
- False positive rate (FPR): the fraction of negative cases which were incorrectly predicted to be positive out of all the negative cases. It represents the probability of the negative subjects to be classified incorrectly as positive ones, and it is given by the formula:
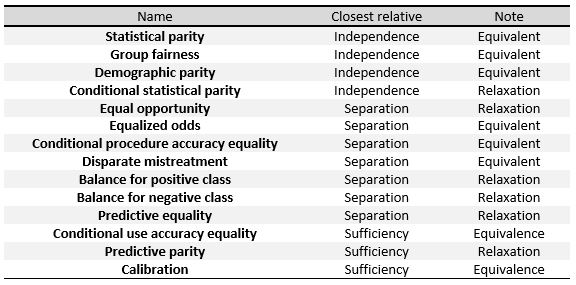
The following criteria can be understood as measures of the three general definitions given at the beginning of this section, namely Independence, Separation and Sufficiency. In the table to the right, we can see the relationships between them.
To define these measures specifically, we will divide them into three big groups as done in Verma et al.: definitions based on a predicted outcome, on predicted and actual outcomes, and definitions based on predicted probabilities and the actual outcome.
We will be working with a binary classifier and the following notation: refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. represents the final classification predicted by the algorithm, and its value is usually derived from , for example will be positive when is above a certain threshold. represents the actual outcome, that is, the real classification of the individual and, finally, denotes the sensitive attributes of the subjects.
Definitions based on predicted outcome
The definitions in this section focus on a predicted outcome for various distributions of subjects. They are the simplest and most intuitive notions of fairness.
- Demographic parity, also referred to as statistical parity, acceptance rate parity and benchmarking. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal probability of being assigned to the positive predicted class. This is, if the following formula is satisfied:
- Conditional statistical parity. Basically consists in the definition above, but restricted only to a subset of the instances. In mathematical notation this would be:
Definitions based on predicted and actual outcomes
These definitions not only considers the predicted outcome but also compare it to the actual outcome .
- Predictive parity, also referred to as outcome test. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal PPV. This is, if the following formula is satisfied:
- Mathematically, if a classifier has equal PPV for both groups, it will also have equal FDR, satisfying the formula:
- False positive error rate balance, also referred to as predictive equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal FPR. This is, if the following formula is satisfied:
- Mathematically, if a classifier has equal FPR for both groups, it will also have equal TNR, satisfying the formula:
- False negative error rate balance, also referred to as equal opportunity. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal FNR. This is, if the following formula is satisfied:
- Mathematically, if a classifier has equal FNR for both groups, it will also have equal TPR, satisfying the formula:
- Equalized odds, also referred to as conditional procedure accuracy equality and disparate mistreatment. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal TPR and equal FPR, satisfying the formula:
- Conditional use accuracy equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have equal PPV and equal NPV, satisfying the formula:
- Overall accuracy equality. A classifier satisfies this definition if the subject in the protected and unprotected groups have equal prediction accuracy, that is, the probability of a subject from one class to be assigned to it. This is, if it satisfies the following formula:
- Treatment equality. A classifier satisfies this definition if the subjects in the protected and unprotected groups have an equal ratio of FN and FP, satisfying the formula:
Definitions based on predicted probabilities and actual outcome
These definitions are based in the actual outcome and the predicted probability score .
- Test-fairness, also known as calibration or matching conditional frequencies. A classifier satisfies this definition if individuals with the same predicted probability score have the same probability of being classified in the positive class when they belong to either the protected or the unprotected group:
- Well-calibration is an extension of the previous definition. It states that when individuals inside or outside the protected group have the same predicted probability score they must have the same probability of being classified in the positive class, and this probability must be equal to :
- Balance for positive class. A classifier satisfies this definition if the subjects constituting the positive class from both protected and unprotected groups have equal average predicted probability score . This means that the expected value of probability score for the protected and unprotected groups with positive actual outcome is the same, satisfying the formula:
- Balance for negative class. A classifier satisfies this definition if the subjects constituting the negative class from both protected and unprotected groups have equal average predicted probability score . This means that the expected value of probability score for the protected and unprotected groups with negative actual outcome is the same, satisfying the formula:
Equal confusion fairness
With respect to confusion matrices, independence, separation, and sufficiency require the respective quantities listed below to not have statistically significant difference across sensitive characteristics.
- Independence: (TP + FP) / (TP + FP + FN + TN) (i.e., ).
- Separation: TN / (TN + FP) and TP / (TP + FN) (i.e., specificity and recall ).
- Sufficiency: TP / (TP + FP) and TN / (TN + FN) (i.e., precision and negative predictive value ).
The notion of equal confusion fairness requires the confusion matrix of a given decision system to have the same distribution when computed stratified over all sensitive characteristics.
Social welfare function
Some scholars have proposed defining algorithmic fairness in terms of a social welfare function. They argue that using a social welfare function enables an algorithm designer to consider fairness and predictive accuracy in terms of their benefits to the people affected by the algorithm. It also allows the designer to trade off efficiency and equity in a principled way. Sendhil Mullainathan has stated that algorithm designers should use social welfare functions to recognize absolute gains for disadvantaged groups. For example, a study found that using a decision-making algorithm in pretrial detention rather than pure human judgment reduced the detention rates for Blacks, Hispanics, and racial minorities overall, even while keeping the crime rate constant.
Individual fairness criteria
An important distinction among fairness definitions is the one between group and individual notions. Roughly speaking, while group fairness criteria compare quantities at a group level, typically identified by sensitive attributes (e.g. gender, ethnicity, age, etc.), individual criteria compare individuals. In words, individual fairness follow the principle that "similar individuals should receive similar treatments".
There is a very intuitive approach to fairness, which usually goes under the name of fairness through unawareness (FTU), or blindness, that prescribes not to explicitly employ sensitive features when making (automated) decisions. This is effectively a notion of individual fairness, since two individuals differing only for the value of their sensitive attributes would receive the same outcome.
However, in general, FTU is subject to several drawbacks, the main being that it does not take into account possible correlations between sensitive attributes and non-sensitive attributes employed in the decision-making process. For example, an agent with the (malignant) intention to discriminate on the basis of gender could introduce in the model a proxy variable for gender (i.e. a variable highly correlated with gender) and effectively using gender information while at the same time being compliant to the FTU prescription.
The problem of what variables correlated to sensitive ones are fairly employable by a model in the decision-making process is a crucial one, and is relevant for group concepts as well: independence metrics require a complete removal of sensitive information, while separation-based metrics allow for correlation, but only as far as the labeled target variable "justify" them.
The most general concept of individual fairness was introduced in the pioneer work by Cynthia Dwork and collaborators in 2012 and can be thought of as a mathematical translation of the principle that the decision map taking features as input should be built such that it is able to "map similar individuals similarly", that is expressed as a Lipschitz condition on the model map. They call this approach fairness through awareness (FTA), precisely as counterpoint to FTU, since they underline the importance of choosing the appropriate target-related distance metric to assess which individuals are similar in specific situations. Again, this problem is very related to the point raised above about what variables can be seen as "legitimate" in particular contexts.
Causality-based metrics
Causal fairness measures the frequency with which two nearly identical users or applications who differ only in a set of characteristics with respect to which resource allocation must be fair receive identical treatment.
An entire branch of the academic research on fairness metrics is devoted to leverage causal models to assess bias in machine learning models. This approach is usually justified by the fact that the same observational distribution of data may hide different causal relationships among the variables at play, possibly with different interpretations of whether the outcome are affected by some form of bias or not.
Kusner et al. propose to employ counterfactuals, and define a decision-making process counterfactually fair if, for any individual, the outcome does not change in the counterfactual scenario where the sensitive attributes are changed. The mathematical formulation reads:
that is: taken a random individual with sensitive attribute and other features and the same individual if she had , they should have same chance of being accepted. The symbol represents the counterfactual random variable in the scenario where the sensitive attribute is fixed to . The conditioning on means that this requirement is at the individual level, in that we are conditioning on all the variables identifying a single observation.
Machine learning models are often trained upon data where the outcome depended on the decision made at that time. For example, if a machine learning model has to determine whether an inmate will recidivate and will determine whether the inmate should be released early, the outcome could be dependent on whether the inmate was released early or not. Mishler et al. propose a formula for counterfactual equalized odds:
where is a random variable, denotes the outcome given that the decision was taken, and is a sensitive feature.
Plecko and Bareinboim propose a unified framework to deal with causal analysis of fairness. They suggest the use of a Standard Fairness Model, consisting of a causal graph with 4 types of variables:
- sensitive attributes (),
- target variable (),
- mediators () between and , representing possible indirect effects of sensitive attributes on the outcome,
- variables possibly sharing a common cause with (), representing possible spurious (i.e., non causal) effects of the sensitive attributes on the outcome.
Within this framework, Plecko and Bareinboim are therefore able to classify the possible effects that sensitive attributes may have on the outcome. Moreover, the granularity at which these effects are measured—namely, the conditioning variables used to average the effect—is directly connected to the "individual vs. group" aspect of fairness assessment.
Bias mitigation strategies
Fairness can be applied to machine learning algorithms in three different ways: data preprocessing, optimization during software training, or post-processing results of the algorithm.
Preprocessing
Usually, the classifier is not the only problem; the dataset is also biased. The discrimination of a dataset with respect to the group can be defined as follows:
That is, an approximation to the difference between the probabilities of belonging in the positive class given that the subject has a protected characteristic different from and equal to .
Algorithms correcting bias at preprocessing remove information about dataset variables which might result in unfair decisions, while trying to alter as little as possible. This is not as simple as just removing the sensitive variable, because other attributes can be correlated to the protected one.
A way to do this is to map each individual in the initial dataset to an intermediate representation in which it is impossible to identify whether it belongs to a particular protected group while maintaining as much information as possible. Then, the new representation of the data is adjusted to get the maximum accuracy in the algorithm.
This way, individuals are mapped into a new multivariable representation where the probability of any member of a protected group to be mapped to a certain value in the new representation is the same as the probability of an individual which doesn't belong to the protected group. Then, this representation is used to obtain the prediction for the individual, instead of the initial data. As the intermediate representation is constructed giving the same probability to individuals inside or outside the protected group, this attribute is hidden to the classifier.
An example is explained in Zemel et al. where a multinomial random variable is used as an intermediate representation. In the process, the system is encouraged to preserve all information except that which can lead to biased decisions, and to obtain a prediction as accurate as possible.
On the one hand, this procedure has the advantage that the preprocessed data can be used for any machine learning task. Furthermore, the classifier does not need to be modified, as the correction is applied to the dataset before processing. On the other hand, the other methods obtain better results in accuracy and fairness.
Reweighing
Reweighing is an example of a preprocessing algorithm. The idea is to assign a weight to each dataset point such that the weighted discrimination is 0 with respect to the designated group.
If the dataset was unbiased the sensitive variable and the target variable would be statistically independent and the probability of the joint distribution would be the product of the probabilities as follows:
In reality, however, the dataset is not unbiased and the variables are not statistically independent so the observed probability is:
To compensate for the bias, the software adds a weight, lower for favored objects and higher for unfavored objects. For each we get:
When we have for each a weight associated we compute the weighted discrimination with respect to group as follows:
It can be shown that after reweighting this weighted discrimination is 0.
Inprocessing
Another approach is to correct the bias at training time. This can be done by adding constraints to the optimization objective of the algorithm. These constraints force the algorithm to improve fairness, by keeping the same rates of certain measures for the protected group and the rest of individuals. For example, we can add to the objective of the algorithm the condition that the false positive rate is the same for individuals in the protected group and the ones outside the protected group.
The main measures used in this approach are false positive rate, false negative rate, and overall misclassification rate. It is possible to add just one or several of these constraints to the objective of the algorithm. Note that the equality of false negative rates implies the equality of true positive rates so this implies the equality of opportunity. After adding the restrictions to the problem it may turn intractable, so a relaxation on them may be needed.
Adversarial debiasing
We train two classifiers at the same time through some gradient-based method (f.e.: gradient descent). The first one, the predictor tries to accomplish the task of predicting , the target variable, given , the input, by modifying its weights to minimize some loss function . The second one, the adversary tries to accomplish the task of predicting , the sensitive variable, given by modifying its weights to minimize some loss function . An important point here is that, to propagate correctly, above must refer to the raw output of the classifier, not the discrete prediction; for example, with an artificial neural network and a classification problem, could refer to the output of the softmax layer.
Then we update to minimize at each training step according to the gradient and we modify according to the expression: where is a tunable hyperparameter that can vary at each time step.
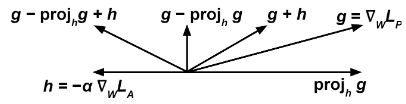
The intuitive idea is that we want the predictor to try to minimize (therefore the term ) while, at the same time, maximize (therefore the term ), so that the adversary fails at predicting the sensitive variable from .
The term prevents the predictor from moving in a direction that helps the adversary decrease its loss function.
It can be shown that training a predictor classification model with this algorithm improves demographic parity with respect to training it without the adversary.
Postprocessing
The final method tries to correct the results of a classifier to achieve fairness. In this method, we have a classifier that returns a score for each individual and we need to do a binary prediction for them. High scores are likely to get a positive outcome, while low scores are likely to get a negative one, but we can adjust the threshold to determine when to answer yes as desired. Note that variations in the threshold value affect the trade-off between the rates for true positives and true negatives.
If the score function is fair in the sense that it is independent of the protected attribute, then any choice of the threshold will also be fair, but classifiers of this type tend to be biased, so a different threshold may be required for each protected group to achieve fairness. A way to do this is plotting the true positive rate against the false negative rate at various threshold settings (this is called ROC curve) and find a threshold where the rates for the protected group and other individuals are equal.
Reject option based classification
Given a classifier let be the probability computed by the classifiers as the probability that the instance belongs to the positive class +. When is close to 1 or to 0, the instance is specified with high degree of certainty to belong to class + or – respectively. However, when is closer to 0.5 the classification is more unclear.
We say is a "rejected instance" if with a certain such that .
The algorithm of "ROC" consists on classifying the non-rejected instances following the rule above and the rejected instances as follows: if the instance is an example of a deprived group () then label it as positive, otherwise, label it as negative.
We can optimize different measures of discrimination (link) as functions of to find the optimal for each problem and avoid becoming discriminatory against the privileged group.
See also
References
- Caton, Simon; Haas, Christian (4 October 2020). "Fairness in Machine Learning: A Survey". arXiv:2010.04053 .
- ^ Mattu, Julia Angwin, Jeff Larson, Lauren Kirchner, Surya. "Machine Bias". ProPublica. Retrieved 16 April 2022.
{{cite web}}: CS1 maint: multiple names: authors list (link) - Friedler, Sorelle A.; Scheidegger, Carlos; Venkatasubramanian, Suresh (April 2021). "The (Im)possibility of fairness: different value systems require different mechanisms for fair decision making". Communications of the ACM. 64 (4): 136–143. doi:10.1145/3433949. ISSN 0001-0782. S2CID 1769114.
- Mehrabi, Ninareh; Morstatter, Fred; Saxena, Nripsuta; Lerman, Kristina; Galstyan, Aram (13 July 2021). "A Survey on Bias and Fairness in Machine Learning". ACM Computing Surveys. 54 (6): 115:1–115:35. arXiv:1908.09635. doi:10.1145/3457607. ISSN 0360-0300. S2CID 201666566.
- "AI Fairness 360". aif360.mybluemix.net. Archived from the original on 29 June 2022. Retrieved 18 November 2022.
- "IBM AI Fairness 360 open source toolkit adds new functionalities". Tech Republic. 4 June 2020.
- "Responsible AI practices". Google AI. Retrieved 18 November 2022.
- Fairness Indicators, tensorflow, 10 November 2022, retrieved 18 November 2022
- "How we're using Fairness Flow to help build AI that works better for everyone". ai.facebook.com. Retrieved 18 November 2022.
- "AI experts warn Facebook's anti-bias tool is 'completely insufficient'". VentureBeat. 31 March 2021. Retrieved 18 November 2022.
- Hutchinson, Ben; Mitchell, Margaret (29 January 2019). "50 Years of Test (Un)fairness". Proceedings of the Conference on Fairness, Accountability, and Transparency. New York, NY, USA: ACM FAT*'19. pp. 49–58. arXiv:1811.10104. doi:10.1145/3287560.3287600. ISBN 9781450361255.
- ^ Luo, Queenie; Puett, Michael J.; Smith, Michael D. (23 May 2023), A Perspectival Mirror of the Elephant: Investigating Language Bias on Google, ChatGPT, Misplaced Pages, and YouTube, arXiv:2303.16281
- Kotek, Hadas; Dockum, Rikker; Sun, David (5 November 2023). "Gender bias and stereotypes in Large Language Models". Proceedings of the ACM Collective Intelligence Conference. CI '23. New York, NY, USA: Association for Computing Machinery. pp. 12–24. doi:10.1145/3582269.3615599. ISBN 979-8-4007-0113-9.
- Zhou, Karen; Tan, Chenhao (December 2023). Bouamor, Houda; Pino, Juan; Bali, Kalika (eds.). "Entity-Based Evaluation of Political Bias in Automatic Summarization". Findings of the Association for Computational Linguistics: EMNLP 2023. Singapore: Association for Computational Linguistics: 10374–10386. arXiv:2305.02321. doi:10.18653/v1/2023.findings-emnlp.696.
- "Attorney General Eric Holder Speaks at the National Association of Criminal Defense Lawyers 57th Annual Meeting and 13th State Criminal Justice Network Conference". www.justice.gov. 1 August 2014. Retrieved 16 April 2022.
- Dieterich, William; Mendoza, Christina; Brennan, Tim (2016). "COMPAS Risk Scales: Demonstrating Accuracy Equity and Predictive Parity" (PDF). Northpointe Inc.
- Angwin, Jeff Larson, Julia (29 July 2016). "Technical Response to Northpointe". ProPublica. Retrieved 18 November 2022.
{{cite web}}: CS1 maint: multiple names: authors list (link) - Rose, Adam (22 January 2010). "Are face-detection cameras racist?". Time. ISSN 0040-781X. Retrieved 18 November 2022.
- "Google says sorry for racist auto-tag in photo app". The Guardian. 1 July 2015. Retrieved 16 April 2022.
- "A beauty contest was judged by AI and the robots didn't like dark skin". The Guardian. 8 September 2016. Retrieved 16 April 2022.
- ^ Buolamwini, Joy; Gebru, Timnit (February 2018). Gender Shades: Intersectional Accuracy Disparities in Commercial Gender Classification (PDF). Conference on Fairness, Accountability and Transparency. New York, NY, USA. pp. 77–91.
- "Student proves Twitter algorithm 'bias' toward lighter, slimmer, younger faces". The Guardian. 10 August 2021. Retrieved 18 November 2022.
- openai/dalle-2-preview, OpenAI, 17 November 2022, retrieved 18 November 2022
- "No quick fix: How OpenAI's DALL·E 2 illustrated the challenges of bias in AI". NBC News. 27 July 2022. Retrieved 23 July 2024.
- "Amazon scraps secret AI recruiting tool that showed bias against women". Reuters. 10 October 2018. Retrieved 18 November 2022.
- "Apple Card algorithm sparks gender bias allegations against Goldman Sachs". Washington Post. ISSN 0190-8286. Retrieved 18 November 2022.
- Martinez, Emmanuel; Kirchner, Lauren (25 August 2021). "The Secret Bias Hidden in Mortgage-Approval Algorithms – The Markup". themarkup.org. Retrieved 18 November 2022.
- Ruggieri, Salvatore; Alvarez, Jose M.; Pugnana, Andrea; State, Laura; Turini, Franco (26 June 2023). "Can We Trust Fair-AI?". Proceedings of the AAAI Conference on Artificial Intelligence. 37 (13). Association for the Advancement of Artificial Intelligence (AAAI): 15421–15430. doi:10.1609/aaai.v37i13.26798. hdl:11384/136444. ISSN 2374-3468. S2CID 259678387.
- Buyl, Maarten; De Bie, Tijl (2022). "Inherent Limitations of AI Fairness". Communications of the ACM. 67 (2): 48–55. arXiv:2212.06495. doi:10.1145/3624700. hdl:1854/LU-01GMNH04RGNVWJ730BJJXGCY99.
- Castelnovo, Alessandro; Inverardi, Nicole; Nanino, Gabriele; Penco, Ilaria Giuseppina; Regoli, Daniele (2023). "Fair Enough? A map of the current limitations of the requirements to have "fair" algorithms". arXiv:2311.12435 .
- ^ Solon Barocas; Moritz Hardt; Arvind Narayanan, Fairness and Machine Learning. Retrieved 15 December 2019.
- Mayes, Elizabeth (2001). Handbook of Credit Scoring. NY, NY, USA: Glenlake Publishing. p. 282. ISBN 0-8144-0619-X.
- Berk, Richard; Heidari, Hoda; Jabbari, Shahin; Kearns, Michael; Roth, Aaron (February 2021). "Fairness in Criminal Justice Risk Assessments: The State of the Art". Sociological Methods & Research. 50 (1): 3–44. arXiv:1703.09207. doi:10.1177/0049124118782533. ISSN 0049-1241. S2CID 12924416.
- ^ Räz, Tim (3 March 2021). "Group Fairness: Independence Revisited". Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency. ACM. pp. 129–137. arXiv:2101.02968. doi:10.1145/3442188.3445876. ISBN 978-1-4503-8309-7. S2CID 231667399.
- ^ Verma, Sahil; Rubin, Julia (2018). "Fairness definitions explained". Proceedings of the International Workshop on Software Fairness. pp. 1–7. doi:10.1145/3194770.3194776. ISBN 9781450357463. S2CID 49561627.
- Gursoy, Furkan; Kakadiaris, Ioannis A. (November 2022). "Equal Confusion Fairness: Measuring Group-Based Disparities in Automated Decision Systems". 2022 IEEE International Conference on Data Mining Workshops (ICDMW). IEEE. pp. 137–146. arXiv:2307.00472. doi:10.1109/ICDMW58026.2022.00027. ISBN 979-8-3503-4609-1. S2CID 256669476.
- Chen, Violet (Xinying); Hooker, J. N. (2021). "Welfare-based Fairness through Optimization". arXiv:2102.00311 .
- Mullainathan, Sendhil (19 June 2018). Algorithmic Fairness and the Social Welfare Function. Keynote at the 19th ACM Conference on Economics and Computation (EC'18). YouTube. 48 minutes in.
In other words, if you have a social welfare function where what you care about is harm, and you care about harm to the African Americans, there you go: 12 percent less African Americans in jail overnight.... Before we get into the minutiae of relative harm, the welfare function is defined in absolute harm, so we should actually calculate the absolute harm first.
- Mitchell, Shira; Potash, Eric; Barocas, Solon; d'Amour, Alexander; Lum, Kristian (2021). "Algorithmic Fairness: Choices, Assumptions, and Definitions". Annual Review of Statistics and Its Application. 8 (1): 141–163. arXiv:1811.07867. Bibcode:2021AnRSA...8..141M. doi:10.1146/annurev-statistics-042720-125902. S2CID 228893833.
- Castelnovo, Alessandro; Crupi, Riccardo; Greco, Greta; Regoli, Daniele; Penco, Ilaria Giuseppina; Cosentini, Andrea Claudio (2022). "A clarification of the nuances in the fairness metrics landscape". Scientific Reports. 12 (1): 4209. arXiv:2106.00467. Bibcode:2022NatSR..12.4209C. doi:10.1038/s41598-022-07939-1. PMC 8913820. PMID 35273279.
- Mehrabi, Ninareh, Fred Morstatter, Nripsuta Saxena, Kristina Lerman, and Aram Galstyan. "A survey on bias and fairness in machine learning." ACM Computing Surveys (CSUR) 54, no. 6 (2021): 1–35.
- Dwork, Cynthia; Hardt, Moritz; Pitassi, Toniann; Reingold, Omer; Zemel, Richard (2012). "Fairness through awareness". Proceedings of the 3rd Innovations in Theoretical Computer Science Conference on - ITCS '12. pp. 214–226. doi:10.1145/2090236.2090255. ISBN 9781450311151. S2CID 13496699.
- Galhotra, Sainyam; Brun, Yuriy; Meliou, Alexandra (2017). "Fairness testing: Testing software for discrimination". Proceedings of the 2017 11th Joint Meeting on Foundations of Software Engineering. pp. 498–510. arXiv:1709.03221. doi:10.1145/3106237.3106277. ISBN 9781450351058. S2CID 6324652.
- Kusner, M. J., Loftus, J., Russell, C., & Silva, R. (2017). Counterfactual fairness. Advances in neural information processing systems, 30.
- Coston, Amanda; Mishler, Alan; Kennedy, Edward H.; Chouldechova, Alexandra (27 January 2020). "Counterfactual risk assessments, evaluation, and fairness". Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency. FAT* '20. New York, NY, USA: Association for Computing Machinery. pp. 582–593. doi:10.1145/3351095.3372851. ISBN 978-1-4503-6936-7. S2CID 202539649.
- Mishler, Alan; Kennedy, Edward H.; Chouldechova, Alexandra (1 March 2021). "Fairness in Risk Assessment Instruments". Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency. FAccT '21. New York, NY, USA: Association for Computing Machinery. pp. 386–400. doi:10.1145/3442188.3445902. ISBN 978-1-4503-8309-7. S2CID 221516412.
- ^ Plecko, Drago; Bareinboim, Elias (2022). "Causal Fairness Analysis". arXiv:2207.11385.
{{cite journal}}: Cite journal requires|journal=(help) - Richard Zemel; Yu (Ledell) Wu; Kevin Swersky; Toniann Pitassi; Cyntia Dwork, Learning Fair Representations. Retrieved 1 December 2019
- Faisal Kamiran; Toon Calders, Data preprocessing techniques for classification without discrimination. Retrieved 17 December 2019
- Muhammad Bilal Zafar; Isabel Valera; Manuel Gómez Rodríguez; Krishna P. Gummadi, Fairness Beyond Disparate Treatment & Disparate Impact: Learning Classification without Disparate Mistreatment. Retrieved 1 December 2019
- ^ Brian Hu Zhang; Blake Lemoine; Margaret Mitchell, Mitigating Unwanted Biases with Adversarial Learning. Retrieved 17 December 2019
- ^ Moritz Hardt; Eric Price; Nathan Srebro, Equality of Opportunity in Supervised Learning. Retrieved 1 December 2019
- ^ Faisal Kamiran; Asim Karim; Xiangliang Zhang, Decision Theory for Discrimination-aware Classification. Retrieved 17 December 2019
 , the target variable, from known characteristics
, the target variable, from known characteristics  . We model
. We model  as a discrete
as a discrete  the prediction of the
the prediction of the  satisfy independence if the sensitive characteristics
satisfy independence if the sensitive characteristics  We can also express this notion with the following formula:
We can also express this notion with the following formula:
 This means that the classification rate for each target classes is equal for people belonging to different groups with respect to sensitive characteristics
This means that the classification rate for each target classes is equal for people belonging to different groups with respect to sensitive characteristics  .
.
 In this formula,
In this formula,  is the
is the  . Then
. Then  .
.
 and is given by the formula:
and is given by the formula:

 .
.
 satisfy separation if the sensitive characteristics
satisfy separation if the sensitive characteristics  We can also express this notion with the following formula:
We can also express this notion with the following formula:
 This means that all the dependence of the decision
This means that all the dependence of the decision  on the sensitive attribute
on the sensitive attribute  .
.


 We can also express this notion with the following formula:
We can also express this notion with the following formula:
 This means that the
This means that the 







 refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class.
refers to the score given by the classifier, which is the probability of a certain subject to be in the positive or the negative class. 















 ).
). and recall
and recall  ).
). and negative predictive value
and negative predictive value  ).
).
 and other features
and other features  and the same individual if she had
and the same individual if she had  , they should have same chance of being accepted.
The symbol
, they should have same chance of being accepted.
The symbol  represents the counterfactual random variable
represents the counterfactual random variable  means that this requirement is at the individual level, in that we are conditioning on all the variables identifying a single observation.
means that this requirement is at the individual level, in that we are conditioning on all the variables identifying a single observation.

 denotes the outcome given that the decision
denotes the outcome given that the decision  was taken, and
was taken, and  ) between
) between  ), representing possible spurious (i.e., non causal) effects of the sensitive attributes on the outcome.
), representing possible spurious (i.e., non causal) effects of the sensitive attributes on the outcome. with respect to the group
with respect to the group  can be defined as follows:
can be defined as follows:

 and equal to
and equal to 

 we get:
we get:

 we compute the weighted discrimination with respect to group
we compute the weighted discrimination with respect to group 
 to minimize some
to minimize some  . The second one, the adversary tries to accomplish the task of predicting
. The second one, the adversary tries to accomplish the task of predicting  by modifying its weights
by modifying its weights  to minimize some loss function
to minimize some loss function  .
An important point here is that, to propagate correctly,
.
An important point here is that, to propagate correctly,  at each training step according to the
at each training step according to the  and we modify
and we modify  where
where  is a tunable
is a tunable  (therefore the term
(therefore the term  ) while, at the same time, maximize
) while, at the same time, maximize  ), so that the adversary fails at predicting the sensitive variable from
), so that the adversary fails at predicting the sensitive variable from  prevents the predictor from moving in a direction that helps the adversary decrease its loss function.
prevents the predictor from moving in a direction that helps the adversary decrease its loss function.
 be the probability computed by the classifiers as the
be the probability computed by the classifiers as the  with a certain
with a certain  such that
such that  .
.
 ) then label it as positive, otherwise, label it as negative.
) then label it as positive, otherwise, label it as negative.