| Hoffman graph | |
|---|---|
 The Hoffman graph The Hoffman graph | |
| Named after | Alan Hoffman |
| Vertices | 16 |
| Edges | 32 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 4 |
| Automorphisms | 48 (Z/2Z × S4) |
| Chromatic number | 2 |
| Chromatic index | 4 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Hamiltonian Bipartite Perfect Eulerian 1-walk regular |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Hoffman graph is a 4-regular graph with 16 vertices and 32 edges discovered by Alan Hoffman. Published in 1963, it is cospectral to the hypercube graph Q4.
The Hoffman graph has many common properties with the hypercube Q4—both are Hamiltonian and have chromatic number 2, chromatic index 4, girth 4 and diameter 4. It is also a 4-vertex-connected graph and a 4-edge-connected graph. However, it is not distance-regular. It has book thickness 3 and queue number 2.
Algebraic properties
The Hoffman graph is not a vertex-transitive graph and its full automorphism group is a group of order 48 isomorphic to the direct product of the symmetric group S4 and the cyclic group Z/2Z. Despite not being vertex- or edge-transitive, the Hoffmann graph is still 1-walk-regular (but not distance-regular).
The characteristic polynomial of the Hoffman graph is equal to
making it an integral graph—a graph whose spectrum consists entirely of integers. It is the same spectrum as the hypercube Q4.
Gallery
-
 The Hoffman graph is Hamiltonian.
The Hoffman graph is Hamiltonian.
-
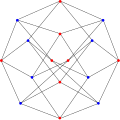 The chromatic number of the Hoffman graph is 2.
The chromatic number of the Hoffman graph is 2.
-
 The chromatic index of the Hoffman graph is 4.
The chromatic index of the Hoffman graph is 4.
References
- Weisstein, Eric W. "Hamiltonian Graph". MathWorld.
- Weisstein, Eric W. "Hoffman graph". MathWorld.
- Hoffman, A. J. "On the Polynomial of a Graph." Amer. Math. Monthly 70, 30-36, 1963.
- van Dam, E. R. and Haemers, W. H. "Spectral Characterizations of Some Distance-Regular Graphs." J. Algebraic Combin. 15, 189-202, 2003.
- Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
