| Part of a series on |
| Classical mechanics |
|---|
| Second law of motion |
| Branches |
| Fundamentals |
| Formulations |
| Core topics |
| Rotation |
| Scientists |
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative to the frame until acted upon by external forces. In such a frame, the laws of nature can be observed without the need to correct for acceleration.
All frames of reference with zero acceleration are in a state of constant rectilinear motion (straight-line motion) with respect to one another. In such a frame, an object with zero net force acting on it, is perceived to move with a constant velocity, or, equivalently, Newton's first law of motion holds. Such frames are known as inertial. Some physicists, like Isaac Newton, originally thought that one of these frames was absolute — the one approximated by the fixed stars. However, this is not required for the definition, and it is now known that those stars are in fact moving.
According to the principle of special relativity, all physical laws look the same in all inertial reference frames, and no inertial frame is privileged over another. Measurements of objects in one inertial frame can be converted to measurements in another by a simple transformation — the Galilean transformation in Newtonian physics or the Lorentz transformation (combined with a translation) in special relativity; these approximately match when the relative speed of the frames is low, but differ as it approaches the speed of light.
By contrast, a non-inertial reference frame has non-zero acceleration. In such a frame, the interactions between physical objects vary depending on the acceleration of that frame with respect to an inertial frame. Viewed from the perspective of classical mechanics and special relativity, the usual physical forces caused by the interaction of objects have to be supplemented by fictitious forces caused by inertia. Viewed from the perspective of general relativity theory, the fictitious (i.e. inertial) forces are attributed to geodesic motion in spacetime.
Due to Earth's rotation, its surface is not an inertial frame of reference. The Coriolis effect can deflect certain forms of motion as seen from Earth, and the centrifugal force will reduce the effective gravity at the equator. Nevertheless, for many applications the Earth is an adequate approximation of an inertial reference frame.
Introduction
The motion of a body can only be described relative to something else—other bodies, observers, or a set of spacetime coordinates. These are called frames of reference. According to the first postulate of special relativity, all physical laws take their simplest form in an inertial frame, and there exist multiple inertial frames interrelated by uniform translation:
Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.
— Albert Einstein: The foundation of the general theory of relativity, Section A, §1
This simplicity manifests itself in that inertial frames have self-contained physics without the need for external causes, while physics in non-inertial frames has external causes. The principle of simplicity can be used within Newtonian physics as well as in special relativity:
The laws of Newtonian mechanics do not always hold in their simplest form...If, for instance, an observer is placed on a disc rotating relative to the earth, he/she will sense a 'force' pushing him/her toward the periphery of the disc, which is not caused by any interaction with other bodies. Here, the acceleration is not the consequence of the usual force, but of the so-called inertial force. Newton's laws hold in their simplest form only in a family of reference frames, called inertial frames. This fact represents the essence of the Galilean principle of relativity:
— Milutin Blagojević: Gravitation and Gauge Symmetries, p. 4
The laws of mechanics have the same form in all inertial frames.
However, this definition of inertial frames is understood to apply in the Newtonian realm and ignores relativistic effects.
In practical terms, the equivalence of inertial reference frames means that scientists within a box moving with a constant absolute velocity cannot determine this velocity by any experiment. Otherwise, the differences would set up an absolute standard reference frame. According to this definition, supplemented with the constancy of the speed of light, inertial frames of reference transform among themselves according to the Poincaré group of symmetry transformations, of which the Lorentz transformations are a subgroup. In Newtonian mechanics, inertial frames of reference are related by the Galilean group of symmetries.
Newton's inertial frame of reference
Absolute space
Main article: Absolute space and timeNewton posited an absolute space considered well-approximated by a frame of reference stationary relative to the fixed stars. An inertial frame was then one in uniform translation relative to absolute space. However, some "relativists", even at the time of Newton, felt that absolute space was a defect of the formulation, and should be replaced.
The expression inertial frame of reference (German: Inertialsystem) was coined by Ludwig Lange in 1885, to replace Newton's definitions of "absolute space and time" with a more operational definition:
A reference frame in which a mass point thrown from the same point in three different (non co-planar) directions follows rectilinear paths each time it is thrown, is called an inertial frame.
The inadequacy of the notion of "absolute space" in Newtonian mechanics is spelled out by Blagojevich:
- The existence of absolute space contradicts the internal logic of classical mechanics since, according to the Galilean principle of relativity, none of the inertial frames can be singled out.
- Absolute space does not explain inertial forces since they are related to acceleration with respect to any one of the inertial frames.
- Absolute space acts on physical objects by inducing their resistance to acceleration but it cannot be acted upon.
— Milutin Blagojević: Gravitation and Gauge Symmetries, p. 5
The utility of operational definitions was carried much further in the special theory of relativity. Some historical background including Lange's definition is provided by DiSalle, who says in summary:
The original question, "relative to what frame of reference do the laws of motion hold?" is revealed to be wrongly posed. The laws of motion essentially determine a class of reference frames, and (in principle) a procedure for constructing them.
— Robert DiSalle Space and Time: Inertial Frames
Newtonian mechanics
Classical theories that use the Galilean transformation postulate the equivalence of all inertial reference frames. The Galilean transformation transforms coordinates from one inertial reference frame, , to another, , by simple addition or subtraction of coordinates:
where r0 and t0 represent shifts in the origin of space and time, and v is the relative velocity of the two inertial reference frames. Under Galilean transformations, the time t2 − t1 between two events is the same for all reference frames and the distance between two simultaneous events (or, equivalently, the length of any object, |r2 − r1|) is also the same.
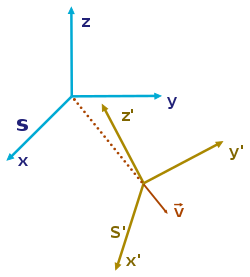
Within the realm of Newtonian mechanics, an inertial frame of reference, or inertial reference frame, is one in which Newton's first law of motion is valid. However, the principle of special relativity generalizes the notion of an inertial frame to include all physical laws, not simply Newton's first law.
Newton viewed the first law as valid in any reference frame that is in uniform motion (neither rotating nor accelerating) relative to absolute space; as a practical matter, "absolute space" was considered to be the fixed stars In the theory of relativity the notion of absolute space or a privileged frame is abandoned, and an inertial frame in the field of classical mechanics is defined as:
An inertial frame of reference is one in which the motion of a particle not subject to forces is in a straight line at constant speed.
Hence, with respect to an inertial frame, an object or body accelerates only when a physical force is applied, and (following Newton's first law of motion), in the absence of a net force, a body at rest will remain at rest and a body in motion will continue to move uniformly—that is, in a straight line and at constant speed. Newtonian inertial frames transform among each other according to the Galilean group of symmetries.
If this rule is interpreted as saying that straight-line motion is an indication of zero net force, the rule does not identify inertial reference frames because straight-line motion can be observed in a variety of frames. If the rule is interpreted as defining an inertial frame, then being able to determine when zero net force is applied is crucial. The problem was summarized by Einstein:
The weakness of the principle of inertia lies in this, that it involves an argument in a circle: a mass moves without acceleration if it is sufficiently far from other bodies; we know that it is sufficiently far from other bodies only by the fact that it moves without acceleration.
— Albert Einstein: The Meaning of Relativity, p. 58
There are several approaches to this issue. One approach is to argue that all real forces drop off with distance from their sources in a known manner, so it is only needed that a body is far enough away from all sources to ensure that no force is present. A possible issue with this approach is the historically long-lived view that the distant universe might affect matters (Mach's principle). Another approach is to identify all real sources for real forces and account for them. A possible issue with this approach is the possibility of missing something, or accounting inappropriately for their influence, perhaps, again, due to Mach's principle and an incomplete understanding of the universe. A third approach is to look at the way the forces transform when shifting reference frames. Fictitious forces, those that arise due to the acceleration of a frame, disappear in inertial frames and have complicated rules of transformation in general cases. Based on the universality of physical law and the request for frames where the laws are most simply expressed, inertial frames are distinguished by the absence of such fictitious forces.
Newton enunciated a principle of relativity himself in one of his corollaries to the laws of motion:
The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forward in a straight line.
— Isaac Newton: Principia, Corollary V, p. 88 in Andrew Motte translation
This principle differs from the special principle in two ways: first, it is restricted to mechanics, and second, it makes no mention of simplicity. It shares the special principle of the invariance of the form of the description among mutually translating reference frames. The role of fictitious forces in classifying reference frames is pursued further below.
Special relativity
Main article: Special relativityEinstein's theory of special relativity, like Newtonian mechanics, postulates the equivalence of all inertial reference frames. However, because special relativity postulates that the speed of light in free space is invariant, the transformation between inertial frames is the Lorentz transformation, not the Galilean transformation which is used in Newtonian mechanics.
The invariance of the speed of light leads to counter-intuitive phenomena, such as time dilation, length contraction, and the relativity of simultaneity. The predictions of special relativity have been extensively verified experimentally. The Lorentz transformation reduces to the Galilean transformation as the speed of light approaches infinity or as the relative velocity between frames approaches zero.
Examples
Simple example
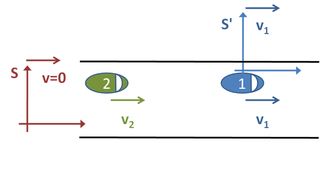
Consider a situation common in everyday life. Two cars travel along a road, both moving at constant velocities. See Figure 1. At some particular moment, they are separated by 200 meters. The car in front is traveling at 22 meters per second and the car behind is traveling at 30 meters per second. If we want to find out how long it will take the second car to catch up with the first, there are three obvious "frames of reference" that we could choose.
First, we could observe the two cars from the side of the road. We define our "frame of reference" S as follows. We stand on the side of the road and start a stop-clock at the exact moment that the second car passes us, which happens to be when they are a distance d = 200 m apart. Since neither of the cars is accelerating, we can determine their positions by the following formulas, where is the position in meters of car one after time t in seconds and is the position of car two after time t.
Notice that these formulas predict at t = 0 s the first car is 200m down the road and the second car is right beside us, as expected. We want to find the time at which . Therefore, we set and solve for , that is:
Alternatively, we could choose a frame of reference S′ situated in the first car. In this case, the first car is stationary and the second car is approaching from behind at a speed of v2 − v1 = 8 m/s. To catch up to the first car, it will take a time of d/v2 − v1 = 200/8 s, that is, 25 seconds, as before. Note how much easier the problem becomes by choosing a suitable frame of reference. The third possible frame of reference would be attached to the second car. That example resembles the case just discussed, except the second car is stationary and the first car moves backward towards it at 8 m/s.
It would have been possible to choose a rotating, accelerating frame of reference, moving in a complicated manner, but this would have served to complicate the problem unnecessarily. It is also necessary to note that one can convert measurements made in one coordinate system to another. For example, suppose that your watch is running five minutes fast compared to the local standard time. If you know that this is the case, when somebody asks you what time it is, you can deduct five minutes from the time displayed on your watch to obtain the correct time. The measurements that an observer makes about a system depend therefore on the observer's frame of reference (you might say that the bus arrived at 5 past three, when in fact it arrived at three).
Additional example
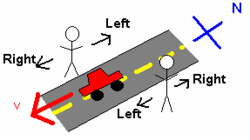
For a simple example involving only the orientation of two observers, consider two people standing, facing each other on either side of a north-south street. See Figure 2. A car drives past them heading south. For the person facing east, the car was moving to the right. However, for the person facing west, the car was moving to the left. This discrepancy is because the two people used two different frames of reference from which to investigate this system.
For a more complex example involving observers in relative motion, consider Alfred, who is standing on the side of a road watching a car drive past him from left to right. In his frame of reference, Alfred defines the spot where he is standing as the origin, the road as the x-axis, and the direction in front of him as the positive y-axis. To him, the car moves along the x axis with some velocity v in the positive x-direction. Alfred's frame of reference is considered an inertial frame because he is not accelerating, ignoring effects such as Earth's rotation and gravity.
Now consider Betsy, the person driving the car. Betsy, in choosing her frame of reference, defines her location as the origin, the direction to her right as the positive x-axis, and the direction in front of her as the positive y-axis. In this frame of reference, it is Betsy who is stationary and the world around her that is moving – for instance, as she drives past Alfred, she observes him moving with velocity v in the negative y-direction. If she is driving north, then north is the positive y-direction; if she turns east, east becomes the positive y-direction.
Finally, as an example of non-inertial observers, assume Candace is accelerating her car. As she passes by him, Alfred measures her acceleration and finds it to be a in the negative x-direction. Assuming Candace's acceleration is constant, what acceleration does Betsy measure? If Betsy's velocity v is constant, she is in an inertial frame of reference, and she will find the acceleration to be the same as Alfred in her frame of reference, a in the negative y-direction. However, if she is accelerating at rate A in the negative y-direction (in other words, slowing down), she will find Candace's acceleration to be a′ = a − A in the negative y-direction—a smaller value than Alfred has measured. Similarly, if she is accelerating at rate A in the positive y-direction (speeding up), she will observe Candace's acceleration as a′ = a + A in the negative y-direction—a larger value than Alfred's measurement.
Non-inertial frames
Main articles: Fictitious force, Non-inertial frame, and Rotating frame of referenceHere the relation between inertial and non-inertial observational frames of reference is considered. The basic difference between these frames is the need in non-inertial frames for fictitious forces, as described below.
General relativity
Main articles: General relativity and Introduction to general relativity See also: Equivalence principle and Eötvös experimentGeneral relativity is based upon the principle of equivalence:
There is no experiment observers can perform to distinguish whether an acceleration arises because of a gravitational force or because their reference frame is accelerating.
— Douglas C. Giancoli, Physics for Scientists and Engineers with Modern Physics, p. 155.
This idea was introduced in Einstein's 1907 article "Principle of Relativity and Gravitation" and later developed in 1911. Support for this principle is found in the Eötvös experiment, which determines whether the ratio of inertial to gravitational mass is the same for all bodies, regardless of size or composition. To date no difference has been found to a few parts in 10. For some discussion of the subtleties of the Eötvös experiment, such as the local mass distribution around the experimental site (including a quip about the mass of Eötvös himself), see Franklin.
Einstein's general theory modifies the distinction between nominally "inertial" and "non-inertial" effects by replacing special relativity's "flat" Minkowski Space with a metric that produces non-zero curvature. In general relativity, the principle of inertia is replaced with the principle of geodesic motion, whereby objects move in a way dictated by the curvature of spacetime. As a consequence of this curvature, it is not a given in general relativity that inertial objects moving at a particular rate with respect to each other will continue to do so. This phenomenon of geodesic deviation means that inertial frames of reference do not exist globally as they do in Newtonian mechanics and special relativity.
However, the general theory reduces to the special theory over sufficiently small regions of spacetime, where curvature effects become less important and the earlier inertial frame arguments can come back into play. Consequently, modern special relativity is now sometimes described as only a "local theory". "Local" can encompass, for example, the entire Milky Way galaxy: The astronomer Karl Schwarzschild observed the motion of pairs of stars orbiting each other. He found that the two orbits of the stars of such a system lie in a plane, and the perihelion of the orbits of the two stars remains pointing in the same direction with respect to the Solar System. Schwarzschild pointed out that that was invariably seen: the direction of the angular momentum of all observed double star systems remains fixed with respect to the direction of the angular momentum of the Solar System. These observations allowed him to conclude that inertial frames inside the galaxy do not rotate with respect to one another, and that the space of the Milky Way is approximately Galilean or Minkowskian.
Inertial frames and rotation
In an inertial frame, Newton's first law, the law of inertia, is satisfied: Any free motion has a constant magnitude and direction. Newton's second law for a particle takes the form:
with F the net force (a vector), m the mass of a particle and a the acceleration of the particle (also a vector) which would be measured by an observer at rest in the frame. The force F is the vector sum of all "real" forces on the particle, such as contact forces, electromagnetic, gravitational, and nuclear forces.
In contrast, Newton's second law in a rotating frame of reference (a non-inertial frame of reference), rotating at angular rate Ω about an axis, takes the form:
which looks the same as in an inertial frame, but now the force F′ is the resultant of not only F, but also additional terms (the paragraph following this equation presents the main points without detailed mathematics):
where the angular rotation of the frame is expressed by the vector Ω pointing in the direction of the axis of rotation, and with magnitude equal to the angular rate of rotation Ω, symbol × denotes the vector cross product, vector xB locates the body and vector vB is the velocity of the body according to a rotating observer (different from the velocity seen by the inertial observer).
The extra terms in the force F′ are the "fictitious" forces for this frame, whose causes are external to the system in the frame. The first extra term is the Coriolis force, the second the centrifugal force, and the third the Euler force. These terms all have these properties: they vanish when Ω = 0; that is, they are zero for an inertial frame (which, of course, does not rotate); they take on a different magnitude and direction in every rotating frame, depending upon its particular value of Ω; they are ubiquitous in the rotating frame (affect every particle, regardless of circumstance); and they have no apparent source in identifiable physical sources, in particular, matter. Also, fictitious forces do not drop off with distance (unlike, for example, nuclear forces or electrical forces). For example, the centrifugal force that appears to emanate from the axis of rotation in a rotating frame increases with distance from the axis.
All observers agree on the real forces, F; only non-inertial observers need fictitious forces. The laws of physics in the inertial frame are simpler because unnecessary forces are not present.
In Newton's time the fixed stars were invoked as a reference frame, supposedly at rest relative to absolute space. In reference frames that were either at rest with respect to the fixed stars or in uniform translation relative to these stars, Newton's laws of motion were supposed to hold. In contrast, in frames accelerating with respect to the fixed stars, an important case being frames rotating relative to the fixed stars, the laws of motion did not hold in their simplest form, but had to be supplemented by the addition of fictitious forces, for example, the Coriolis force and the centrifugal force. Two experiments were devised by Newton to demonstrate how these forces could be discovered, thereby revealing to an observer that they were not in an inertial frame: the example of the tension in the cord linking two spheres rotating about their center of gravity, and the example of the curvature of the surface of water in a rotating bucket. In both cases, application of Newton's second law would not work for the rotating observer without invoking centrifugal and Coriolis forces to account for their observations (tension in the case of the spheres; parabolic water surface in the case of the rotating bucket).
As now known, the fixed stars are not fixed. Those that reside in the Milky Way turn with the galaxy, exhibiting proper motions. Those that are outside our galaxy (such as nebulae once mistaken to be stars) participate in their own motion as well, partly due to expansion of the universe, and partly due to peculiar velocities. For instance, the Andromeda Galaxy is on collision course with the Milky Way at a speed of 117 km/s. The concept of inertial frames of reference is no longer tied to either the fixed stars or to absolute space. Rather, the identification of an inertial frame is based on the simplicity of the laws of physics in the frame. The laws of nature take a simpler form in inertial frames of reference because in these frames one did not have to introduce inertial forces when writing down Newton's law of motion.
In practice, using a frame of reference based upon the fixed stars as though it were an inertial frame of reference introduces little discrepancy. For example, the centrifugal acceleration of the Earth because of its rotation about the Sun is about thirty million times greater than that of the Sun about the galactic center.
To illustrate further, consider the question: "Does the Universe rotate?" An answer might explain the shape of the Milky Way galaxy using the laws of physics, although other observations might be more definitive; that is, provide larger discrepancies or less measurement uncertainty, like the anisotropy of the microwave background radiation or Big Bang nucleosynthesis. The flatness of the Milky Way depends on its rate of rotation in an inertial frame of reference. If its apparent rate of rotation is attributed entirely to rotation in an inertial frame, a different "flatness" is predicted than if it is supposed that part of this rotation is actually due to rotation of the universe and should not be included in the rotation of the galaxy itself. Based upon the laws of physics, a model is set up in which one parameter is the rate of rotation of the Universe. If the laws of physics agree more accurately with observations in a model with rotation than without it, we are inclined to select the best-fit value for rotation, subject to all other pertinent experimental observations. If no value of the rotation parameter is successful and theory is not within observational error, a modification of physical law is considered, for example, dark matter is invoked to explain the galactic rotation curve. So far, observations show any rotation of the universe is very slow, no faster than once every 6×10 years (10 rad/yr), and debate persists over whether there is any rotation. However, if rotation were found, interpretation of observations in a frame tied to the universe would have to be corrected for the fictitious forces inherent in such rotation in classical physics and special relativity, or interpreted as the curvature of spacetime and the motion of matter along the geodesics in general relativity.
When quantum effects are important, there are additional conceptual complications that arise in quantum reference frames.
Primed frames
An accelerated frame of reference is often delineated as being the "primed" frame, and all variables that are dependent on that frame are notated with primes, e.g. x′, y′, a′.
The vector from the origin of an inertial reference frame to the origin of an accelerated reference frame is commonly notated as R. Given a point of interest that exists in both frames, the vector from the inertial origin to the point is called r, and the vector from the accelerated origin to the point is called r′.
From the geometry of the situation
Taking the first and second derivatives of this with respect to time
where V and A are the velocity and acceleration of the accelerated system with respect to the inertial system and v and a are the velocity and acceleration of the point of interest with respect to the inertial frame.
These equations allow transformations between the two coordinate systems; for example, Newton's second law can be written as
When there is accelerated motion due to a force being exerted there is manifestation of inertia. If an electric car designed to recharge its battery system when decelerating is switched to braking, the batteries are recharged, illustrating the physical strength of manifestation of inertia. However, the manifestation of inertia does not prevent acceleration (or deceleration), for manifestation of inertia occurs in response to change in velocity due to a force. Seen from the perspective of a rotating frame of reference the manifestation of inertia appears to exert a force (either in centrifugal direction, or in a direction orthogonal to an object's motion, the Coriolis effect).
A common sort of accelerated reference frame is a frame that is both rotating and translating (an example is a frame of reference attached to a CD which is playing while the player is carried).
This arrangement leads to the equation (see Fictitious force for a derivation):
or, to solve for the acceleration in the accelerated frame,
Multiplying through by the mass m gives
where
- (Euler force),
- (Coriolis force),
- (centrifugal force).
Separating non-inertial from inertial reference frames
Theory
Main article: Fictitious force See also: Non-inertial frame, Rotating spheres, and Bucket argument

Inertial and non-inertial reference frames can be distinguished by the absence or presence of fictitious forces.
The effect of this being in the noninertial frame is to require the observer to introduce a fictitious force into his calculations…
— Sidney Borowitz and Lawrence A Bornstein in A Contemporary View of Elementary Physics, p. 138
The presence of fictitious forces indicates the physical laws are not the simplest laws available, in terms of the special principle of relativity, a frame where fictitious forces are present is not an inertial frame:
The equations of motion in a non-inertial system differ from the equations in an inertial system by additional terms called inertial forces. This allows us to detect experimentally the non-inertial nature of a system.
— V. I. Arnol'd: Mathematical Methods of Classical Mechanics Second Edition, p. 129
Bodies in non-inertial reference frames are subject to so-called fictitious forces (pseudo-forces); that is, forces that result from the acceleration of the reference frame itself and not from any physical force acting on the body. Examples of fictitious forces are the centrifugal force and the Coriolis force in rotating reference frames.
To apply the Newtonian definition of an inertial frame, the understanding of separation between "fictitious" forces and "real" forces must be made clear.
For example, consider a stationary object in an inertial frame. Being at rest, no net force is applied. But in a frame rotating about a fixed axis, the object appears to move in a circle, and is subject to centripetal force. How can it be decided that the rotating frame is a non-inertial frame? There are two approaches to this resolution: one approach is to look for the origin of the fictitious forces (the Coriolis force and the centrifugal force). It will be found there are no sources for these forces, no associated force carriers, no originating bodies. A second approach is to look at a variety of frames of reference. For any inertial frame, the Coriolis force and the centrifugal force disappear, so application of the principle of special relativity would identify these frames where the forces disappear as sharing the same and the simplest physical laws, and hence rule that the rotating frame is not an inertial frame.
Newton examined this problem himself using rotating spheres, as shown in Figure 2 and Figure 3. He pointed out that if the spheres are not rotating, the tension in the tying string is measured as zero in every frame of reference. If the spheres only appear to rotate (that is, we are watching stationary spheres from a rotating frame), the zero tension in the string is accounted for by observing that the centripetal force is supplied by the centrifugal and Coriolis forces in combination, so no tension is needed. If the spheres really are rotating, the tension observed is exactly the centripetal force required by the circular motion. Thus, measurement of the tension in the string identifies the inertial frame: it is the one where the tension in the string provides exactly the centripetal force demanded by the motion as it is observed in that frame, and not a different value. That is, the inertial frame is the one where the fictitious forces vanish.
For linear acceleration, Newton expressed the idea of undetectability of straight-line accelerations held in common:
If bodies, any how moved among themselves, are urged in the direction of parallel lines by equal accelerative forces, they will continue to move among themselves, after the same manner as if they had been urged by no such forces.
— Isaac Newton: Principia Corollary VI, p. 89, in Andrew Motte translation
This principle generalizes the notion of an inertial frame. For example, an observer confined in a free-falling lift will assert that he himself is a valid inertial frame, even if he is accelerating under gravity, so long as he has no knowledge about anything outside the lift. So, strictly speaking, inertial frame is a relative concept. With this in mind, inertial frames can collectively be defined as a set of frames which are stationary or moving at constant velocity with respect to each other, so that a single inertial frame is defined as an element of this set.
For these ideas to apply, everything observed in the frame has to be subject to a base-line, common acceleration shared by the frame itself. That situation would apply, for example, to the elevator example, where all objects are subject to the same gravitational acceleration, and the elevator itself accelerates at the same rate.
Applications
Inertial navigation systems used a cluster of gyroscopes and accelerometers to determine accelerations relative to inertial space. After a gyroscope is spun up in a particular orientation in inertial space, the law of conservation of angular momentum requires that it retain that orientation as long as no external forces are applied to it. Three orthogonal gyroscopes establish an inertial reference frame, and the accelerators measure acceleration relative to that frame. The accelerations, along with a clock, can then be used to calculate the change in position. Thus, inertial navigation is a form of dead reckoning that requires no external input, and therefore cannot be jammed by any external or internal signal source.
A gyrocompass, employed for navigation of seagoing vessels, finds the geometric north. It does so, not by sensing the Earth's magnetic field, but by using inertial space as its reference. The outer casing of the gyrocompass device is held in such a way that it remains aligned with the local plumb line. When the gyroscope wheel inside the gyrocompass device is spun up, the way the gyroscope wheel is suspended causes the gyroscope wheel to gradually align its spinning axis with the Earth's axis. Alignment with the Earth's axis is the only direction for which the gyroscope's spinning axis can be stationary with respect to the Earth and not be required to change direction with respect to inertial space. After being spun up, a gyrocompass can reach the direction of alignment with the Earth's axis in as little as a quarter of an hour.
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2013) (Learn how and when to remove this message) |
See also
- Absolute rotation
- Diffeomorphism
- Galilean invariance
- General covariance
- Local reference frame
- Lorentz covariance
- Newton's first law
- Quantum reference frame
References
- ^ Milton A. Rothman (1989). Discovering the Natural Laws: The Experimental Basis of Physics. Courier Dover Publications. p. 23-24. ISBN 0-486-26178-6.
reference laws of physics.
- ^ Sidney Borowitz; Lawrence A. Bornstein (1968). A Contemporary View of Elementary Physics. McGraw-Hill. p. 138. ASIN B000GQB02A.
- Einstein, A.; Lorentz, H. A.; Minkowski, H.; Weyl, H. (1952). The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity. Courier Dover Publications. p. 111. ISBN 0-486-60081-5.
- Ferraro, Rafael (2007), Einstein's Space-Time: An Introduction to Special and General Relativity, Springer Science & Business Media, pp. 209–210, Bibcode:2007esti.book.....F, ISBN 9780387699462, archived from the original on 7 March 2023, retrieved 2 November 2022
- Ernest Nagel (1979). The Structure of Science. Hackett Publishing. p. 212. ISBN 0-915144-71-9.
- Milutin Blagojević (2002). Gravitation and Gauge Symmetries. CRC Press. p. 4. ISBN 0-7503-0767-6.
- Albert Einstein (1920). Relativity: The Special and General Theory. H. Holt and Company. p. 17.
The Principle of Relativity.
- Richard Phillips Feynman (1998). Six not-so-easy pieces: Einstein's relativity, symmetry, and space-time. Basic Books. p. 73. ISBN 0-201-32842-9.
- Armin Wachter; Henning Hoeber (2006). Compendium of Theoretical Physics. Birkhäuser. p. 98. ISBN 0-387-25799-3.
- Ernst Mach (1915). The Science of Mechanics. The Open Court Publishing Co. p. 38.
rotating sphere Mach cord OR string OR rod.
- Lange, Ludwig (1885). "Über die wissenschaftliche Fassung des Galileischen Beharrungsgesetzes". Philosophische Studien. 2.
- Julian B. Barbour (2001). The Discovery of Dynamics (Reprint of 1989 Absolute or Relative Motion? ed.). Oxford University Press. pp. 645–646. ISBN 0-19-513202-5.
- L. Lange (1885) as quoted by Max von Laue in his book (1921) Die Relativitätstheorie, p. 34, and translated by Harald Iro (2002). A Modern Approach to Classical Mechanics. World Scientific. p. 169. ISBN 981-238-213-5.
- Milutin Blagojević (2002). Gravitation and Gauge Symmetries. CRC Press. p. 5. ISBN 0-7503-0767-6.
- NMJ Woodhouse (2003). Special relativity. London: Springer. p. 58. ISBN 1-85233-426-6.
- Robert DiSalle (Summer 2002). "Space and Time: Inertial Frames". In Edward N. Zalta (ed.). The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 7 January 2016. Retrieved 9 September 2008.
- C Møller (1976). The Theory of Relativity (Second ed.). Oxford UK: Oxford University Press. p. 1. ISBN 0-19-560539-X. OCLC 220221617.
- For a discussion of the role of fixed stars, see Henning Genz (2001). Nothingness: The Science of Empty Space. Da Capo Press. p. 150. ISBN 0-7382-0610-5.
- Robert Resnick; David Halliday; Kenneth S. Krane (2001). Physics (5th ed.). Wiley. Volume 1, Chapter 3. ISBN 0-471-32057-9.
physics resnick.
- RG Takwale (1980). Introduction to classical mechanics. New Delhi: Tata McGraw-Hill. p. 70. ISBN 0-07-096617-6.
- NMJ Woodhouse (2003). Special relativity. London/Berlin: Springer. p. 6. ISBN 1-85233-426-6.
- A Einstein (1950). The Meaning of Relativity. Princeton University Press. p. 58.
- William Geraint Vaughan Rosser (1991). Introductory Special Relativity. CRC Press. p. 3. ISBN 0-85066-838-7.
- Richard Phillips Feynman (1998). Six not-so-easy pieces: Einstein's relativity, symmetry, and space-time. Basic Books. p. 50. ISBN 0-201-32842-9.
- ^ See the Principia on line at Andrew Motte Translation
- However, in the Newtonian system the Galilean transformation connects these frames and in the special theory of relativity the Lorentz transformation connects them. The two transformations agree for speeds of translation much less than the speed of light.
- Skinner, Ray (2014). Relativity for Scientists and Engineers (reprinted ed.). Courier Corporation. p. 27. ISBN 978-0-486-79367-2. Extract of page 27
- LD Landau; LM Lifshitz (1975). The Classical Theory of Fields (4th Revised English ed.). Pergamon Press. pp. 273–274. ISBN 978-0-7506-2768-9.
- Susskind, Leonard; Art Friedman (2017). Special relativity and classical field theory: the theoretical minimum. New York: Hachette UK. Figure 2.1. ISBN 978-0-465-09334-2. OCLC 968771417.
- David Morin (2008). Introduction to Classical Mechanics. Cambridge University Press. p. 649. ISBN 978-0-521-87622-3.
acceleration azimuthal Morin.
- Douglas C. Giancoli (2007). Physics for Scientists and Engineers with Modern Physics. Pearson Prentice Hall. p. 155. ISBN 978-0-13-149508-1.
- A. Einstein, "On the influence of gravitation on the propagation of light Archived 24 December 2020 at the Wayback Machine", Annalen der Physik, vol. 35, (1911) : 898–908
- National Research Council (US) (1986). Physics Through the Nineteen Nineties: Overview. National Academies Press. p. 15. ISBN 0-309-03579-1.
- Allan Franklin (2007). No Easy Answers: Science and the Pursuit of Knowledge. University of Pittsburgh Press. p. 66. ISBN 978-0-8229-5968-7.
- Green, Herbert S. (2000). Information Theory and Quantum Physics: Physical Foundations for Understanding the Conscious Process. Springer. p. 154. ISBN 354066517X. Extract of page 154
- Bandyopadhyay, Nikhilendu (2000). Theory of Special Relativity. Academic Publishers. p. 116. ISBN 8186358528. Extract of page 116
- Liddle, Andrew R.; Lyth, David H. (2000). Cosmological Inflation and Large-Scale Structure. Cambridge University Press. p. 329. ISBN 0-521-57598-2. Extract of page 329
- In the Shadow of the Relativity Revolution Archived 20 May 2017 at the Wayback Machine Section 3: The Work of Karl Schwarzschild (2.2 MB PDF-file)
- Landau, L. D.; Lifshitz, E. M. (1960). Mechanics (PDF). Pergamon Press. pp. 4–6.
- Amedeo Balbi (2008). The Music of the Big Bang. Springer. p. 59. ISBN 978-3-540-78726-6.
- Abraham Loeb; Mark J. Reid; Andreas Brunthaler; Heino Falcke (2005). "Constraints on the proper motion of the Andromeda Galaxy based on the survival of its satellite M33" (PDF). The Astrophysical Journal. 633 (2): 894–898. arXiv:astro-ph/0506609. Bibcode:2005ApJ...633..894L. doi:10.1086/491644. S2CID 17099715. Archived (PDF) from the original on 11 August 2017. Retrieved 15 December 2008.
- John J. Stachel (2002). Einstein from "B" to "Z". Springer. pp. 235–236. ISBN 0-8176-4143-2.
- Peter Graneau; Neal Graneau (2006). In the Grip of the Distant Universe. World Scientific. p. 147. ISBN 981-256-754-2.
- Henning Genz (2001). Nothingness. Da Capo Press. p. 275. ISBN 0-7382-0610-5.
- J Garcio-Bellido (2005). "The Paradigm of Inflation". In J. M. T. Thompson (ed.). Advances in Astronomy. Imperial College Press. p. 32, §9. ISBN 1-86094-577-5.
- Wlodzimierz Godlowski; Marek Szydlowski (2003). "Dark energy and global rotation of the Universe". General Relativity and Gravitation. 35 (12): 2171–2187. arXiv:astro-ph/0303248. Bibcode:2003GReGr..35.2171G. doi:10.1023/A:1027301723533. S2CID 118988129.
- Birch, P. (29 July 1982). "Is the Universe rotating?". Nature. 298 (5873): 451–454. Bibcode:1982Natur.298..451B. doi:10.1038/298451a0. S2CID 4343095. Archived from the original on 5 March 2016. Retrieved 14 December 2008.
- Gilson, James G. (1 September 2004), Mach's Principle II, arXiv:physics/0409010, Bibcode:2004physics...9010G
- V. I. Arnol'd (1989). Mathematical Methods of Classical Mechanics. Springer. p. 129. ISBN 978-0-387-96890-2.
- For example, there is no body providing a gravitational or electrical attraction.
- That is, the universality of the laws of physics requires the same tension to be seen by everybody. For example, it cannot happen that the string breaks under extreme tension in one frame of reference and remains intact in another frame of reference, just because we choose to look at the string from a different frame.
- Chatfield, Averil B. (1997). Fundamentals of High Accuracy Inertial Navigation, Volume 174. AIAA. ISBN 9781600864278.
- Kennie, T.J.M.; Petrie, G., eds. (1993). Engineering Surveying Technology (pbk. ed.). Hoboken: Taylor & Francis. p. 95. ISBN 9780203860748.
- "The gyroscope pilots ships & planes". Life. 15 March 1943. pp. 80–83.
Further reading
- Edwin F. Taylor and John Archibald Wheeler, Spacetime Physics, 2nd ed. (Freeman, NY, 1992)
- Albert Einstein, Relativity, the special and the general theories, 15th ed. (1954)
- Poincaré, Henri (1900). "La théorie de Lorentz et le Principe de Réaction". Archives Neerlandaises. V: 253–78.
- Albert Einstein, On the Electrodynamics of Moving Bodies, included in The Principle of Relativity, page 38. Dover 1923
- Rotation of the Universe
- Julian B. Barbour; Herbert Pfister (1998). Mach's Principle: From Newton's Bucket to Quantum Gravity. Birkhäuser. p. 445. ISBN 0-8176-3823-7.
- PJ Nahin (1999). Time Machines. Springer. p. 369; Footnote 12. ISBN 0-387-98571-9.
- B Ciobanu, I Radinchi Archived 19 July 2013 at the Wayback Machine Modeling the electric and magnetic fields in a rotating universe Rom. Journ. Phys., Vol. 53, Nos. 1–2, P. 405–415, Bucharest, 2008
- Yuri N. Obukhov, Thoralf Chrobok, Mike Scherfner Archived 9 July 2017 at the Wayback Machine Shear-free rotating inflation Phys. Rev. D 66, 043518 (2002)
- Yuri N. Obukhov On physical foundations and observational effects of cosmic rotation (2000)
- Li-Xin Li Archived 9 July 2017 at the Wayback Machine Effect of the Global Rotation of the Universe on the Formation of Galaxies General Relativity and Gravitation, 30 (1998) doi:10.1023/A:1018867011142
- P Birch Archived 5 March 2016 at the Wayback Machine Is the Universe rotating? Nature 298, 451 – 454 (29 July 1982)
- Kurt Gödel An example of a new type of cosmological solutions of Einstein's field equations of gravitation Rev. Mod. Phys., Vol. 21, p. 447, 1949.
External links
- Stanford Encyclopedia of Philosophy entry Archived 4 December 2010 at the Wayback Machine
- Animation clip on YouTube showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
- "Is Gravity An Illusion?". PBS Space Time. 3 June 2015. Archived from the original on 13 November 2021 – via YouTube.

 , to another,
, to another,  , by simple addition or subtraction of coordinates:
, by simple addition or subtraction of coordinates:


 . Frame S' has an arbitrary but fixed rotation with respect to frame S. They are both inertial frames provided a body not subject to forces appears to move in a straight line. If that motion is seen in one frame, it will also appear that way in the other.
. Frame S' has an arbitrary but fixed rotation with respect to frame S. They are both inertial frames provided a body not subject to forces appears to move in a straight line. If that motion is seen in one frame, it will also appear that way in the other. is the position in meters of car one after time t in seconds and
is the position in meters of car one after time t in seconds and  is the position of car two after time t.
is the position of car two after time t.

 . Therefore, we set
. Therefore, we set  , that is:
, that is:













 (
( (
( (
(