| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Infinite dihedral group" – news · newspapers · books · scholar · JSTOR (July 2011) (Learn how and when to remove this message) |
| p1m1, (*∞∞) | p2, (22∞) | p2mg, (2*∞) |
|---|---|---|
|

|

|
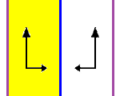
| In 2-dimensions three frieze groups p1m1, p2, and p2mg are isomorphic to the Dih∞ group. They all have 2 generators. The first has two parallel reflection lines, the second two 2-fold gyrations, and the last has one mirror and one 2-fold gyration. | ||

In mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.
In two-dimensional geometry, the infinite dihedral group represents the frieze group symmetry, p1m1, seen as an infinite set of parallel reflections along an axis.
Definition
Every dihedral group is generated by a rotation r and a reflection; if the rotation is a rational multiple of a full rotation, then there is some integer n such that r is the identity, and we have a finite dihedral group of order 2n. If the rotation is not a rational multiple of a full rotation, then there is no such n and the resulting group has infinitely many elements and is called Dih∞. It has presentations
and is isomorphic to a semidirect product of Z and Z/2, and to the free product Z/2 * Z/2. It is the automorphism group of the graph consisting of a path infinite to both sides. Correspondingly, it is the isometry group of Z (see also symmetry groups in one dimension), the group of permutations α: Z → Z satisfying |i − j| = |α(i) − α(j)|, for all i, j in Z.
The infinite dihedral group can also be defined as the holomorph of the infinite cyclic group.
Aliasing

An example of infinite dihedral symmetry is in aliasing of real-valued signals.
When sampling a function at frequency fs (intervals 1/fs), the following functions yield identical sets of samples: {sin(2π( f + Nfs) t + φ), N = 0, ±1, ±2, ±3, . . . }. Thus, the detected value of frequency f is periodic, which gives the translation element r = fs. The functions and their frequencies are said to be aliases of each other. Noting the trigonometric identity:
we can write all the alias frequencies as positive values: . This gives the reflection (f) element, namely f ↦ −f. For example, with f = 0.6fs and N = −1, f + Nfs = −0.4fs reflects to 0.4fs, resulting in the two left-most black dots in the figure. The other two dots correspond to N = −2 and N = 1. As the figure depicts, there are reflection symmetries, at 0.5fs, fs, 1.5fs, etc. Formally, the quotient under aliasing is the orbifold , with a Z/2 action at the endpoints (the orbifold points), corresponding to reflection.
See also
- The orthogonal group O(2), another infinite generalization of the finite dihedral groups
- The affine symmetric group, a family of groups including the infinite dihedral group
Notes
- In signal processing, the symmetry about axis fs/2 is known as folding, and the axis is known as the folding frequency.
References
- Connolly, Francis; Davis, James (August 2004). "The surgery obstruction groups of the infinite dihedral group". Geometry & Topology. 8 (3): 1043–1078. arXiv:math/0306054. doi:10.2140/gt.2004.8.1043.
- Meenaxi Bhattacharjee, Dugald Macpherson, Rögnvaldur G. Möller, Peter M. Neumann. Notes on Infinite Permutation Groups, Issue 1689. Springer, 1998. p. 38. ISBN 978-3-540-64965-6



 . This gives the reflection (f) element, namely f ↦ −f. For example, with f = 0.6fs and N = −1, f + Nfs = −0.4fs reflects to 0.4fs, resulting in the two left-most black dots in the figure. The other two dots correspond to N = −2 and N = 1. As the figure depicts, there are reflection symmetries, at 0.5fs, fs, 1.5fs, etc. Formally, the quotient under aliasing is the
. This gives the reflection (f) element, namely f ↦ −f. For example, with f = 0.6fs and N = −1, f + Nfs = −0.4fs reflects to 0.4fs, resulting in the two left-most black dots in the figure. The other two dots correspond to N = −2 and N = 1. As the figure depicts, there are reflection symmetries, at 0.5fs, fs, 1.5fs, etc. Formally, the quotient under aliasing is the