| This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Infinite impulse response" – news · newspapers · books · scholar · JSTOR (April 2015) (Learn how and when to remove this message) |
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response does become exactly zero at times for some finite , thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as IIR systems or IIR filters.
In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filters. On the other hand, discrete-time filters (usually digital filters) based on a tapped delay line employing no feedback are necessarily FIR filters. The capacitors (or inductors) in the analog filter have a "memory" and their internal state never completely relaxes following an impulse (assuming the classical model of capacitors and inductors where quantum effects are ignored). But in the latter case, after an impulse has reached the end of the tapped delay line, the system has no further memory of that impulse and has returned to its initial state; its impulse response beyond that point is exactly zero.
Implementation and design
Although almost all analog electronic filters are IIR, digital filters may be either IIR or FIR. The presence of feedback in the topology of a discrete-time filter (such as the block diagram shown below) generally creates an IIR response. The z domain transfer function of an IIR filter contains a non-trivial denominator, describing those feedback terms. The transfer function of an FIR filter, on the other hand, has only a numerator as expressed in the general form derived below. All of the coefficients with (feedback terms) are zero and the filter has no finite poles.
The transfer functions pertaining to IIR analog electronic filters have been extensively studied and optimized for their amplitude and phase characteristics. These continuous-time filter functions are described in the Laplace domain. Desired solutions can be transferred to the case of discrete-time filters whose transfer functions are expressed in the z domain, through the use of certain mathematical techniques such as the bilinear transform, impulse invariance, or pole–zero matching method. Thus digital IIR filters can be based on well-known solutions for analog filters such as the Chebyshev filter, Butterworth filter, and elliptic filter, inheriting the characteristics of those solutions.
Transfer function derivation
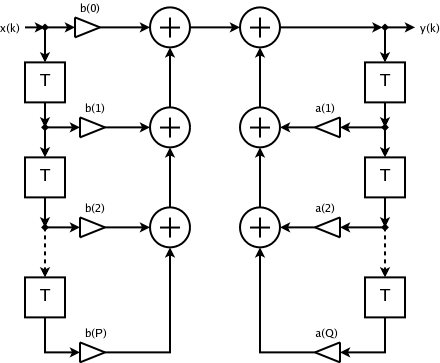
Digital filters are often described and implemented in terms of the difference equation that defines how the output signal is related to the input signal:
where:
- is the feedforward filter order
- are the feedforward filter coefficients
- is the feedback filter order
- are the feedback filter coefficients
- is the input signal
- is the output signal.
A more condensed form of the difference equation is:
To find the transfer function of the filter, we first take the Z-transform of each side of the above equation to obtain:
After rearranging:
We then define the transfer function to be:
Stability
The transfer function allows one to judge whether or not a system is bounded-input, bounded-output (BIBO) stable. To be specific, the BIBO stability criterion requires that the ROC of the system includes the unit circle. For example, for a causal system, all poles of the transfer function have to have an absolute value smaller than one. In other words, all poles must be located within a unit circle in the -plane.
The poles are defined as the values of which make the denominator of equal to 0:
Clearly, if then the poles are not located at the origin of the -plane. This is in contrast to the FIR filter where all poles are located at the origin, and is therefore always stable.
IIR filters are sometimes preferred over FIR filters because an IIR filter can achieve a much sharper transition region roll-off than an FIR filter of the same order.
Example
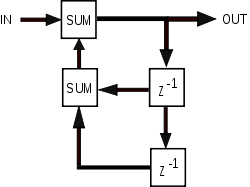
Let the transfer function of a discrete-time filter be given by:
governed by the parameter , a real number with . is stable and causal with a pole at . The time-domain impulse response can be shown to be given by:
where is the unit step function. It can be seen that is non-zero for all , thus an impulse response which continues infinitely.
Advantages and disadvantages
The main advantage digital IIR filters have over FIR filters is their efficiency in implementation, in order to meet a specification in terms of passband, stopband, ripple, and/or roll-off. Such a set of specifications can be accomplished with a lower order (Q in the above formulae) IIR filter than would be required for an FIR filter meeting the same requirements. If implemented in a signal processor, this implies a correspondingly fewer number of calculations per time step; the computational savings is often of a rather large factor.
On the other hand, FIR filters can be easier to design, for instance, to match a particular frequency response requirement. This is particularly true when the requirement is not one of the usual cases (high-pass, low-pass, notch, etc.) which have been studied and optimized for analog filters. Also FIR filters can be easily made to be linear phase (constant group delay vs frequency)—a property that is not easily met using IIR filters and then only as an approximation (for instance with the Bessel filter). Another issue regarding digital IIR filters is the potential for limit cycle behavior when idle, due to the feedback system in conjunction with quantization.
Design Methods
Impulse Invariance
Impulse invariance is a technique for designing discrete-time infinite-impulse-response (IIR) filters from continuous-time filters in which the impulse response of the continuous-time system is sampled to produce the impulse response of the discrete-time system.
Impulse invariance is one of the commonly used methods to meet the two basic requirements of the mapping from the s-plane to the z-plane. This is obtained by solving the T(z) that has the same output value at the same sampling time as the analog filter, and it is only applicable when the inputs are in a pulse.
Note that all inputs of the digital filter generated by this method are approximate values, except for pulse inputs that are very accurate. This is the simplest IIR filter design method. It is the most accurate at low frequencies, so it is usually used in low-pass filters.
For Laplace transform or z-transform, the output after the transformation is just the input multiplied by the corresponding transformation function, T(s) or T(z). Y(s) and Y(z) are the converted output of input X(s) and input X(z), respectively.
When applying the Laplace transform or z-transform on the unit impulse, the result is 1. Hence, the output results after the conversion are
Now the output of the analog filter is just the inverse Laplace transform in the time domain.
If we use nT instead of t, we can get the output y(nT) derived from the pulse at the sampling time. It can also be expressed as y(n)
This discrete time signal can be applied z-transform to get T(z)
The last equation mathematically describes that a digital IIR filter is to perform z-transform on the analog signal that has been sampled and converted to T(s) by Laplace, which is usually simplified to
Pay attention to the fact that there is a multiplier T appearing in the formula. This is because even if the Laplace transform and z-transform for the unit pulse are 1, the pulse itself is not necessarily the same. For analog signals, the pulse has an infinite value but the area is 1 at t=0, but it is 1 at the discrete-time pulse t=0, so the existence of a multiplier T is required.
Step Invariance
Step invariance is a better design method than impulse invariant. The digital filter has several segments of input with different constants when sampling, which is composed of discrete steps. The step invariant IIR filter is less accurate than the same input step signal to the ADC. However, it is a better approximation for any input than the impulse invariant.
Step invariant solves the problem of the same sample values when T(z) and T(s) are both step inputs. The input to the digital filter is u(n), and the input to the analog filter is u(t). Apply z-transform and Laplace transform on these two inputs to obtain the converted output signal.
Perform z-transform on step input
Converted output after z-transform
Perform Laplace transform on step input
Converted output after Laplace transform
The output of the analog filter is y(t), which is the inverse Laplace transform of Y(s). If sampled every T seconds, it is y(n), which is the inverse conversion of Y(z).These signals are used to solve for the digital filter and the analog filter and have the same output at the sampling time.
The following equation points out the solution of T(z), which is the approximate formula for the analog filter.
Bilinear Transform
The bilinear transform is a special case of a conformal mapping, often used to convert a transfer function of a linear, time-invariant (LTI) filter in the continuous-time domain (often called an analog filter) to a transfer function of a linear, shift-invariant filter in the discrete-time domain. The bilinear transform is a first-order approximation of the natural logarithm function that is an exact mapping of the z-plane to the s-plane. When the Laplace transform is performed on a discrete-time signal (with each element of the discrete-time sequence attached to a correspondingly delayed unit impulse), the result is precisely the Z transform of the discrete-time sequence with the substitution of
where is the numerical integration step size of the trapezoidal rule used in the bilinear transform derivation; or, in other words, the sampling period. The above bilinear approximation can be solved for or a similar approximation for can be performed.
The inverse of this mapping (and its first-order bilinear approximation) is
This relationship is used in the Laplace transfer function of any analog filter or the digital infinite impulse response (IIR) filter T(z) of the analog filter.
The bilinear transform essentially uses this first order approximation and substitutes into the continuous-time transfer function,
That is
which is used to calculate the IIR digital filter, starting from the Laplace transfer function of the analog filter.
See also
- Autoregressive model
- Electronic filter
- Finite impulse response
- Recurrence relation, mathematical formalization
- System analysis
External links
- The fifth module of the BORES Signal Processing DSP course - Introduction to DSP] at the Wayback Machine (archived July 2, 2016)
- IIR Digital Filter Design Applet at the Wayback Machine (archived February 13, 2010)
- IIR Digital Filter design tool Archived 2020-08-30 at the Wayback Machine - produces coefficients, graphs, poles, zeros, and C code
- EngineerJS Online IIR Design Tool - does not require Java
 that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a
that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a  for some finite
for some finite  , thus being of finite duration. Common examples of linear time-invariant systems are most
, thus being of finite duration. Common examples of linear time-invariant systems are most  coefficients with
coefficients with  (feedback terms) are zero and the filter has no finite
(feedback terms) are zero and the filter has no finite 
 is the feedforward filter order
is the feedforward filter order are the feedforward filter coefficients
are the feedforward filter coefficients is the feedback filter order
is the feedback filter order are the feedback filter coefficients
are the feedback filter coefficients is the input signal
is the input signal is the output signal.
is the output signal.



 block is a unit delay.
block is a unit delay. -plane.
-plane.
 equal to 0:
equal to 0:

 then the poles are not located at the origin of the
then the poles are not located at the origin of the 
 , a real number with
, a real number with  .
. 
 is the
is the  is non-zero for all
is non-zero for all  , thus an impulse response which continues infinitely.
, thus an impulse response which continues infinitely.


















 of a linear, time-invariant (LTI) filter in the continuous-time domain (often called an analog filter) to a transfer function
of a linear, time-invariant (LTI) filter in the continuous-time domain (often called an analog filter) to a transfer function  of a linear, shift-invariant filter in the discrete-time domain.
The bilinear transform is a first-order approximation of the natural logarithm function that is an exact mapping of the z-plane to the s-plane. When the Laplace transform is performed on a discrete-time signal (with each element of the discrete-time sequence attached to a correspondingly delayed unit impulse), the result is precisely the Z transform of the discrete-time sequence with the substitution of
of a linear, shift-invariant filter in the discrete-time domain.
The bilinear transform is a first-order approximation of the natural logarithm function that is an exact mapping of the z-plane to the s-plane. When the Laplace transform is performed on a discrete-time signal (with each element of the discrete-time sequence attached to a correspondingly delayed unit impulse), the result is precisely the Z transform of the discrete-time sequence with the substitution of

 or a similar approximation for
or a similar approximation for  can be performed.
can be performed.


