Ratio of the perimeter of Bernoulli's lemniscate to its diameter
"Gauss's constant" redirects here. For the parameter used in orbital mechanics, see Gaussian gravitational constant .
Lemniscate of Bernoulli In mathematics , the lemniscate constant ϖ is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter , analogous to the definition of π for the circle. Equivalently, the perimeter of the lemniscate
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle (x^{2}+y^{2})^{2}=x^{2}-y^{2}}
ϖ . The lemniscate constant is closely related to the lemniscate elliptic functions and approximately equal to 2.62205755. It also appears in evaluation of the gamma and beta function at certain rational values. The symbol ϖ is a cursive variant of π known as variant pi represented in Unicode by the character U+03D6 ϖ GREEK PI SYMBOL.
Sometimes the quantities 2ϖ or ϖ/2 are referred to as the lemniscate constant.
As of 2024 over 1.2 trillion digits of this constant have been calculated.
History
Gauss's constant , denoted by G , is equal to ϖ /π ≈ 0.8346268 and named after Carl Friedrich Gauss , who calculated it via the arithmetic–geometric mean as
1
/
M
(
1
,
2
)
{\displaystyle 1/M{\bigl (}1,{\sqrt {2}}{\bigr )}}
M
(
1
,
2
)
=
π
/
ϖ
{\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}=\pi /\varpi }
ϖ
{\displaystyle \varpi }
John Todd named two more lemniscate constants, the first lemniscate constant A = ϖ /2 ≈ 1.3110287771 and the second lemniscate constant B = π/(2ϖ ) ≈ 0.5990701173.
The lemniscate constant
ϖ
{\displaystyle \varpi }
A
{\displaystyle A}
transcendental by Carl Ludwig Siegel in 1932 and later by Theodor Schneider in 1937 and Todd's second lemniscate constant
B
{\displaystyle B}
G
{\displaystyle G}
Gregory Chudnovsky proved that the set
{
π
,
ϖ
}
{\displaystyle \{\pi ,\varpi \}}
algebraically independent over
Q
{\displaystyle \mathbb {Q} }
A
{\displaystyle A}
B
{\displaystyle B}
{
π
,
M
(
1
,
1
/
2
)
,
M
′
(
1
,
1
/
2
)
}
{\displaystyle {\bigl \{}\pi ,M{\bigl (}1,1/{\sqrt {2}}{\bigr )},M'{\bigl (}1,1/{\sqrt {2}}{\bigr )}{\bigr \}}}
derivative with respect to the second variable) is not algebraically independent over
Q
{\displaystyle \mathbb {Q} }
Yuri Nesterenko proved that the set
{
π
,
ϖ
,
e
π
}
{\displaystyle \{\pi ,\varpi ,e^{\pi }\}}
Q
{\displaystyle \mathbb {Q} }
Forms
Usually,
ϖ
{\displaystyle \varpi }
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2
∫
0
∞
d
t
1
+
t
4
=
∫
0
1
d
t
t
−
t
3
=
∫
1
∞
d
t
t
3
−
t
=
4
∫
0
∞
(
1
+
t
4
4
−
t
)
d
t
=
2
2
∫
0
1
1
−
t
4
4
d
t
=
3
∫
0
1
1
−
t
4
d
t
=
2
K
(
i
)
=
1
2
B
(
1
4
,
1
2
)
=
1
2
2
B
(
1
4
,
1
4
)
=
Γ
(
1
/
4
)
2
2
2
π
=
2
−
2
4
ζ
(
3
/
4
)
2
ζ
(
1
/
4
)
2
=
2.62205
75542
92119
81046
48395
89891
11941
…
,
{\displaystyle {\begin{aligned}\varpi &=2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\sqrt {2}}\int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {t-t^{3}}}}=\int _{1}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{3}-t}}}\\&=4\int _{0}^{\infty }{\Bigl (}{\sqrt{1+t^{4}}}-t{\Bigr )}\,\mathrm {d} t=2{\sqrt {2}}\int _{0}^{1}{\sqrt{1-t^{4}}}\mathop {\mathrm {d} t} =3\int _{0}^{1}{\sqrt {1-t^{4}}}\,\mathrm {d} t\\&=2K(i)={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}={\tfrac {1}{2{\sqrt {2}}}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\Gamma (1/4)^{2}}{2{\sqrt {2\pi }}}}={\frac {2-{\sqrt {2}}}{4}}{\frac {\zeta (3/4)^{2}}{\zeta (1/4)^{2}}}\\&=2.62205\;75542\;92119\;81046\;48395\;89891\;11941\ldots ,\end{aligned}}}
where K is the complete elliptic integral of the first kind with modulus k, Β is the beta function , Γ is the gamma function and ζ is the Riemann zeta function .
The lemniscate constant can also be computed by the arithmetic–geometric mean
M
{\displaystyle M}
ϖ
=
π
M
(
1
,
2
)
.
{\displaystyle \varpi ={\frac {\pi }{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}.}
Gauss's constant is typically defined as the reciprocal of the arithmetic–geometric mean of 1 and the square root of 2 , after his calculation of
M
(
1
,
2
)
{\displaystyle M{\bigl (}1,{\sqrt {2}}{\bigr )}}
G
=
1
M
(
1
,
2
)
{\displaystyle G={\frac {1}{M{\bigl (}1,{\sqrt {2}}{\bigr )}}}}
beta function B:
A
=
ϖ
2
=
1
4
B
(
1
4
,
1
2
)
,
B
=
π
2
ϖ
=
1
4
B
(
1
2
,
3
4
)
.
{\displaystyle {\begin{aligned}A&={\frac {\varpi }{2}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )},\\B&={\frac {\pi }{2\varpi }}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.\end{aligned}}}
As a special value of L-functions
β
′
(
0
)
=
log
ϖ
π
{\displaystyle \beta '(0)=\log {\frac {\varpi }{\sqrt {\pi }}}}
which is analogous to
ζ
′
(
0
)
=
log
1
2
π
{\displaystyle \zeta '(0)=\log {\frac {1}{\sqrt {2\pi }}}}
where
β
{\displaystyle \beta }
Dirichlet beta function and
ζ
{\displaystyle \zeta }
Riemann zeta function .
Analogously to the Leibniz formula for π ,
β
(
1
)
=
∑
n
=
1
∞
χ
(
n
)
n
=
π
4
,
{\displaystyle \beta (1)=\sum _{n=1}^{\infty }{\frac {\chi (n)}{n}}={\frac {\pi }{4}},}
L
(
E
,
1
)
=
∑
n
=
1
∞
ν
(
n
)
n
=
ϖ
4
{\displaystyle L(E,1)=\sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}={\frac {\varpi }{4}}}
L
{\displaystyle L}
L-function of the elliptic curve
E
:
y
2
=
x
3
−
x
{\displaystyle E:\,y^{2}=x^{3}-x}
Q
{\displaystyle \mathbb {Q} }
ν
{\displaystyle \nu }
multiplicative function given by
ν
(
p
n
)
=
{
p
−
N
p
,
p
∈
P
,
n
=
1
0
,
p
=
2
,
n
≥
2
ν
(
p
)
ν
(
p
n
−
1
)
−
p
ν
(
p
n
−
2
)
,
p
∈
P
∖
{
2
}
,
n
≥
2
{\displaystyle \nu (p^{n})={\begin{cases}p-{\mathcal {N}}_{p},&p\in \mathbb {P} ,\,n=1\\0,&p=2,\,n\geq 2\\\nu (p)\nu (p^{n-1})-p\nu (p^{n-2}),&p\in \mathbb {P} \setminus \{2\},\,n\geq 2\end{cases}}}
N
p
{\displaystyle {\mathcal {N}}_{p}}
a
3
−
a
≡
b
2
(
mod
p
)
,
p
∈
P
{\displaystyle a^{3}-a\equiv b^{2}\,(\operatorname {mod} p),\quad p\in \mathbb {P} }
a
,
b
{\displaystyle a,b}
P
{\displaystyle \mathbb {P} }
ν
{\displaystyle \nu }
F
(
τ
)
=
η
(
4
τ
)
2
η
(
8
τ
)
2
=
∑
n
=
1
∞
ν
(
n
)
q
n
,
q
=
e
2
π
i
τ
{\displaystyle F(\tau )=\eta (4\tau )^{2}\eta (8\tau )^{2}=\sum _{n=1}^{\infty }\nu (n)q^{n},\quad q=e^{2\pi i\tau }}
τ
∈
C
{\displaystyle \tau \in \mathbb {C} }
ℑ
τ
>
0
{\displaystyle \operatorname {\Im } \tau >0}
η
{\displaystyle \eta }
eta function .
The above result can be equivalently written as
∑
n
=
1
∞
ν
(
n
)
n
e
−
2
π
n
/
32
=
ϖ
8
{\displaystyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n}}e^{-2\pi n/{\sqrt {32}}}={\frac {\varpi }{8}}}
32
{\displaystyle 32}
conductor of
E
{\displaystyle E}
BSD conjecture is true for the above
E
{\displaystyle E}
ν
{\displaystyle \nu }
1
≤
n
≤
113
{\displaystyle 1\leq n\leq 113}
n
{\displaystyle n}
ν
(
n
)
=
0
{\displaystyle \nu (n)=0}
n
ν
(
n
)
n
ν
(
n
)
1
1
53
14
5
−
2
61
−
10
9
−
3
65
−
12
13
6
73
−
6
17
2
81
9
25
−
1
85
−
4
29
−
10
89
10
37
−
2
97
18
41
10
101
−
2
45
6
109
6
49
−
7
113
−
14
{\displaystyle {\begin{array}{r|r|r|r}n&\nu (n)&n&\nu (n)\\\hline 1&1&53&14\\5&-2&61&-10\\9&-3&65&-12\\13&6&73&-6\\17&2&81&9\\25&-1&85&-4\\29&-10&89&10\\37&-2&97&18\\41&10&101&-2\\45&6&109&6\\49&-7&113&-14\\\end{array}}}
As a special value of other functions
Let
Δ
{\displaystyle \Delta }
1
{\displaystyle 1}
Δ
(
i
)
=
1
64
(
ϖ
π
)
12
.
{\displaystyle \Delta (i)={\frac {1}{64}}\left({\frac {\varpi }{\pi }}\right)^{12}.}
q
{\displaystyle q}
Δ
{\displaystyle \Delta }
Ramanujan tau function .
Series
Viète's formula for π can be written:
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
An analogous formula for ϖ is:
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
{\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
The Wallis product for π is:
π
2
=
∏
n
=
1
∞
(
1
+
1
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
2
n
2
n
−
1
⋅
2
n
2
n
+
1
)
=
(
2
1
⋅
2
3
)
(
4
3
⋅
4
5
)
(
6
5
⋅
6
7
)
⋯
{\displaystyle {\frac {\pi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right)={\biggl (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\biggr )}{\biggl (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\biggr )}\cdots }
An analogous formula for ϖ is:
ϖ
2
=
∏
n
=
1
∞
(
1
+
1
2
n
)
(
−
1
)
n
+
1
=
∏
n
=
1
∞
(
4
n
−
1
4
n
−
2
⋅
4
n
4
n
+
1
)
=
(
3
2
⋅
4
5
)
(
7
6
⋅
8
9
)
(
11
10
⋅
12
13
)
⋯
{\displaystyle {\frac {\varpi }{2}}=\prod _{n=1}^{\infty }\left(1+{\frac {1}{2n}}\right)^{(-1)^{n+1}}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n-2}}\cdot {\frac {4n}{4n+1}}\right)={\biggl (}{\frac {3}{2}}\cdot {\frac {4}{5}}{\biggr )}{\biggl (}{\frac {7}{6}}\cdot {\frac {8}{9}}{\biggr )}{\biggl (}{\frac {11}{10}}\cdot {\frac {12}{13}}{\biggr )}\cdots }
A related result for Gauss's constant (
G
=
ϖ
/
π
{\displaystyle G=\varpi /\pi }
ϖ
π
=
∏
n
=
1
∞
(
4
n
−
1
4
n
⋅
4
n
+
2
4
n
+
1
)
=
(
3
4
⋅
6
5
)
(
7
8
⋅
10
9
)
(
11
12
⋅
14
13
)
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\prod _{n=1}^{\infty }\left({\frac {4n-1}{4n}}\cdot {\frac {4n+2}{4n+1}}\right)={\biggl (}{\frac {3}{4}}\cdot {\frac {6}{5}}{\biggr )}{\biggl (}{\frac {7}{8}}\cdot {\frac {10}{9}}{\biggr )}{\biggl (}{\frac {11}{12}}\cdot {\frac {14}{13}}{\biggr )}\cdots }
An infinite series discovered by Gauss is:
ϖ
π
=
∑
n
=
0
∞
(
−
1
)
n
∏
k
=
1
n
(
2
k
−
1
)
2
(
2
k
)
2
=
1
−
1
2
2
2
+
1
2
⋅
3
2
2
2
⋅
4
2
−
1
2
⋅
3
2
⋅
5
2
2
2
⋅
4
2
⋅
6
2
+
⋯
{\displaystyle {\frac {\varpi }{\pi }}=\sum _{n=0}^{\infty }(-1)^{n}\prod _{k=1}^{n}{\frac {(2k-1)^{2}}{(2k)^{2}}}=1-{\frac {1^{2}}{2^{2}}}+{\frac {1^{2}\cdot 3^{2}}{2^{2}\cdot 4^{2}}}-{\frac {1^{2}\cdot 3^{2}\cdot 5^{2}}{2^{2}\cdot 4^{2}\cdot 6^{2}}}+\cdots }
The Machin formula for π is
1
4
π
=
4
arctan
1
5
−
arctan
1
239
,
{\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}
1
4
π
=
arctan
1
2
+
arctan
1
3
{\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}}
arcsl
{\displaystyle \operatorname {arcsl} }
lemniscate arcsine .
The lemniscate constant can be rapidly computed by the series
ϖ
=
2
−
1
/
2
π
(
∑
n
∈
Z
e
−
π
n
2
)
2
=
2
1
/
4
π
e
−
π
/
12
(
∑
n
∈
Z
(
−
1
)
n
e
−
π
p
n
)
2
{\displaystyle \varpi =2^{-1/2}\pi {\biggl (}\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}{\biggr )}^{2}=2^{1/4}\pi e^{-\pi /12}{\biggl (}\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi p_{n}}{\biggr )}^{2}}
where
p
n
=
1
2
(
3
n
2
−
n
)
{\displaystyle p_{n}={\tfrac {1}{2}}(3n^{2}-n)}
generalized pentagonal numbers ). Also
∑
m
,
n
∈
Z
e
−
2
π
(
m
2
+
m
n
+
n
2
)
=
1
+
3
ϖ
12
1
/
8
π
.
{\displaystyle \sum _{m,n\in \mathbb {Z} }e^{-2\pi (m^{2}+mn+n^{2})}={\sqrt {1+{\sqrt {3}}}}{\dfrac {\varpi }{12^{1/8}\pi }}.}
In a spirit similar to that of the Basel problem ,
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
=
G
4
(
i
)
=
ϖ
4
15
{\displaystyle \sum _{z\in \mathbb {Z} \setminus \{0\}}{\frac {1}{z^{4}}}=G_{4}(i)={\frac {\varpi ^{4}}{15}}}
where
Z
[
i
]
{\displaystyle \mathbb {Z} }
Gaussian integers and
G
4
{\displaystyle G_{4}}
Eisenstein series of weight
4
{\displaystyle 4}
Lemniscate elliptic functions § Hurwitz numbers for a more general result).
A related result is
∑
n
=
1
∞
σ
3
(
n
)
e
−
2
π
n
=
ϖ
4
80
π
4
−
1
240
{\displaystyle \sum _{n=1}^{\infty }\sigma _{3}(n)e^{-2\pi n}={\frac {\varpi ^{4}}{80\pi ^{4}}}-{\frac {1}{240}}}
where
σ
3
{\displaystyle \sigma _{3}}
sum of positive divisors function .
In 1842, Malmsten found
β
′
(
1
)
=
∑
n
=
1
∞
(
−
1
)
n
+
1
log
(
2
n
+
1
)
2
n
+
1
=
π
4
(
γ
+
2
log
π
ϖ
2
)
{\displaystyle \beta '(1)=\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\log(2n+1)}{2n+1}}={\frac {\pi }{4}}\left(\gamma +2\log {\frac {\pi }{\varpi {\sqrt {2}}}}\right)}
where
γ
{\displaystyle \gamma }
Euler's constant and
β
(
s
)
{\displaystyle \beta (s)}
The lemniscate constant is given by the rapidly converging series
ϖ
=
π
32
4
e
−
π
3
(
∑
n
=
−
∞
∞
(
−
1
)
n
e
−
2
n
π
(
3
n
+
1
)
)
2
.
{\displaystyle \varpi =\pi {\sqrt{32}}e^{-{\frac {\pi }{3}}}{\biggl (}\sum _{n=-\infty }^{\infty }(-1)^{n}e^{-2n\pi (3n+1)}{\biggr )}^{2}.}
The constant is also given by the infinite product
ϖ
=
π
∏
m
=
1
∞
tanh
2
(
π
m
2
)
.
{\displaystyle \varpi =\pi \prod _{m=1}^{\infty }\tanh ^{2}\left({\frac {\pi m}{2}}\right).}
Also
∑
n
=
0
∞
(
−
1
)
n
6635520
n
(
4
n
)
!
n
!
4
=
24
5
7
/
4
ϖ
2
π
2
.
{\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{6635520^{n}}}{\frac {(4n)!}{n!^{4}}}={\frac {24}{5^{7/4}}}{\frac {\varpi ^{2}}{\pi ^{2}}}.}
Continued fractions
A (generalized) continued fraction for π is
π
2
=
1
+
1
1
+
1
⋅
2
1
+
2
⋅
3
1
+
3
⋅
4
1
+
⋱
{\displaystyle {\frac {\pi }{2}}=1+{\cfrac {1}{1+{\cfrac {1\cdot 2}{1+{\cfrac {2\cdot 3}{1+{\cfrac {3\cdot 4}{1+\ddots }}}}}}}}}
ϖ
2
=
1
+
1
2
+
2
⋅
3
2
+
4
⋅
5
2
+
6
⋅
7
2
+
⋱
{\displaystyle {\frac {\varpi }{2}}=1+{\cfrac {1}{2+{\cfrac {2\cdot 3}{2+{\cfrac {4\cdot 5}{2+{\cfrac {6\cdot 7}{2+\ddots }}}}}}}}}
Define Brouncker 's continued fraction
b
(
s
)
=
s
+
1
2
2
s
+
3
2
2
s
+
5
2
2
s
+
⋱
,
s
>
0.
{\displaystyle b(s)=s+{\cfrac {1^{2}}{2s+{\cfrac {3^{2}}{2s+{\cfrac {5^{2}}{2s+\ddots }}}}}},\quad s>0.}
n
≥
0
{\displaystyle n\geq 0}
n
≥
1
{\displaystyle n\geq 1}
b
(
4
n
)
=
(
4
n
+
1
)
∏
k
=
1
n
(
4
k
−
1
)
2
(
4
k
−
3
)
(
4
k
+
1
)
π
ϖ
2
b
(
4
n
+
1
)
=
(
2
n
+
1
)
∏
k
=
1
n
(
2
k
)
2
(
2
k
−
1
)
(
2
k
+
1
)
4
π
b
(
4
n
+
2
)
=
(
4
n
+
1
)
∏
k
=
1
n
(
4
k
−
3
)
(
4
k
+
1
)
(
4
k
−
1
)
2
ϖ
2
π
b
(
4
n
+
3
)
=
(
2
n
+
1
)
∏
k
=
1
n
(
2
k
−
1
)
(
2
k
+
1
)
(
2
k
)
2
π
.
{\displaystyle {\begin{aligned}b(4n)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-1)^{2}}{(4k-3)(4k+1)}}{\frac {\pi }{\varpi ^{2}}}\\b(4n+1)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k)^{2}}{(2k-1)(2k+1)}}{\frac {4}{\pi }}\\b(4n+2)&=(4n+1)\prod _{k=1}^{n}{\frac {(4k-3)(4k+1)}{(4k-1)^{2}}}{\frac {\varpi ^{2}}{\pi }}\\b(4n+3)&=(2n+1)\prod _{k=1}^{n}{\frac {(2k-1)(2k+1)}{(2k)^{2}}}\,\pi .\end{aligned}}}
b
(
1
)
=
4
π
,
b
(
2
)
=
ϖ
2
π
,
b
(
3
)
=
π
,
b
(
4
)
=
9
π
ϖ
2
.
{\displaystyle {\begin{aligned}b(1)&={\frac {4}{\pi }},&b(2)&={\frac {\varpi ^{2}}{\pi }},&b(3)&=\pi ,&b(4)&={\frac {9\pi }{\varpi ^{2}}}.\end{aligned}}}
In fact, the values of
b
(
1
)
{\displaystyle b(1)}
b
(
2
)
{\displaystyle b(2)}
b
(
s
+
2
)
=
(
s
+
1
)
2
b
(
s
)
,
{\displaystyle b(s+2)={\frac {(s+1)^{2}}{b(s)}},}
b
(
n
)
{\displaystyle b(n)}
n
{\displaystyle n}
Simple continued fractions
Simple continued fractions for the lemniscate constant and related constants include
ϖ
=
[
2
,
1
,
1
,
1
,
1
,
1
,
4
,
1
,
2
,
…
]
,
2
ϖ
=
[
5
,
4
,
10
,
2
,
1
,
2
,
3
,
29
,
…
]
,
ϖ
2
=
[
1
,
3
,
4
,
1
,
1
,
1
,
5
,
2
,
…
]
,
ϖ
π
=
[
0
,
1
,
5
,
21
,
3
,
4
,
14
,
…
]
.
{\displaystyle {\begin{aligned}\varpi &=,\\2\varpi &=,\\{\frac {\varpi }{2}}&=,\\{\frac {\varpi }{\pi }}&=.\end{aligned}}}
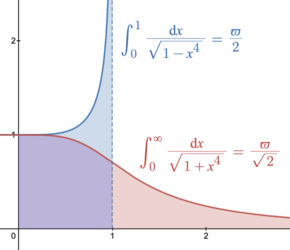
Integrals
A geometric representation of
ϖ
/
2
{\displaystyle \varpi /2}
ϖ
/
2
{\displaystyle \varpi /{\sqrt {2}}}
The lemniscate constant ϖ is related to the area under the curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
π
n
:=
B
(
1
n
,
1
n
)
{\displaystyle \pi _{n}\mathrel {:=} \mathrm {B} {\bigl (}{\tfrac {1}{n}},{\tfrac {1}{n}}{\bigr )}}
x
n
+
y
n
=
1
{\displaystyle x^{n}+y^{n}=1}
2
∫
0
1
1
−
x
n
n
d
x
=
1
n
π
n
.
{\textstyle 2\int _{0}^{1}{\sqrt{1-x^{n}}}\mathop {\mathrm {d} x} ={\tfrac {1}{n}}\pi _{n}.}
1
4
π
4
=
1
2
ϖ
.
{\displaystyle {\tfrac {1}{4}}\pi _{4}={\tfrac {1}{\sqrt {2}}}\varpi .}
In 1842, Malmsten discovered that
∫
0
1
log
(
−
log
x
)
1
+
x
2
d
x
=
π
2
log
π
ϖ
2
.
{\displaystyle \int _{0}^{1}{\frac {\log(-\log x)}{1+x^{2}}}\,dx={\frac {\pi }{2}}\log {\frac {\pi }{\varpi {\sqrt {2}}}}.}
Furthermore,
∫
0
∞
tanh
x
x
e
−
x
d
x
=
log
ϖ
2
π
{\displaystyle \int _{0}^{\infty }{\frac {\tanh x}{x}}e^{-x}\,dx=\log {\frac {\varpi ^{2}}{\pi }}}
and
∫
0
∞
e
−
x
4
d
x
=
2
ϖ
2
π
4
,
analogous to
∫
0
∞
e
−
x
2
d
x
=
π
2
,
{\displaystyle \int _{0}^{\infty }e^{-x^{4}}\,dx={\frac {\sqrt {2\varpi {\sqrt {2\pi }}}}{4}},\quad {\text{analogous to}}\,\int _{0}^{\infty }e^{-x^{2}}\,dx={\frac {\sqrt {\pi }}{2}},}
Gaussian integral .
The lemniscate constant appears in the evaluation of the integrals
π
ϖ
=
∫
0
π
2
sin
(
x
)
d
x
=
∫
0
π
2
cos
(
x
)
d
x
{\displaystyle {\frac {\pi }{\varpi }}=\int _{0}^{\frac {\pi }{2}}{\sqrt {\sin(x)}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos(x)}}\,dx}
ϖ
π
=
∫
0
∞
d
x
cosh
(
π
x
)
{\displaystyle {\frac {\varpi }{\pi }}=\int _{0}^{\infty }{\frac {dx}{\sqrt {\cosh(\pi x)}}}}
John Todd's lemniscate constants are defined by integrals:
A
=
∫
0
1
d
x
1
−
x
4
{\displaystyle A=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}
B
=
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle B=\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Circumference of an ellipse
The lemniscate constant satisfies the equation
π
ϖ
=
2
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle {\frac {\pi }{\varpi }}=2\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Euler discovered in 1738 that for the rectangular elastica (first and second lemniscate constants)
arc
length
⋅
height
=
A
⋅
B
=
∫
0
1
d
x
1
−
x
4
⋅
∫
0
1
x
2
d
x
1
−
x
4
=
ϖ
2
⋅
π
2
ϖ
=
π
4
{\displaystyle {\textrm {arc}}\ {\textrm {length}}\cdot {\textrm {height}}=A\cdot B=\int _{0}^{1}{\frac {\mathrm {d} x}{\sqrt {1-x^{4}}}}\cdot \int _{0}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}={\frac {\varpi }{2}}\cdot {\frac {\pi }{2\varpi }}={\frac {\pi }{4}}}
Now considering the circumference
C
{\displaystyle C}
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
2
x
2
+
4
y
2
=
1
{\displaystyle 2x^{2}+4y^{2}=1}
C
2
=
∫
0
1
d
x
1
−
x
4
+
∫
0
1
x
2
d
x
1
−
x
4
{\displaystyle {\frac {C}{2}}=\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}+\int _{0}^{1}{\frac {x^{2}\,dx}{\sqrt {1-x^{4}}}}}
Hence the full circumference is
C
=
π
ϖ
+
ϖ
=
3.820197789
…
{\displaystyle C={\frac {\pi }{\varpi }}+\varpi =3.820197789\ldots }
This is also the arc length of the sine curve on half a period:
C
=
∫
0
π
1
+
cos
2
(
x
)
d
x
{\displaystyle C=\int _{0}^{\pi }{\sqrt {1+\cos ^{2}(x)}}\,dx}
Other limits
Analogously to
2
π
=
lim
n
→
∞
|
(
2
n
)
!
B
2
n
|
1
2
n
{\displaystyle 2\pi =\lim _{n\to \infty }\left|{\frac {(2n)!}{\mathrm {B} _{2n}}}\right|^{\frac {1}{2n}}}
B
n
{\displaystyle \mathrm {B} _{n}}
Bernoulli numbers , we have
2
ϖ
=
lim
n
→
∞
(
(
4
n
)
!
H
4
n
)
1
4
n
{\displaystyle 2\varpi =\lim _{n\to \infty }\left({\frac {(4n)!}{\mathrm {H} _{4n}}}\right)^{\frac {1}{4n}}}
H
n
{\displaystyle \mathrm {H} _{n}}
Hurwitz numbers .
Notes
Finch 2003 , p. 420Kobayashi, Hiroyuki; Takeuchi, Shingo (2019), "Applications of generalized trigonometric functions with two parameters", Communications on Pure & Applied Analysis , 18 (3): 1509–1521, arXiv :1903.07407 , doi :10.3934/cpaa.2019072 , S2CID 102487670 Asai, Tetsuya (2007), Elliptic Gauss Sums and Hecke L-values at s=1 , arXiv :0707.3711 "A062539 - Oeis" ."A064853 - Oeis" ."Lemniscate Constant" ."Records set by y-cruncher" . numberworld.org . Retrieved 2024-08-20."A014549 - Oeis" .Finch 2003 , p. 420.
Cox 1984 , p. 281
^ Todd, John (January 1975). "The lemniscate constants" . Communications of the ACM 18 (1): 14–19. doi :10.1145/360569.360580 . S2CID 85873 .
^ "A085565 - Oeis" ."A076390 - Oeis" .
Carlson, B. C. (2010), "Elliptic Integrals" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 .
G
4
(
ω
1
,
ω
2
)
{\displaystyle \operatorname {G} _{4}(\omega _{1},\omega _{2})}
G
6
(
ω
1
,
ω
2
)
{\displaystyle \operatorname {G} _{6}(\omega _{1},\omega _{2})}
Im
(
ω
2
/
ω
1
)
>
0
{\displaystyle \operatorname {Im} (\omega _{2}/\omega _{1})>0}
ω
1
{\displaystyle \omega _{1}}
ω
2
{\displaystyle \omega _{2}}
G
4
{\displaystyle \operatorname {G} _{4}}
G
6
{\displaystyle \operatorname {G} _{6}}
Eisenstein series . The fact that
ϖ
{\displaystyle \varpi }
G
4
(
ϖ
,
ϖ
i
)
=
1
/
15
{\displaystyle \operatorname {G} _{4}(\varpi ,\varpi i)=1/15}
G
6
(
ϖ
,
ϖ
i
)
=
0.
{\displaystyle \operatorname {G} _{6}(\varpi ,\varpi i)=0.}
Apostol, T. M. (1990). Modular Functions and Dirichlet Series in Number Theory (Second ed.). Springer. p. 12. ISBN 0-387-97127-0 Siegel, C. L. (1932). "Über die Perioden elliptischer Funktionen" . Journal für die reine und angewandte Mathematik 167 : 62–69. doi :10.1515/crll.1932.167.62 .
beta function
B
(
a
,
b
)
{\displaystyle \mathrm {B} (a,b)}
a
,
b
∈
Q
∖
Z
{\displaystyle a,b\in \mathbb {Q} \setminus \mathbb {Z} }
a
+
b
∉
Z
0
−
{\displaystyle a+b\notin \mathbb {Z} _{0}^{-}}
ϖ
{\displaystyle \varpi }
ϖ
=
1
2
B
(
1
4
,
1
2
)
{\displaystyle \varpi ={\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{2}}{\bigr )}}
B
(
1
2
,
3
4
)
.
{\displaystyle \mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {3}{4}}{\bigr )}.}
Schneider, Theodor (1941). "Zur Theorie der Abelschen Funktionen und Integrale" . Journal für die reine und angewandte Mathematik . 183 (19): 110–128. doi :10.1515/crll.1941.183.110 . S2CID 118624331 .
Algebraic independence of constants connected with the functions of analysis , Notices of the AMS 22, 1975, p. A-486
Contributions to The Theory of Transcendental Numbers , American Mathematical Society, 1984, p. 6
π
=
2
2
M
3
(
1
,
1
2
)
M
′
(
1
,
1
2
)
=
1
G
3
M
′
(
1
,
1
2
)
.
{\displaystyle \pi =2{\sqrt {2}}{\frac {M^{3}\left(1,{\frac {1}{\sqrt {2}}}\right)}{M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}={\frac {1}{G^{3}M'\left(1,{\frac {1}{\sqrt {2}}}\right)}}.}
Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience. ISBN 0-471-83138-7 p. 45
Nesterenko, Y. V.; Philippon, P. (2001). Introduction to Algebraic Independence Theory . Springer. p. 27. ISBN 3-540-41496-7
Cox 1984 , p. 277.
"A113847 - Oeis" .Cremona, J. E. (1997). Algorithms for Modular Elliptic Curves Cambridge University Press . ISBN 0521598206 p. 31, formula (2.8.10)
∑
n
=
1
∞
ν
(
n
)
n
s
{\textstyle \sum _{n=1}^{\infty }{\frac {\nu (n)}{n^{s}}}}
ℜ
s
>
5
/
6
{\displaystyle \operatorname {\Re } s>5/6}
Murty, Vijaya Kumar (1995). Seminar on Fermat's Last Theorem . American Mathematical Society . p. 16. ISBN 9780821803134 Cohen, Henri (1993). A Course in Computational Algebraic Number Theory . Springer-Verlag. pp. 382–406. ISBN 978-3-642-08142-2 "Elliptic curve with LMFDB label 32.a3 (Cremona label 32a2)" . The L-functions and modular forms database .
F
{\displaystyle F}
2
{\displaystyle 2}
32
{\displaystyle 32}
new form and it satisfies the functional equation
F
(
−
1
τ
)
=
−
τ
2
32
F
(
τ
1
32
)
.
{\displaystyle F\left(-{\frac {1}{\tau }}\right)=-{\frac {\tau ^{2}}{32}}F\left({\frac {\tau {\vphantom {1}}}{32}}\right).}
ν
{\displaystyle \nu }
ξ
{\displaystyle \xi }
ξ
(
p
n
)
=
{
N
p
′
,
p
∈
P
,
n
=
1
ξ
(
p
n
−
1
)
+
χ
(
p
)
n
,
p
∈
P
,
n
≥
2
{\displaystyle \xi (p^{n})={\begin{cases}{\mathcal {N}}_{p}',&p\in \mathbb {P} ,\,n=1\\\xi (p^{n-1})+\chi (p)^{n},&p\in \mathbb {P} ,\,n\geq 2\end{cases}}}
N
p
′
{\displaystyle {\mathcal {N}}_{p}'}
a
2
+
b
2
=
p
,
p
∈
P
{\displaystyle a^{2}+b^{2}=p,\quad p\in \mathbb {P} }
a
,
b
{\displaystyle a,b}
Fermat's theorem on sums of two squares ) and
χ
{\displaystyle \chi }
Dirichlet character from the Leibniz formula for π; also
∑
d
|
n
χ
(
d
)
=
ξ
(
n
)
{\displaystyle \sum _{d|n}\chi (d)=\xi (n)}
n
{\displaystyle n}
ν
{\displaystyle \nu }
ξ
{\displaystyle \xi }
∑
k
=
0
n
(
−
1
)
k
ξ
(
4
k
+
1
)
ξ
(
4
n
−
4
k
+
1
)
=
ν
(
2
n
+
1
)
{\displaystyle \sum _{k=0}^{n}(-1)^{k}\xi (4k+1)\xi (4n-4k+1)=\nu (2n+1)}
n
{\displaystyle n}
ν
{\displaystyle \nu }
∑
z
∈
G
;
z
z
¯
=
n
z
=
ν
(
n
)
{\displaystyle \sum _{z\in \mathbb {G} ;\,z{\overline {z}}=n}z=\nu (n)}
n
{\displaystyle n}
G
{\displaystyle \operatorname {\mathbb {G} } }
Gaussian integers of the form
(
−
1
)
a
±
b
−
1
2
(
a
±
b
i
)
{\displaystyle (-1)^{\frac {a\pm b-1}{2}}(a\pm bi)}
a
{\displaystyle a}
b
{\displaystyle b}
ξ
{\displaystyle \xi }
|
{
z
:
z
∈
G
∧
z
z
¯
=
n
}
|
=
ξ
(
n
)
{\displaystyle \left|\{z:z\in \mathbb {G} \land z{\overline {z}}=n\}\right|=\xi (n)}
n
{\displaystyle n}
Rubin, Karl (1987). "Tate-Shafarevich groups and L-functions of elliptic curves with complex multiplication" . Inventiones Mathematicae . 89 (3): 528. Bibcode :1987InMat..89..527R . doi :10.1007/BF01388984 .
"Newform orbit 1.12.a.a" . The L-functions and modular forms database .Hyde, Trevor (2014). "A Wallis product on clovers" (PDF). The American Mathematical Monthly . 121 (3): 237–243. doi :10.4169/amer.math.monthly.121.03.237 . S2CID 34819500 .
Bottazzini, Umberto ; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 Cox 1984 , p. 307, eq. 2.21 for the first equality. The second equality can be proved by using the pentagonal number theorem .
Berndt, Bruce C. (1998). Ramanujan's Notebooks Part V . Springer. ISBN 978-1-4612-7221-2 p. 326
hypergeometric inversion : Let
a
(
q
)
=
∑
m
,
n
∈
Z
q
m
2
+
m
n
+
n
2
{\displaystyle \operatorname {a} (q)=\sum _{m,n\in \mathbb {Z} }q^{m^{2}+mn+n^{2}}}
q
∈
C
{\displaystyle q\in \mathbb {C} }
|
q
|
<
1
{\displaystyle \left|q\right|<1}
a
(
q
)
=
2
F
1
(
1
3
,
2
3
,
1
,
z
)
{\displaystyle \operatorname {a} (q)={}_{2}F_{1}\left({\frac {1}{3}},{\frac {2}{3}},1,z\right)}
q
=
exp
(
−
2
π
3
2
F
1
(
1
/
3
,
2
/
3
,
1
,
1
−
z
)
2
F
1
(
1
/
3
,
2
/
3
,
1
,
z
)
)
{\displaystyle q=\exp \left(-{\frac {2\pi }{\sqrt {3}}}{\frac {{}_{2}F_{1}(1/3,2/3,1,1-z)}{{}_{2}F_{1}(1/3,2/3,1,z)}}\right)}
z
∈
C
∖
{
0
,
1
}
{\displaystyle z\in \mathbb {C} \setminus \{0,1\}}
z
=
1
4
(
3
3
−
5
)
{\textstyle z={\tfrac {1}{4}}{\bigl (}3{\sqrt {3}}-5{\bigr )}}
Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi . American Mathematical Society. ISBN 0-8218-3246-8 p. 232
Garrett, Paul. "Level-one elliptic modular forms" (PDF). University of Minnesota . p. 11—13
hypergeometric transformation
3
F
2
(
1
4
,
1
2
,
3
4
,
1
,
1
,
16
z
(
1
−
z
)
2
(
1
+
z
)
4
)
=
(
1
+
z
)
2
F
1
(
1
2
,
1
2
,
1
,
z
)
2
{\displaystyle {}_{3}F_{2}\left({\frac {1}{4}},{\frac {1}{2}},{\frac {3}{4}},1,1,16z{\frac {(1-z)^{2}}{(1+z)^{4}}}\right)=(1+z)\,{}_{2}F_{1}\left({\frac {1}{2}},{\frac {1}{2}},1,z\right)^{2}}
z
=
λ
(
1
+
5
i
)
{\displaystyle z=\lambda (1+5i)}
λ
{\displaystyle \lambda }
modular lambda function .
Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1 p. 140 (eq. 3.34), p. 153. There's an error on p. 153:
4
[
Γ
(
3
+
s
/
4
)
/
Γ
(
1
+
s
/
4
)
]
2
{\displaystyle 4^{2}}
4
[
Γ
(
(
3
+
s
)
/
4
)
/
Γ
(
(
1
+
s
)
/
4
)
]
2
{\displaystyle 4^{2}}
Khrushchev, Sergey (2008). Orthogonal Polynomials and Continued Fractions (First ed.). Cambridge University Press. ISBN 978-0-521-85419-1 p. 146, 155
Perron, Oskar (1957). Die Lehre von den Kettenbrüchen: Band II (in German) (Third ed.). B. G. Teubner."A062540 - OEIS" . oeis.org . Retrieved 2022-09-14."A053002 - OEIS" . oeis.org .Blagouchine, Iaroslav V. (2014). "Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results" . The Ramanujan Journal . 35 (1): 21–110. doi :10.1007/s11139-013-9528-5 . S2CID 120943474 .
"A068467 - Oeis" .^ Cox 1984 , p. 313.
Cox 1984 , p. 312.
Adlaj, Semjon (2012). "An Eloquent Formula for the Perimeter of an Ellipse" (PDF). American Mathematical Society . p. 1097. One might also observe that the length of the "sine" curve over half a period, that is, the length of the graph of the function
sin
(
t
)
{\displaystyle \sin(t)}
t
=
0
{\displaystyle t=0}
t
=
π
{\displaystyle t=\pi }
2
l
(
1
/
2
)
=
L
+
M
{\displaystyle {\sqrt {2}}l(1/{\sqrt {2}})=L+M}
In this paper
M
=
1
/
G
=
π
/
ϖ
{\displaystyle M=1/G=\pi /\varpi }
L
=
π
/
M
=
G
π
=
ϖ
{\displaystyle L=\pi /M=G\pi =\varpi }
References
External links
Categories :


 is 2ϖ. The lemniscate constant is closely related to the
is 2ϖ. The lemniscate constant is closely related to the  . By 1799, Gauss had two proofs of the theorem that
. By 1799, Gauss had two proofs of the theorem that  where
where  is the lemniscate constant.
is the lemniscate constant.
 were proven
were proven  and Gauss's constant
and Gauss's constant  were proven transcendental by Theodor Schneider in 1941. In 1975,
were proven transcendental by Theodor Schneider in 1941. In 1975,  is
is  , which implies that
, which implies that  (where the prime denotes the
(where the prime denotes the  is algebraically independent over
is algebraically independent over 
 ,
,

 published in 1800:
published in 1800: John Todd's lemniscate constants may be given in terms of the
John Todd's lemniscate constants may be given in terms of the 


 is the
is the  is the
is the  we have
we have
 where
where  is the
is the  over
over  is the
is the  where
where  is the number of solutions of the congruence
is the number of solutions of the congruence
 in variables
in variables  that are non-negative integers (
that are non-negative integers ( is the set of all primes).
Equivalently,
is the set of all primes).
Equivalently,  where
where  such that
such that  and
and  is the
is the  (the number
(the number  is the
is the  ) and also tells us that the
) and also tells us that the  such that
such that  doesn't appear in the table, then
doesn't appear in the table, then  :
:

 be the minimal weight level
be the minimal weight level  new form. Then
new form. Then
 The
The  -coefficient of
-coefficient of 



 ) is:
) is:


 and several similar formulas for π can be developed using trigonometric angle sum identities, e.g. Euler's formula
and several similar formulas for π can be developed using trigonometric angle sum identities, e.g. Euler's formula  . Analogous formulas can be developed for ϖ, including the following found by Gauss:
. Analogous formulas can be developed for ϖ, including the following found by Gauss:  , where
, where  is the
is the 
 (these are the
(these are the 

 are the
are the  is the
is the  (see
(see 
 is the
is the 
 is
is  is the Dirichlet-Beta function.
is the Dirichlet-Beta function.



 An analogous formula for ϖ is
An analogous formula for ϖ is

 Let
Let  except for the first equality where
except for the first equality where  . Then
. Then
 For example,
For example,

 and
and  , coupled with the functional equation
, coupled with the functional equation
 determine the values of
determine the values of  for all
for all 
 and
and 
 . Defining
. Defining  , twice the area in the positive quadrant under the curve
, twice the area in the positive quadrant under the curve  is
is  In the quartic case,
In the quartic case, 


 a form of
a form of 





 of the ellipse with axes
of the ellipse with axes  and
and  , Stirling noted that
, Stirling noted that



 where
where  are
are  where
where  are
are  and
and  with
with  are algebraic, then
are algebraic, then  or
or  is transcendental. Here,
is transcendental. Here,  and
and  are
are  and
and  Apostol, T. M. (1990). Modular Functions and Dirichlet Series in Number Theory (Second ed.). Springer. p. 12.
Apostol, T. M. (1990). Modular Functions and Dirichlet Series in Number Theory (Second ed.). Springer. p. 12.  is transcendental for all
is transcendental for all  such that
such that  . The fact that
. The fact that  and similarly for B and G from
and similarly for B and G from  Schneider, Theodor (1941).
Schneider, Theodor (1941).  Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience.
Borwein, Jonathan M.; Borwein, Peter B. (1987). Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity (First ed.). Wiley-Interscience.  converges for
converges for  .
.
 is the unique weight
is the unique weight  level
level 
 function which is the multiplicative function defined by
function which is the multiplicative function defined by

 is the number of solutions of the equation
is the number of solutions of the equation

 is the
is the 


 is the set of all
is the set of all 
 is odd and
is odd and  is even. The
is even. The 

 with
with  . Then
. Then


 . The formula in question follows from setting
. The formula in question follows from setting  .
.

 and
and  is the
is the  should be
should be  .
.
 from the point where
from the point where  to the point where
to the point where  , is
, is  .
. and
and  .
.