Metaheuristic in computer science and mathematical optimization is a higher-level procedure or heuristic designed to find, generate, tune, or select a heuristic (partial search algorithm) that may provide a sufficiently good solution to an optimization problem or a machine learning problem, especially with incomplete or imperfect information or limited computation capacity. Metaheuristics sample a subset of solutions which is otherwise too large to be completely enumerated or otherwise explored. Metaheuristics may make relatively few assumptions about the optimization problem being solved and so may be usable for a variety of problems. Their use is always of interest when exact or other (approximate) methods are not available or are not expedient, either because the calculation time is too long or because, for example, the solution provided is too imprecise.
Compared to optimization algorithms and iterative methods, metaheuristics do not guarantee that a globally optimal solution can be found on some class of problems. Many metaheuristics implement some form of stochastic optimization, so that the solution found is dependent on the set of random variables generated. In combinatorial optimization, there are many problems that belong to the class of NP-complete problems and thus can no longer be solved exactly in an acceptable time from a relatively low degree of complexity. Metaheuristics then often provide good solutions with less computational effort than approximation methods, iterative methods, or simple heuristics. This also applies in the field of continuous or mixed-integer optimization. As such, metaheuristics are useful approaches for optimization problems. Several books and survey papers have been published on the subject. Literature review on metaheuristic optimization, suggested that it was Fred Glover who coined the word metaheuristics.
Most literature on metaheuristics is experimental in nature, describing empirical results based on computer experiments with the algorithms. But some formal theoretical results are also available, often on convergence and the possibility of finding the global optimum. Also worth mentioning are the no-free-lunch theorems, which state that there can be no metaheuristic that is better than all others for any given problem.
Especially since the turn of the millennium, many metaheuristic methods have been published with claims of novelty and practical efficacy. While the field also features high-quality research, many of the more recent publications have been of poor quality; flaws include vagueness, lack of conceptual elaboration, poor experiments, and ignorance of previous literature.
Properties
These are properties that characterize most metaheuristics:
- Metaheuristics are strategies that guide the search process.
- The goal is to efficiently explore the search space in order to find optimal or near–optimal solutions.
- Techniques which constitute metaheuristic algorithms range from simple local search procedures to complex learning processes.
- Metaheuristic algorithms are approximate and usually non-deterministic.
- Metaheuristics are not problem-specific. However, they were often developed in relation to a problem class such as continuous or combinatorial optimization and then generalized later in some cases.
- They can draw on domain-specific knowledge in the form of heuristics that are controlled by a higher-level strategy of the metaheuristic.
- They can contain mechanisms that prevent them from getting stuck in certain areas of the search space.
- Modern metaheuristics often use the search history to control the search.
Classification
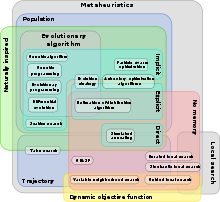
There are a wide variety of metaheuristics and a number of properties with respect to which to classify them. The following list is therefore to be understood as an example.
Local search vs. global search
One approach is to characterize the type of search strategy. One type of search strategy is an improvement on simple local search algorithms. A well known local search algorithm is the hill climbing method which is used to find local optimums. However, hill climbing does not guarantee finding global optimum solutions.
Many metaheuristic ideas were proposed to improve local search heuristic in order to find better solutions. Such metaheuristics include simulated annealing, tabu search, iterated local search, variable neighborhood search, and GRASP. These metaheuristics can both be classified as local search-based or global search metaheuristics.
Other global search metaheuristic that are not local search-based are usually population-based metaheuristics. Such metaheuristics include ant colony optimization, evolutionary computation such as genetic algorithm or evolution strategies, particle swarm optimization, rider optimization algorithm and bacterial foraging algorithm.
Single-solution vs. population-based
Another classification dimension is single solution vs population-based searches. Single solution approaches focus on modifying and improving a single candidate solution; single solution metaheuristics include simulated annealing, iterated local search, variable neighborhood search, and guided local search. Population-based approaches maintain and improve multiple candidate solutions, often using population characteristics to guide the search; population based metaheuristics include evolutionary computation and particle swarm optimization. Another category of metaheuristics is Swarm intelligence which is a collective behavior of decentralized, self-organized agents in a population or swarm. Ant colony optimization, particle swarm optimization, social cognitive optimization and bacterial foraging algorithm are examples of this category.
Hybridization and memetic algorithms
A hybrid metaheuristic is one that combines a metaheuristic with other optimization approaches, such as algorithms from mathematical programming, constraint programming, and machine learning. Both components of a hybrid metaheuristic may run concurrently and exchange information to guide the search.
On the other hand, Memetic algorithms represent the synergy of evolutionary or any population-based approach with separate individual learning or local improvement procedures for problem search. An example of memetic algorithm is the use of a local search algorithm instead of or in addition to a basic mutation operator in evolutionary algorithms.
Parallel metaheuristics
A parallel metaheuristic is one that uses the techniques of parallel programming to run multiple metaheuristic searches in parallel; these may range from simple distributed schemes to concurrent search runs that interact to improve the overall solution.
With population-based metaheuristics, the population itself can be parallelized by either processing each individual or group with a separate thread or the metaheuristic itself runs on one computer and the offspring are evaluated in a distributed manner per iteration. The latter is particularly useful if the computational effort for the evaluation is considerably greater than that for the generation of descendants. This is the case in many practical applications, especially in simulation-based calculations of solution quality.
Nature-inspired and metaphor-based metaheuristics
Main articles: Swarm intelligence and List of metaphor-inspired metaheuristicsA very active area of research is the design of nature-inspired metaheuristics. Many recent metaheuristics, especially evolutionary computation-based algorithms, are inspired by natural systems. Nature acts as a source of concepts, mechanisms and principles for designing of artificial computing systems to deal with complex computational problems. Such metaheuristics include simulated annealing, evolutionary algorithms, ant colony optimization and particle swarm optimization.
A large number of more recent metaphor-inspired metaheuristics have started to attract criticism in the research community for hiding their lack of novelty behind an elaborate metaphor. As a result, a number of renowned scientists of the field have proposed a research agenda for the standardization of metaheuristics in order to make them more comparable, among other things. Another consequence is that the publication guidelines of a number of scientific journals have been adapted accordingly.
Applications
Most metaheuristics are search methods and when using them, the evaluation function should be subject to greater demands than a mathematical optimization. Not only does the desired target state have to be formulated, but the evaluation should also reward improvements to a solution on the way to the target in order to support and accelerate the search process. The fitness functions of evolutionary or memetic algorithms can serve as an example.
Metaheuristics are used for all types of optimization problems, ranging from continuous through mixed integer problems to combinatorial optimization or combinations thereof. In combinatorial optimization, an optimal solution is sought over a discrete search-space. An example problem is the travelling salesman problem where the search-space of candidate solutions grows faster than exponentially as the size of the problem increases, which makes an exhaustive search for the optimal solution infeasible. Additionally, multidimensional combinatorial problems, including most design problems in engineering such as form-finding and behavior-finding, suffer from the curse of dimensionality, which also makes them infeasible for exhaustive search or analytical methods.
Metaheuristics are also frequently applied to scheduling problems. A typical representative of this combinatorial task class is job shop scheduling, which involves assigning the work steps of jobs to processing stations in such a way that all jobs are completed on time and altogether in the shortest possible time. In practice, restrictions often have to be observed, e.g. by limiting the permissible sequence of work steps of a job through predefined workflows and/or with regard to resource utilisation, e.g. in the form of smoothing the energy demand. Popular metaheuristics for combinatorial problems include genetic algorithms by Holland et al., scatter search and tabu search by Glover.
Another large field of application are optimization tasks in continuous or mixed-integer search spaces. This includes, e.g., design optimization or various engineering tasks. An example of the mixture of combinatorial and continuous optimization is the planning of favourable motion paths for industrial robots.
Metaheuristic Optimization Frameworks
A MOF can be defined as ‘‘a set of software tools that provide a correct and reusable implementation of a set of metaheuristics, and the basic mechanisms to accelerate the implementation of its partner subordinate heuristics (possibly including solution encodings and technique-specific operators), which are necessary to solve a particular problem instance using techniques provided’’.
There are many candidate optimization tools which can be considered as a MOF of varying feature. The following list of 33 MOFs is compared and evaluated in detail in: Comet, EvA2, evolvica, Evolutionary::Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO, Pisa, Watchmaker, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Optimization Algorithm Toolkit, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA, and UOF. There have been a number of publications on the support of parallel implementations, which was missing in this comparative study, particularly from the late 10s onwards.
Contributions
Many different metaheuristics are in existence and new variants are continually being proposed. Some of the most significant contributions to the field are:
- 1952: Robbins and Monro work on stochastic optimization methods.
- 1954: Barricelli carries out the first simulations of the evolution process and uses them on general optimization problems.
- 1963: Rastrigin proposes random search.
- 1965: Matyas proposes random optimization.
- 1965: Nelder and Mead propose a simplex heuristic, which was shown by Powell to converge to non-stationary points on some problems.
- 1965: Ingo Rechenberg discovers the first Evolution Strategies algorithm.
- 1966: Fogel et al. propose evolutionary programming.
- 1970: Hastings proposes the Metropolis–Hastings algorithm.
- 1970: Cavicchio proposes adaptation of control parameters for an optimizer.
- 1970: Kernighan and Lin propose a graph partitioning method, related to variable-depth search and prohibition-based (tabu) search.
- 1975: Holland proposes the genetic algorithm.
- 1977: Glover proposes scatter search.
- 1978: Mercer and Sampson propose a metaplan for tuning an optimizer's parameters by using another optimizer.
- 1980: Smith describes genetic programming.
- 1983: Kirkpatrick et al. propose simulated annealing.
- 1986: Glover proposes tabu search, first mention of the term metaheuristic.
- 1989: Moscato proposes memetic algorithms.
- 1990: Moscato and Fontanari, and Dueck and Scheuer, independently proposed a deterministic update rule for simulated annealing which accelerated the search. This led to the threshold accepting metaheuristic.
- 1992: Dorigo introduces ant colony optimization in his PhD thesis.
- 1995: Wolpert and Macready prove the no free lunch theorems.
See also
- Stochastic search
- Meta-optimization
- Matheuristics
- Hyper-heuristics
- Swarm intelligence
- Evolutionary algorithms and in particular genetic algorithms, genetic programming, or evolution strategies.
- Simulated annealing
- Workforce modeling
References
- ^ Glover, F.; Kochenberger, G.A. (2003). Handbook of metaheuristics. Vol. 57. Springer, International Series in Operations Research & Management Science. ISBN 978-1-4020-7263-5.
- R. Balamurugan; A.M. Natarajan; K. Premalatha (2015). "Stellar-Mass Black Hole Optimization for Biclustering Microarray Gene Expression Data". Applied Artificial Intelligence. 29 (4): 353–381. doi:10.1080/08839514.2015.1016391. S2CID 44624424.
- ^ Bianchi, Leonora; Marco Dorigo; Luca Maria Gambardella; Walter J. Gutjahr (2009). "A survey on metaheuristics for stochastic combinatorial optimization" (PDF). Natural Computing. 8 (2): 239–287. doi:10.1007/s11047-008-9098-4. S2CID 9141490.
- ^ Blum, Christian; Roli, Andrea (2003). "Metaheuristics in combinatorial optimization: Overview and conceptual comparison". ACM Computing Surveys. 35 (3). ACM: 268–308. doi:10.1145/937503.937505.
- ^ Jarboui, Bassem; Siarry, Patrick; Teghem, Jacques, eds. (2013). Metaheuristics for production scheduling. Automation - control and industrial engineering series. London: ISTE. ISBN 978-1-84821-497-2.
- ^ Gupta, Shubham; Abderazek, Hammoudi; Yıldız, Betül Sultan; Yildiz, Ali Riza; Mirjalili, Seyedali; Sait, Sadiq M. (2021). "Comparison of metaheuristic optimization algorithms for solving constrained mechanical design optimization problems". Expert Systems with Applications. 183: 115351. doi:10.1016/j.eswa.2021.115351.
- Brucker, Peter; Knust, Sigrid (2012). Complex Scheduling. Berlin, Heidelberg: Springer. doi:10.1007/978-3-642-23929-8. ISBN 978-3-642-23928-1.
- Papadimitriou, Christos H.; Steiglitz, Kenneth (1998). Combinatorial Optimization: Algorithms and Complexity. Mineola, N.Y: Dover Publ., corrected, unabridged new edition of the work published by Prentice-Hall in 1982. ISBN 978-0-486-40258-1.
- ^ Gad, Ahmed G. (2022). "Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review". Archives of Computational Methods in Engineering. 29 (5): 2531–2561. doi:10.1007/s11831-021-09694-4. ISSN 1134-3060.
- Li, Zhenhua; Lin, Xi; Zhang, Qingfu; Liu, Hailin (2020). "Evolution strategies for continuous optimization: A survey of the state-of-the-art". Swarm and Evolutionary Computation. 56: 100694. doi:10.1016/j.swevo.2020.100694.
- Goldberg, D.E. (1989). Genetic Algorithms in Search, Optimization and Machine Learning. Kluwer Academic Publishers. ISBN 978-0-201-15767-3.
- ^ Talbi, E-G. (2009). Metaheuristics: from design to implementation. Wiley. ISBN 978-0-470-27858-1.
- X. S. Yang, Metaheuristic optimization, Scholarpedia, 6(8):11472 (2011).
- Glover, Fred (January 1986). "Future paths for integer programming and links to artificial intelligence" (PDF). Computers and Operations Research. 13 (5): 533–549. doi:10.1016/0305-0548(86)90048-1. ISSN 0305-0548.
- Rudolph, Günter (2001). "Self-adaptive mutations may lead to premature convergence". IEEE Transactions on Evolutionary Computation. 5 (4): 410–414. doi:10.1109/4235.942534. hdl:2003/5378.
- ^ Sörensen, Kenneth (2015). "Metaheuristics—the metaphor exposed". International Transactions in Operational Research. 22 (1): 3–18. CiteSeerX 10.1.1.470.3422. doi:10.1111/itor.12001. S2CID 14042315.
- ^ Brownlee, Alexander; Woodward, John R. "Why we fell out of love with algorithms inspired by nature". The Conversation (website). Retrieved 2024-08-30.
- Schwefel, Hans-Paul (1995). Evolution and optimum seeking. Sixth-generation computer technology series. New York: Wiley. ISBN 978-0-471-57148-3.
- Eberhart, R.; Kennedy, J. (1995), "A new optimizer using particle swarm theory", Conf. Proc. MHS'95, IEEE, pp. 39–43, doi:10.1109/MHS.1995.494215, ISBN 978-0-7803-2676-7
- Colorni, Alberto; Dorigo, Marco; Maniezzo, Vittorio (1991), Varela, F.; Bourgine, P. (eds.), "Distributed Optimization by Ant Colonies", Conf. Proc. of ECAL91 - European Conference on Artificial Life, Amsterdam: Elsevier Publ., pp. 134–142, ISBN 9780262720199
- Socha, Krzysztof; Dorigo, Marco (2008). "Ant colony optimization for continuous domains". European Journal of Operational Research. 185 (3): 1155–1173. doi:10.1016/j.ejor.2006.06.046.
- Nissen, Volker; Krause, Matthias (1994), Reusch, Bernd (ed.), "Constrained Combinatorial Optimization with an Evolution Strategy", Fuzzy Logik, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 33–40, doi:10.1007/978-3-642-79386-8_5, ISBN 978-3-540-58649-4, retrieved 2024-08-24
- Classification of metaheuristics
- Raidl, Günther R. (2006), Almeida, Francisco; Blesa Aguilera, María J.; Blum, Christian; Moreno Vega, José Marcos (eds.), "A Unified View on Hybrid Metaheuristics", Hybrid Metaheuristics, Lecture Notes in Computer Science, vol. 4030, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 1–12, doi:10.1007/11890584_1, ISBN 978-3-540-46384-9, retrieved 2024-08-24
- ^ Glover, Fred; Sörensen, Kenneth (2015). "Metaheuristics". Scholarpedia. 10 (4): 6532. doi:10.4249/scholarpedia.6532. ISSN 1941-6016.
- Birattari, Mauro; Paquete, Luis; Stützle, Thomas; Varrentrapp, Klaus (2001). "Classification of Metaheuristics and Design of Experiments for the Analysis of Components". S2CID 18347906.
- D, Binu (2019). "RideNN: A New Rider Optimization Algorithm-Based Neural Network for Fault Diagnosis in Analog Circuits". IEEE Transactions on Instrumentation and Measurement. 68 (1): 2–26. Bibcode:2019ITIM...68....2B. doi:10.1109/TIM.2018.2836058. S2CID 54459927.
- ^ Pang, Shinsiong; Chen, Mu-Chen (2023-06-01). "Optimize railway crew scheduling by using modified bacterial foraging algorithm". Computers & Industrial Engineering. 180: 109218. doi:10.1016/j.cie.2023.109218. ISSN 0360-8352. S2CID 257990456.
- ^ M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italie, 1992.
- ^ Moscato, P. (1989). "On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms". Caltech Concurrent Computation Program (report 826).
- Cantú-Paz, Erick (2001). Efficient and Accurate Parallel Genetic Algorithms. Genetic Algorithms and Evolutionary Computation. Vol. 1. Boston, MA: Springer US. doi:10.1007/978-1-4615-4369-5. ISBN 978-1-4613-6964-6.
- ^ Sudholt, Dirk (2015), Kacprzyk, Janusz; Pedrycz, Witold (eds.), "Parallel Evolutionary Algorithms", Springer Handbook of Computational Intelligence, Berlin, Heidelberg: Springer, pp. 929–959, doi:10.1007/978-3-662-43505-2_46, ISBN 978-3-662-43504-5, retrieved 2024-09-04
- ^ Khalloof, Hatem; Mohammad, Mohammad; Shahoud, Shadi; Duepmeier, Clemens; Hagenmeyer, Veit (2020-11-02), "A Generic Flexible and Scalable Framework for Hierarchical Parallelization of Population-Based Metaheuristics", Proc. of the 12th Int. Conf. on Management of Digital EcoSystems (MEDES'20), ACM, pp. 124–131, doi:10.1145/3415958.3433041, ISBN 978-1-4503-8115-4
- Swan, Jerry; Adriaensen, Steven; Bishr, Mohamed; Burke, Edmund K.; Clark, John A.; De Causmaecke, Patrick; Durillo, Juan José; Hammond, Kevin; Hart, Emma; Johnson, Colin G.; Kocsis, Zoltan A.; Kovitz, Ben; Krawiec, Krzysztof; Martin, Simon; Merelo, Juan J.; Minku, Leandro L.; Özcan, Ender; Pappa, Gisele Lobo; Pesch, Erwin; García-Sánchez, Pablo; Schaerf, Andrea; Sim, Kevin; Smith, Jim; Stützle, Thomas; Wagner, Stefan (2015). "A Research Agenda for Metaheuristic Standardization". Semantic Scholar. S2CID 63728283. Retrieved 2024-08-30.
- "Journal of Heuristic Policies on Heuristic Search Research" (PDF). Journal of Heuristics - Submission guidelines. Archived from the original on 2017-07-09. Retrieved 2024-09-01.
- "Aims and scope". 4OR. Retrieved 2024-09-01.
- "Aims and scope". Memetic Computing. Retrieved 2024-09-01.
- Almeida, Francisco; Blesa Aguilera, María J.; Blum, Christian; Moreno Vega, José Marcos; Pérez Pérez, Melquíades; Roli, Andrea; Sampels, Michael, eds. (2006). Hybrid Metaheuristics. Lecture Notes in Computer Science. Vol. 4030. Berlin, Heidelberg: Springer. doi:10.1007/11890584. ISBN 978-3-540-46384-9.
- Neri, Ferrante; Cotta, Carlos; Moscato, Pablo, eds. (2012). Handbook of Memetic Algorithms. Studies in Computational Intelligence. Vol. 379. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-23247-3. ISBN 978-3-642-23246-6.
- Dorigo, M.; Gambardella, L.M. (April 1997). "Ant colony system: a cooperative learning approach to the traveling salesman problem". IEEE Transactions on Evolutionary Computation. 1 (1): 53–66. doi:10.1109/4235.585892.
- Merz, Peter; Freisleben, Bernd (2002). "Memetic Algorithms for the Traveling Salesman Problem". Complex Systems. 13 (4).
- Tomoiagă B, Chindriş M, Sumper A, Sudria-Andreu A, Villafafila-Robles R. Pareto Optimal Reconfiguration of Power Distribution Systems Using a Genetic Algorithm Based on NSGA-II. Energies. 2013; 6(3):1439–1455.
- Ganesan, T.; Elamvazuthi, I.; Ku Shaari, Ku Zilati; Vasant, P. (2013-03-01). "Swarm intelligence and gravitational search algorithm for multi-objective optimization of synthesis gas production". Applied Energy. 103: 368–374. Bibcode:2013ApEn..103..368G. doi:10.1016/j.apenergy.2012.09.059.
- Ganesan, T.; Elamvazuthi, I.; Vasant, P. (2011-11-01). "Evolutionary normal-boundary intersection (ENBI) method for multi-objective optimization of green sand mould system". 2011 IEEE International Conference on Control System, Computing and Engineering. pp. 86–91. doi:10.1109/ICCSCE.2011.6190501. ISBN 978-1-4577-1642-3. S2CID 698459.
- Xhafa, Fatos; Abraham, Ajith, eds. (2008). Metaheuristics for Scheduling in Industrial and Manufacturing Applications. Studies in Computational Intelligence. Vol. 128. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-540-78985-7. ISBN 978-3-540-78984-0. S2CID 42238720.
- Jakob, Wilfried; Strack, Sylvia; Quinte, Alexander; Bengel, Günther; Stucky, Karl-Uwe; Süß, Wolfgang (2013-04-22). "Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing". Algorithms. 6 (2): 245–277. doi:10.3390/a6020245. ISSN 1999-4893.
- Kizilay, Damla; Tasgetiren, M. Fatih; Pan, Quan-Ke; Süer, Gürsel (2019). "An Ensemble of Meta-Heuristics for the Energy-Efficient Blocking Flowshop Scheduling Problem". Procedia Manufacturing. 39: 1177–1184. doi:10.1016/j.promfg.2020.01.352. S2CID 213710393.
- Grosch, Benedikt; Weitzel, Timm; Panten, Niklas; Abele, Eberhard (2019). "A metaheuristic for energy adaptive production scheduling with multiple energy carriers and its implementation in a real production system". Procedia CIRP. 80: 203–208. doi:10.1016/j.procir.2019.01.043. S2CID 164850023.
- ^ Holland, J.H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press. ISBN 978-0-262-08213-6.
- ^ Glover, Fred (1977). "Heuristics for Integer programming Using Surrogate Constraints". Decision Sciences. 8 (1): 156–166. CiteSeerX 10.1.1.302.4071. doi:10.1111/j.1540-5915.1977.tb01074.x.
- ^ Glover, F. (1986). "Future Paths for Integer Programming and Links to Artificial Intelligence". Computers and Operations Research. 13 (5): 533–549. doi:10.1016/0305-0548(86)90048-1.
- Quinte, Alexander; Jakob, Wilfried; Scherer, Klaus-Peter; Eggert, Horst (2002), Laudon, Matthew (ed.), "Optimization of a Micro Actuator Plate Using Evolutionary Algorithms and Simulation Based on Discrete Element Methods", International Conference on Modeling and Simulation of Microsystems: MSM 2002, Cambridge, Mass: Computational Publications, pp. 192–197, ISBN 978-0-9708275-7-9
- Parmee, I. C. (1997), Dasgupta, Dipankar; Michalewicz, Zbigniew (eds.), "Strategies for the Integration of Evolutionary/Adaptive Search with the Engineering Design Process", Evolutionary Algorithms in Engineering Applications, Berlin, Heidelberg: Springer, pp. 453–477, doi:10.1007/978-3-662-03423-1_25, ISBN 978-3-642-08282-5, retrieved 2023-07-17
- Valadi, Jayaraman; Siarry, Patrick, eds. (2014). Applications of Metaheuristics in Process Engineering. Cham: Springer International Publishing. doi:10.1007/978-3-319-06508-3. ISBN 978-3-319-06507-6. S2CID 40197553.
- Sanchez, Ernesto; Squillero, Giovanni; Tonda, Alberto (2012). Industrial Applications of Evolutionary Algorithms. Intelligent Systems Reference Library. Vol. 34. Berlin, Heidelberg: Springer. doi:10.1007/978-3-642-27467-1. ISBN 978-3-642-27466-4.
- Akan, Taymaz; Anter, Ahmed M.; Etaner-Uyar, A. Şima; Oliva, Diego, eds. (2023). Engineering Applications of Modern Metaheuristics. Studies in Computational Intelligence. Vol. 1069. Cham: Springer International Publishing. doi:10.1007/978-3-031-16832-1. ISBN 978-3-031-16831-4. S2CID 254222401.
- Blume, Christian (2000), Cagnoni, Stefano (ed.), "Optimized Collision Free Robot Move Statement Generation by the Evolutionary Software GLEAM", Real-World Applications of Evolutionary Computing, Lecture Notes in Computer Science, vol. 1803, Berlin, Heidelberg: Springer, pp. 330–341, doi:10.1007/3-540-45561-2_32, ISBN 978-3-540-67353-8, retrieved 2023-07-17
- Pholdee, Nantiwat; Bureerat, Sujin (2018-12-14), "Multiobjective Trajectory Planning of a 6D Robot based on Multiobjective Meta Heuristic Search", International Conference on Network, Communication and Computing (ICNCC 2018), ACM, pp. 352–356, doi:10.1145/3301326.3301356, ISBN 978-1-4503-6553-6, S2CID 77394395
- ^ Parejo, José Antonio; Ruiz-Cortés, Antonio; Lozano, Sebastián; Fernandez, Pablo (March 2012). "Metaheuristic optimization frameworks: a survey and benchmarking". Soft Computing. 16 (3): 527–561. doi:10.1007/s00500-011-0754-8. ISSN 1432-7643.
- García-Valdez, Mario; Merelo, J.J. (2017-07-15), "evospace-js: asynchronous pool-based execution of heterogeneous metaheuristics", GECCO '17: Proceedings of the Genetic and Evolutionary Computation Conference, Companion, New York: ACM, pp. 1202–1208, doi:10.1145/3067695.3082473, ISBN 978-1-4503-4939-0
- Lim, Dudy; Ong, Yew-Soon; Jin, Yaochu; Sendhoff, Bernhard; Lee, Bu-Sung (May 2007). "Efficient Hierarchical Parallel Genetic Algorithms using Grid computing". Future Generation Computer Systems. 23 (4): 658–670. doi:10.1016/j.future.2006.10.008.
- Nebro, Antonio J.; Barba-González, Cristóbal; Nieto, José García; Cordero, José A.; Montes, José F. Aldana (2017-07-15), "Design and architecture of the jMetaISP framework", GECCO '17: Proceedings of the Genetic and Evolutionary Computation Conference, Companion, New York: ACM, pp. 1239–1246, doi:10.1145/3067695.3082466, ISBN 978-1-4503-4939-0
- Robbins, H.; Monro, S. (1951). "A Stochastic Approximation Method" (PDF). Annals of Mathematical Statistics. 22 (3): 400–407. doi:10.1214/aoms/1177729586.
- Barricelli, N.A. (1954). "Esempi numerici di processi di evoluzione". Methodos: 45–68.
- Rastrigin, L.A. (1963). "The convergence of the random search method in the extremal control of a many parameter system". Automation and Remote Control. 24 (10): 1337–1342.
- Matyas, J. (1965). "Random optimization". Automation and Remote Control. 26 (2): 246–253.
- Nelder, J.A.; Mead, R. (1965). "A simplex method for function minimization". Computer Journal. 7 (4): 308–313. doi:10.1093/comjnl/7.4.308. S2CID 2208295.
- Rechenberg, Ingo (1965). "Cybernetic Solution Path of an Experimental Problem". Royal Aircraft Establishment, Library Translation.
- Fogel, L.; Owens, A.J.; Walsh, M.J. (1966). Artificial Intelligence through Simulated Evolution. Wiley. ISBN 978-0-471-26516-0.
- Hastings, W.K. (1970). "Monte Carlo Sampling Methods Using Markov Chains and Their Applications". Biometrika. 57 (1): 97–109. Bibcode:1970Bimka..57...97H. doi:10.1093/biomet/57.1.97. S2CID 21204149.
- Cavicchio, D.J. (1970). "Adaptive search using simulated evolution". Technical Report. University of Michigan, Computer and Communication Sciences Department. hdl:2027.42/4042.
- Kernighan, B.W.; Lin, S. (1970). "An efficient heuristic procedure for partitioning graphs". Bell System Technical Journal. 49 (2): 291–307. doi:10.1002/j.1538-7305.1970.tb01770.x.
- Mercer, R.E.; Sampson, J.R. (1978). "Adaptive search using a reproductive metaplan". Kybernetes. 7 (3): 215–228. doi:10.1108/eb005486.
- Smith, S.F. (1980). A Learning System Based on Genetic Adaptive Algorithms (PhD Thesis). University of Pittsburgh.
- Kirkpatrick, S.; Gelatt Jr., C.D.; Vecchi, M.P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. Bibcode:1983Sci...220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. PMID 17813860. S2CID 205939.
- Moscato, P.; Fontanari, J.F. (1990), "Stochastic versus deterministic update in simulated annealing", Physics Letters A, 146 (4): 204–208, Bibcode:1990PhLA..146..204M, doi:10.1016/0375-9601(90)90166-L
- Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, Bibcode:1990JCoPh..90..161D, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
- Wolpert, D.H.; Macready, W.G. (1995). "No free lunch theorems for search". Technical Report SFI-TR-95-02-010. Santa Fe Institute. S2CID 12890367.
- Igel, Christian, Toussaint, Marc (Jun 2003). "On classes of functions for which No Free Lunch results hold". Information Processing Letters. 86 (6): 317–321. arXiv:cs/0108011. doi:10.1016/S0020-0190(03)00222-9. ISSN 0020-0190. S2CID 147624.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Auger, Anne, Teytaud, Olivier (2010). "Continuous Lunches Are Free Plus the Design of Optimal Optimization Algorithms". Algorithmica. 57 (1): 121–146. CiteSeerX 10.1.1.186.6007. doi:10.1007/s00453-008-9244-5. ISSN 0178-4617. S2CID 1989533.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Stefan Droste; Thomas Jansen; Ingo Wegener (2002). "Optimization with Randomized Search Heuristics – The (A)NFL Theorem, Realistic Scenarios, and Difficult Functions". Theoretical Computer Science. 287 (1): 131–144. CiteSeerX 10.1.1.35.5850. doi:10.1016/s0304-3975(02)00094-4.
Further reading
- Sörensen, Kenneth; Sevaux, Marc; Glover, Fred (2017-01-16). "A History of Metaheuristics" (PDF). In Martí, Rafael; Panos, Pardalos; Resende, Mauricio (eds.). Handbook of Heuristics. Springer. ISBN 978-3-319-07123-7.
- Ashish Sharma (2022), Nature Inspired Algorithms with Randomized Hypercomputational Perspective. Information Sciences. https://doi.org/10.1016/j.ins.2022.05.020.
External links
- Fred Glover and Kenneth Sörensen (ed.). "Metaheuristics". Scholarpedia.
- EU/ME forum for researchers in the field.
- Metaheuristics.jl Source of some implementations.
| Optimization: Algorithms, methods, and heuristics | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|  | |||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||
| ||||||||||||||||||