Multiphoton intrapulse interference phase scan (MIIPS) is a method used in ultrashort laser technology that simultaneously measures (phase characterization), and compensates (phase correction) femtosecond laser pulses using an adaptive pulse shaper. When an ultrashort laser pulse reaches a duration of less than a few hundred femtosecond, it becomes critical to characterize its duration, its temporal intensity curve, or its electric field as a function of time. Classical photodetectors measuring the intensity of light are still too slow to allow for a direct measurement, even with the fastest photodiodes or streak cameras.
Other means have been developed based on quasi instantaneous non linear optical effects such as autocorrelation, FROG, SPIDER, etc. However, these can only measure the pulse characteristics but not correct for defects in order to make the pulse as short as possible. For instance, the pulse could be linearly chirped or present higher order group delay dispersion (GDD) so that its duration is longer than a bandwidth-limited pulse having the same intensity spectrum. It is therefore highly desirable to have a method which can not only characterize the pulse, but also correct the pulse to specific shapes for various applications in which repeatable pulse characteristics are requested. MIIPS can not only measure the pulse but also correct the high-order dispersion, thus is highly preferable for applications where repeatable electromagnetic field is important, such as to generate ultrashort pulses which are transform limited or possess specific phase characteristics.
The MIIPS method is also based on second-harmonic generation (SHG) in a non-linear crystal; however, instead of temporally scanning a replica of the pulse as in autocorrelation, a controllable and varying GDD is applied to the pulse through a pulse shaper. The intensity is maximal when the outgoing pulse is unchirped, or when the applied GDD exactly compensates the incoming pulse GDD. The pulse GDD is thus measured and compensated. By spectrally resolving the SHG signal, GDD can be measured as a function of frequency, so that the spectral phase can be measured and dispersion can be compensated to all orders.
Theory
A MIIPS-based device consists of two basic components controlled by a computer: a pulse shaper (usually a liquid crystal based spatial light modulator - SLM) and a spectrometer. The pulse shaper allows manipulation of the spectral phase and/or amplitude of the ultrashort pulses. The spectrometer records the spectrum of a nonlinear optical process such as second harmonic generation produced by the laser pulse. The MIIPS process is analogous to the Wheatstone bridge in electronics. A well-known (calibrated) spectral phase function is used in order to measure the unknown spectral phase distortions of the ultrashort laser pulses. Typically, the known superimposed function is a periodic sinusoidal function that is scanned across the bandwidth of the pulse.
MIIPS is similar to FROG in that a frequency trace is collected for the characterization of the ultrashort pulse. In Frequency-resolved optical gating, a FROG trace is collected through scanning the ultrashort pulse across the temporal axis, and detecting the spectrum of the nonlinear process. It can be expressed as
In MIIPS, instead of scanning on the temporal domain, a series of phase scan is applied on the phase domain of the pulse. The trace of the MIIPS scan consists of the second-harmonic spectra of each phase scan. The signal of MIIPS can be written as
The phase scan in MIIPS is realized with introducing a well-known reference function, , by the pulse shaper to locally cancel distortions by the unknown spectral phase, , of the pulse. The sum of the unknown phase and the reference phase is given by . Because the frequency doubled spectrum of the pulse depends on , it is possible to accurately retrieve the unknown .
The phase modulation procedure of the physical process is generally a continuous function. Thus, the SHG signal can be expanded with a Taylor expansion around :
And
According to this equation, the SHG signal reaches maximum when is zero. This is equivalent to . Through scanning of , the can be decided.
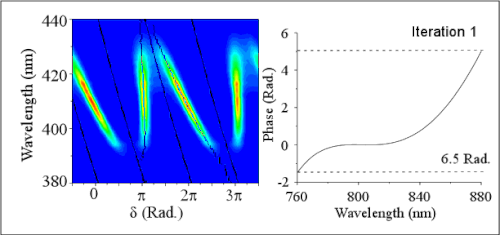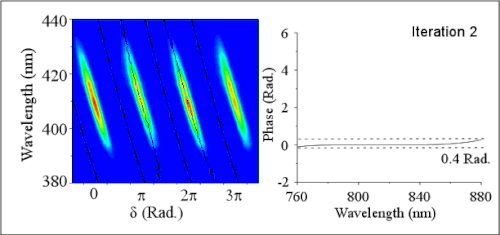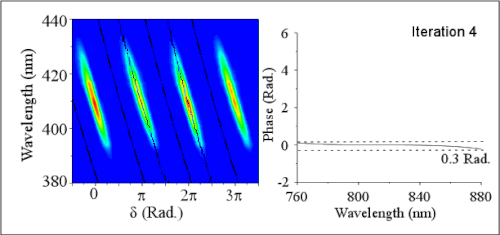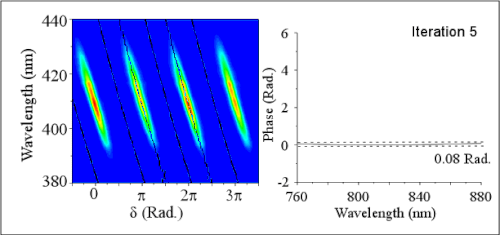
The frequency doubled spectrum recorded for each full scan of the reference phase results in two replicas of the MIIPS trace (see Figure 1, four replicas shown). From this data, a 2D plot for SHG() is constructed where . The second harmonic spectrum of the resulting pulse has a maximum amplitude at the frequency where the second derivative of the pulse has been compensated. The lines describing are used to obtain analytically the second derivative of the unknown phase. After double integration the phase distortions are known. The system then introduces a correction phase to cancel the distortions and achieve shorter pulses. The absolute accuracy of MIIPS improves as the phase distortions diminish, therefore an iterative procedure of measurement and compensation is applied to reduce phase distortions below 0.1 radian for all frequencies within the bandwidth of the laser.
When all phase distortions have been eliminated, the pulses have the highest possible peak power, and are considered to be Bandwidth-limited-pulse|transform limited (TL). The MIIPS trace corresponding to TL pulses shows straight parallel lines separated by . Once spectral phase distortions have been eliminated, the shaper can be used to introduce calibrated phases and amplitudes to control laser induced processes.
MIIPS technology has been applied successfully in selective excitation of multiphoton imaging and femtosecond light-mass interaction study.
Experimental setup

The expanded laser beam reaches the Diffractive grating (G) first, the first-order reflection is deflected to the Mirror (M) and then to the curved mirror (CM). The curved mirror reflects the laser to the spatial light modulator (SLM). The phases are applied through the SLM to each component of the frequency. The laser is then retro-reflected. By using a nonlinear medium, the nonlinear (SHG, THG, etc.) spectra vs. the phase scan can be recorded as a MIIPS trace for the characterization of the pulse. Once the pulse is characterized, a compensatory phase can be applied to the ultrashort pulse through the SLM.
Variants
There is also an improved MIIPS algorithm that allows for efficient phase retrieval in a single iteration, providing that the laser spectrum at the reference sample is known. This technique is expected to be particularly beneficial for measuring photosensitive samples, and it is also helpful in the case of samples which produce very low second harmonic spectra. This method of analysis avoids a type of non-trivial ambiguity that arises for structured amplitude pulse profiles and can provide better feedback on the accuracy of the phase retrieval.
Gated-MIIPS (G-MIIPS) is an enhanced variant of MIIPS, designed to address the limitations posed by higher-order phase distortions in ultrashort laser pulse characterization. G-MIIPS employs an amplitude gate scanned across the spectrum, mitigating the influence of higher-order phase terms and enabling efficient compression of broadband laser pulses with a simple 4𝑓 pulse shaper setup. G-MIIPS is particularly effective for correcting substantial phase distortions caused by factors like high-NA microscope objectives.
Other ultrashort pulse measurement techniques
- Frequency-resolved Optical Gating (FROG)
- Spectral phase interferometry for direct electric-field reconstruction (SPIDER)
References
- M. Dantus, V. V. Lozovoy, and I. Pastirk, "Measurement and Repair: The femtosecond Wheatstone Bridge." OE Magazine 9 (2003).
- V. V. Lozovoy, I. Pastirk, and M. Dantus, "Multiphoton intrapulse interference 4: Characterization and compensation of the spectral phase of ultrashort laser pulses." Optics Letters 29, 775-777 (2004).
- B. Xu, J. M. Gunn, J. M. Dela Cruz, V. V. Lozovoy, M. Dantus, “Quantitative investigation of the MIIPS method for phase measurement and compensation of femtosecond laser pulses,” J. Optical Society of America B 23, 750-759 (2006).
- A. Comin, R. Ciesielski, N. Coca-Lopez, A. Hartschuh, "Phase retrieval of ultrashort laser pulses using a MIIPS algorithm," Opt. Express 24, 2505-2512 (2016)
- A. Comin, R. Ciesielski, G. Piredda, K. Donkers, A. Hartschuh, "Compression of ultrashort laser pulses via gated multiphoton intrapulse interference phase scans," J. Opt. Soc. Am. B 31, 1118-1125 (2014)
References
- Comin, Alberto; Ciesielski, Richard; Coca-López, Nicolás; Hartschuh, Achim (8 February 2016). "Phase retrieval of ultrashort laser pulses using a MIIPS algorithm". Optics Express. 24 (3): 2505. doi:10.1364/OE.24.002505.
- Comin, Alberto; Ciesielski, Richard; Piredda, Giovanni; Donkers, Kevin; Hartschuh, Achim (1 May 2014). "Compression of ultrashort laser pulses via gated multiphoton intrapulse interference phase scans". Journal of the Optical Society of America B. 31 (5): 1118. arXiv:1401.5952. doi:10.1364/JOSAB.31.001118.


 , by the pulse shaper to locally cancel distortions by the unknown spectral phase,
, by the pulse shaper to locally cancel distortions by the unknown spectral phase,  , of the pulse. The sum of the unknown phase and the reference phase is given by
, of the pulse. The sum of the unknown phase and the reference phase is given by  . Because the frequency doubled spectrum of the pulse depends on
. Because the frequency doubled spectrum of the pulse depends on  , it is possible to accurately retrieve the unknown
, it is possible to accurately retrieve the unknown  :
:


 is zero. This is equivalent to
is zero. This is equivalent to  . Through scanning of
. Through scanning of  results in two replicas of the MIIPS trace (see Figure 1, four replicas shown). From this data, a 2D plot for SHG(
results in two replicas of the MIIPS trace (see Figure 1, four replicas shown). From this data, a 2D plot for SHG( ) is constructed where
) is constructed where  . The second harmonic spectrum of the resulting pulse has a maximum amplitude at the frequency where the second derivative of the pulse has been compensated. The lines describing
. The second harmonic spectrum of the resulting pulse has a maximum amplitude at the frequency where the second derivative of the pulse has been compensated. The lines describing  are used to obtain analytically the second derivative of the unknown phase. After double integration the phase distortions are known. The system then introduces a correction phase to cancel the distortions and achieve shorter pulses. The absolute accuracy of MIIPS improves as the phase distortions diminish, therefore an iterative procedure of measurement and compensation is applied to reduce phase distortions below 0.1 radian for all frequencies within the bandwidth of the laser.
are used to obtain analytically the second derivative of the unknown phase. After double integration the phase distortions are known. The system then introduces a correction phase to cancel the distortions and achieve shorter pulses. The absolute accuracy of MIIPS improves as the phase distortions diminish, therefore an iterative procedure of measurement and compensation is applied to reduce phase distortions below 0.1 radian for all frequencies within the bandwidth of the laser.
 . Once spectral phase distortions have been eliminated, the shaper can be used to introduce calibrated phases and amplitudes to control laser induced processes.
. Once spectral phase distortions have been eliminated, the shaper can be used to introduce calibrated phases and amplitudes to control laser induced processes.