In electrochemistry, the standard hydrogen electrode (abbreviated SHE), is a redox electrode which forms the basis of the thermodynamic scale of oxidation-reduction potentials. Its absolute electrode potential is estimated to be 4.44 ± 0.02 V at 25 °C, but to form a basis for comparison with all other electrochemical reactions, hydrogen's standard electrode potential (E°) is declared to be zero volts at any temperature. Potentials of all other electrodes are compared with that of the standard hydrogen electrode at the same temperature.
Nernst equation for SHE
See also: Nernst equation, Thermodynamic activity, and Standard stateThe hydrogen electrode is based on the redox half cell corresponding to the reduction of two hydrated protons, 2H(aq), into one gaseous hydrogen molecule, H2(g).
General equation for a reduction reaction:
The reaction quotient (Qr) of the half-reaction is the ratio between the chemical activities (a) of the reduced form (the reductant, ared) and the oxidized form (the oxidant, aox).
Considering the 2 H / H2 redox couple:
at chemical equilibrium, the ratio Qr of the reaction products by the reagents is equal to the equilibrium constant K of the half-reaction:
where
- and correspond to the chemical activities of the reduced and oxidized species involved in the redox reaction
- represents the activity of H
. - denotes the chemical activity of gaseous hydrogen (H
2), which is approximated here by its fugacity - denotes the partial pressure of gaseous hydrogen, expressed without unit; where
- is the H
2 mole fraction - is the total gas pressure in the system
- is the H
- p is the standard pressure (1 bar = 10 pascal) introduced here simply to overcome the pressure unit and to obtain an equilibrium constant without unit.
More details on managing gas fugacity to get rid of the pressure unit in thermodynamic calculations can be found at thermodynamic activity#Gases. The followed approach is the same as for chemical activity and molar concentration of solutes in solution. In the SHE, pure hydrogen gas () at the standard pressure of 1 bar is engaged in the system. Meanwhile the general SHE equation can also be applied to other thermodynamic systems with different mole fraction or total pressure of hydrogen.
This redox reaction occurs at a platinized platinum electrode. The electrode is immersed in the acidic solution and pure hydrogen gas is bubbled over its surface. The concentration of both the reduced and oxidised forms of hydrogen are maintained at unity. That implies that the pressure of hydrogen gas is 1 bar (100 kPa) and the activity coefficient of hydrogen ions in the solution is unity. The activity of hydrogen ions is their effective concentration, which is equal to the formal concentration times the activity coefficient. These unit-less activity coefficients are close to 1.00 for very dilute water solutions, but usually lower for more concentrated solutions.
As the general form of the Nernst equation at equilibrium is the following:
and as by definition in the case of the SHE,
The Nernst equation for the SHE becomes:
Simply neglecting the pressure unit present in , this last equation can often be directly written as:
And by solving the numerical values for the term
the practical formula commonly used in the calculations of this Nernst equation is:
- (unit: volt)
As under standard conditions the equation simplifies to:
- (unit: volt)
This last equation describes the straight line with a negative slope of -0.0591 volt/ pH unit delimiting the lower stability region of water in a Pourbaix diagram where gaseous hydrogen is evolving because of water decomposition.
where:
- is the activity of the hydrogen ions (H) in aqueous solution,
with:- is the activity coefficient of hydrogen ions (H) in aqueous solution
- is the molar concentration of hydrogen ions (H) in aqueous solution
- C is the standard concentration (1 M) used to overcome concentration unit
- is the partial pressure of the hydrogen gas, in bar (1 bar = 10 Pa)
- R is the universal gas constant: 8.3144 J⋅K⋅mol (rounded here to 4 decimal)
- T is the absolute temperature, in kelvin (at 25 °C: 298.15 K)
- F is the Faraday constant (the charge per mole of electrons), equal to 96,485.3 coulomb·mol
- p is the standard pressure: 1 bar = 10 Pa
Note: as the system is at chemical equilibrium, hydrogen gas, H2(g), is also in equilibrium with dissolved hydrogen, H2(aq), and the Nernst equation implicitly takes into account the Henry's law for gas dissolution. Therefore, there is no need to independently consider the gas dissolution process in the system, as it is already de facto included.
SHE vs NHE vs RHE
During the early development of electrochemistry, researchers used the normal hydrogen electrode as their standard for zero potential. This was convenient because it could actually be constructed by " a platinum electrode into a solution of 1 N strong acid and hydrogen gas through the solution at about 1 atm pressure". However, this electrode/solution interface was later changed. What replaced it was a theoretical electrode/solution interface, where the concentration of H was 1 M, but the H ions were assumed to have no interaction with other ions (a condition not physically attainable at those concentrations). To differentiate this new standard from the previous one, it was given the name 'standard hydrogen electrode'. Finally, there are also reversible hydrogen electrodes (RHEs), which are practical hydrogen electrodes whose potential depends on the pH of the solution.
In summary,
- NHE (normal hydrogen electrode): potential of a platinum electrode in 1 M acid solution with 1 bar of hydrogen bubbled through
- SHE (standard hydrogen electrode): potential of a platinum electrode in a theoretical ideal solution (the current standard for zero potential for all temperatures)
- RHE (reversible hydrogen electrode): a practical hydrogen electrode whose potential depends on the pH of the solution
Choice of platinum
The choice of platinum for the hydrogen electrode is due to several factors:
- inertness of platinum (it does not corrode)
- the capability of platinum to catalyze the reaction of proton reduction
- a high intrinsic exchange current density for proton reduction on platinum
- excellent reproducibility of the potential (bias of less than 10 μV when two well-made hydrogen electrodes are compared with one another)
The surface of platinum is platinized (i.e., covered with a layer of fine powdered platinum also known as platinum black) to:
- Increase total surface area. This improves reaction kinetics and maximum possible current
- Use a surface material that adsorbs hydrogen well at its interface. This also improves reaction kinetics
Other metals can be used for fabricating electrodes with a similar function such as the palladium-hydrogen electrode.
Interference
Because of the high adsorption activity of the platinized platinum electrode, it's very important to protect electrode surface and solution from the presence of organic substances as well as from atmospheric oxygen. Inorganic ions that can be reduced to a lower valency state at the electrode also have to be avoided (e.g., Fe
, CrO
4). A number of organic substances are also reduced by hydrogen on a platinum surface, and these also have to be avoided.
Cations that can be reduced and deposited on the platinum can be source of interference: silver, mercury, copper, lead, cadmium and thallium.
Substances that can inactivate ("poison") the catalytic sites include arsenic, sulfides and other sulfur compounds, colloidal substances, alkaloids, and material found in biological systems.
Isotopic effect
The standard redox potential of the deuterium couple is slightly different from that of the proton couple (ca. −0.0044 V vs SHE). Various values in this range have been obtained: −0.0061 V, −0.00431 V, −0.0074 V.
Also difference occurs when hydrogen deuteride (HD, or deuterated hydrogen, DH) is used instead of hydrogen in the electrode.
Experimental setup
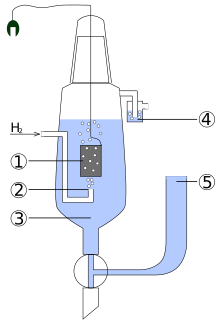
The scheme of the standard hydrogen electrode:
- platinized platinum electrode
- hydrogen gas
- solution of the acid with activity of H = 1 mol dm
- hydroseal for preventing oxygen interference
- reservoir through which the second half-element of the galvanic cell should be attached. The connection can be direct, through a narrow tube to reduce mixing, or through a salt bridge, depending on the other electrode and solution. This creates an ionically conductive path to the working electrode of interest.
See also
- Table of standard electrode potentials
- Reversible hydrogen electrode
- Palladium-hydrogen electrode
- Reference electrode
- Dynamic hydrogen electrode
- Quinhydrone electrode
- Thermodynamic activity
- Standard state
References
- Sergio Trasatti, "The Absolute Electrode Potential: an Explanatory Note (Recommendations 1986)", International Union of Pure and Applied Chemistry, Pure & AppL Chem., Vol. 58, No. 7, pp. 955–66, 1986. http://www.iupac.org/publications/pac/1986/pdf/5807x0955.pdf (pdf)
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "standard hydrogen electrode". doi:10.1351/goldbook.S05917
- Ramette, R. W. (October 1987). "Outmoded terminology: The normal hydrogen electrode". Journal of Chemical Education. 64 (10): 885. Bibcode:1987JChEd..64..885R. doi:10.1021/ed064p885.
- https://www.researchgate.net/post/Can_anyone_please_explain_me_the_difference_between_NHE_RHE_and_SHE_in_a_simple_way
- Sawyer, D. T.; Sobkowiak, A.; Roberts, J. L. Jr. (1995). Electrochemistry for Chemists (2nd ed.). John Wiley and Sons.
- Ives, D. J. G.; Janz, G. J. (1961). Reference Electrodes: Theory and Practice. Academic Press.
- Znamirovschi, V. (January 1970). "Isotopic Equilibrium at the Normal Hydrogen Electrode". Isotopenpraxis Isotopes in Environmental and Health Studies. 6 (1): 29–31. Bibcode:1970IIEHS...6...29Z. doi:10.1080/10256017008621700.
- Gary, Robert; Bates, Roger G.; Robinson, R. A. (May 1964). "Thermodynamics of Solutions of Deuterium Chloride in Heavy Water from 5 to 50°". The Journal of Physical Chemistry. 68 (5): 1186–1190. doi:10.1021/j100787a037.
- Wakao, S.; Yonemura, Y. (February 1983). "Anodic polarization behaviour of hydride-deuteride electrodes". Journal of the Less Common Metals. 89 (2): 481–488. doi:10.1016/0022-5088(83)90359-4.
External links
- Palibroda, Evelina (January 1967). "Note sur l'activation anodique de la surface du métal support de l'électrode à hydrogène". Journal of Electroanalytical Chemistry and Interfacial Electrochemistry. 15: 92–95. doi:10.1016/0022-0728(67)85013-7.




 and
and  correspond to the
correspond to the  represents the activity of H
represents the activity of H denotes the chemical activity of gaseous hydrogen (H
denotes the chemical activity of gaseous hydrogen (H
 denotes the
denotes the  where
where
 is the H
is the H is the total gas pressure in the system
is the total gas pressure in the system ) at the standard pressure
) at the standard pressure 
 by definition in the case of the SHE,
by definition in the case of the SHE,




 (unit:
(unit: 
 the equation simplifies to:
the equation simplifies to:
 (unit:
(unit: 
 is the
is the  is the
is the 