24-cell |
 Runcinated 24-cell |
 Runcitruncated 24-cell |
 Omnitruncated 24-cell (Runcicantitruncated 24-cell) |
| Orthogonal projections in F4 Coxeter plane | |
|---|---|
In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination (a 3rd order truncation) of the regular 24-cell.
There are 3 unique degrees of runcinations of the 24-cell including with permutations truncations and cantellations.
Runcinated 24-cell
| Runcinated 24-cell | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | t0,3{3,4,3} | |
| Coxeter diagram | ||
| Cells | 240 | 48 3.3.3.3 192 3.4.4 |
| Faces | 672 | 384{3} 288{4} |
| Edges | 576 | |
| Vertices | 144 | |
| Vertex figure |  elongated square antiprism | |
| Symmetry group | Aut(F4), ], order 2304 | |
| Properties | convex, edge-transitive | |
| Uniform index | 25 26 27 | |

In geometry, the runcinated 24-cell or small prismatotetracontoctachoron is a uniform 4-polytope bounded by 48 octahedra and 192 triangular prisms. The octahedral cells correspond with the cells of a 24-cell and its dual.
E. L. Elte identified it in 1912 as a semiregular polytope.
Alternate names
- Runcinated 24-cell (Norman W. Johnson)
- Runcinated icositetrachoron
- Runcinated polyoctahedron
- Small prismatotetracontoctachoron (spic) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the runcinated 24-cell having edge length 2 is given by all permutations of sign and coordinates of:
- (0, 0, √2, 2+√2)
- (1, 1, 1+√2, 1+√2)
The permutations of the second set of coordinates coincide with the vertices of an inscribed cantellated tesseract.
Projections
| Coxeter plane | F4 | B4 |
|---|---|---|
| Graph | 
|

|
| Dihedral symmetry | ] = | |
| Coxeter plane | B3 / A2 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | ] = |
| 3D perspective projections | ||
|---|---|---|
 Schlegel diagram, centered on octahedron, with the octahedra shown. |
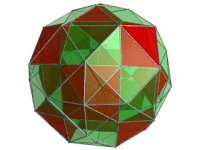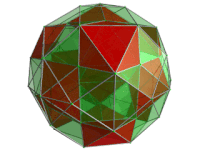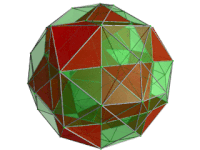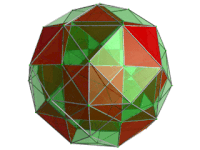 Perspective projection of the runcinated 24-cell into 3 dimensions, centered on an octahedral cell. The rotation is only of the 3D image, in order to show its structure, not a rotation in 4-space. Fifteen of the octahedral cells facing the 4D viewpoint are shown here in red. The gaps between them are filled up by a framework of triangular prisms. |
 Stereographic projection with 24 of its 48 octahedral cells |
Related regular skew polyhedron
The regular skew polyhedron, {4,8|3}, exists in 4-space with 8 square around each vertex, in a zig-zagging nonplanar vertex figure. These square faces can be seen on the runcinated 24-cell, using all 576 edges and 288 vertices. The 384 triangular faces of the runcinated 24-cell can be seen as removed. The dual regular skew polyhedron, {8,4|3}, is similarly related to the octagonal faces of the bitruncated 24-cell.
Runcitruncated 24-cell
| Runcitruncated 24-cell | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | t0,1,3{3,4,3} s2,3{3,4,3} | |
| Coxeter diagram | ||
| Cells | 240 | 24 4.6.6 96 4.4.6 96 3.4.4 24 3.4.4.4 |
| Faces | 1104 | 192{3} 720{4} 192{6} |
| Edges | 1440 | |
| Vertices | 576 | |
| Vertex figure |  Trapezoidal pyramid | |
| Symmetry group | F4, , order 1152 | |
| Properties | convex | |
| Uniform index | 28 29 30 | |

The runcitruncated 24-cell or prismatorhombated icositetrachoron is a uniform 4-polytope derived from the 24-cell. It is bounded by 24 truncated octahedra, corresponding with the cells of a 24-cell, 24 rhombicuboctahedra, corresponding with the cells of the dual 24-cell, 96 triangular prisms, and 96 hexagonal prisms.
Coordinates
The Cartesian coordinates of an origin-centered runcitruncated 24-cell having edge length 2 are given by all permutations of coordinates and sign of:
- (0, √2, 2√2, 2+3√2)
- (1, 1+√2, 1+2√2, 1+3√2)
The permutations of the second set of coordinates give the vertices of an inscribed omnitruncated tesseract.
The dual configuration has coordinates generated from all permutations and signs of:
- (1,1,1+√2,5+√2)
- (1,3,3+√2,3+√2)
- (2,2,2+√2,4+√2)
Projections
| Coxeter plane | F4 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 
|

|
| Dihedral symmetry | ||
| Coxeter plane | B4 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | ||
 Schlegel diagram centered on rhombicuboctahedron only triangular prisms shown |
Runcicantic snub 24-cell
A half-symmetry construction of the runcitruncated 24-cell (or runcicantellated 24-cell), as ![]()
![]()
![]()
![]()
![]()
![]()
![]() , also called a runcicantic snub 24-cell, as
, also called a runcicantic snub 24-cell, as ![]()
![]()
![]()
![]()
![]()
![]()
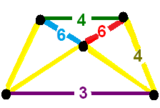
![]() , has an identical geometry, but its triangular faces are further subdivided. Like the snub 24-cell, it has symmetry , order 576. The runcitruncated 24-cell has 192 identical hexagonal faces, while the runcicantic snub 24-cell has 2 constructive sets of 96 hexagons.
The difference can be seen in the vertex figures:
, has an identical geometry, but its triangular faces are further subdivided. Like the snub 24-cell, it has symmetry , order 576. The runcitruncated 24-cell has 192 identical hexagonal faces, while the runcicantic snub 24-cell has 2 constructive sets of 96 hexagons.
The difference can be seen in the vertex figures:
 |
 |
Runcic snub 24-cell
| Runcic snub 24-cell | ||
|---|---|---|
| Schläfli symbol | s3{3,4,3} | |
| Coxeter diagram | ||
| Cells | 240 | 24 {3,5} 24 t{3,3} 96 (4.4.3) 96 tricup |
| Faces | 960 | 576 {3} 288 {4} 96 {6} |
| Edges | 1008 | |
| Vertices | 288 | |
| Vertex figure | 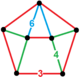
| |
| Symmetry group | , order 576 | |
| Properties | convex | |
A related 4-polytope is the runcic snub 24-cell or prismatorhombisnub icositetrachoron, s3{3,4,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is not uniform, but it is vertex-transitive and has all regular polygon faces. It is constructed with 24 icosahedra, 24 truncated tetrahedra, 96 triangular prisms, and 96 triangular cupolae in the gaps, for a total of 240 cells, 960 faces, 1008 edges, and 288 vertices. Like the snub 24-cell, it has symmetry , order 576.
. It is not uniform, but it is vertex-transitive and has all regular polygon faces. It is constructed with 24 icosahedra, 24 truncated tetrahedra, 96 triangular prisms, and 96 triangular cupolae in the gaps, for a total of 240 cells, 960 faces, 1008 edges, and 288 vertices. Like the snub 24-cell, it has symmetry , order 576.
The vertex figure contains one icosahedron, two triangular prisms, one truncated tetrahedron, and 3 triangular cupolae.
| Orthographic projections | Net | ||
|---|---|---|---|

|

|

|

|
Omnitruncated 24-cell
| Omnitruncated 24-cell | ||
| Type | Uniform 4-polytope | |
| Schläfli symbol | t0,1,2,3{3,4,3} | |
| Coxeter diagram | ||
| Cells | 240 | 48 (4.6.8) 192 (4.4.6) |
| Faces | 1392 | 864 {4} 384 {6} 144 {8} |
| Edges | 2304 | |
| Vertices | 1152 | |
| Vertex figure |  Phyllic disphenoid | |
| Symmetry group | Aut(F4), ], order 2304 | |
| Properties | convex | |
| Uniform index | 29 30 31 | |
The omnitruncated 24-cell or great prismatotetracontoctachoron is a uniform 4-polytope derived from the 24-cell. It is composed of 1152 vertices, 2304 edges, and 1392 faces (864 squares, 384 hexagons, and 144 octagons). It has 240 cells: 48 truncated cuboctahedra, 192 hexagonal prisms. Each vertex contains four cells in a phyllic disphenoidal vertex figure: two hexagonal prisms, and two truncated cuboctahedra.
Structure
The 48 truncated cuboctahedral cells are joined to each other via their octagonal faces. They can be grouped into two groups of 24 each, corresponding with the cells of a 24-cell and its dual. The gaps between them are filled in by a network of 192 hexagonal prisms, joined to each other via alternating square faces in alternating orientation, and to the truncated cuboctahedra via their hexagonal faces and remaining square faces.
Coordinates
The Cartesian coordinates of an omnitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:
- (1, 1+√2, 1+2√2, 5+3√2)
- (1, 3+√2, 3+2√2, 3+3√2)
- (2, 2+√2, 2+2√2, 4+3√2)
Images
| Coxeter plane | F4 | B4 |
|---|---|---|
| Graph | 
|
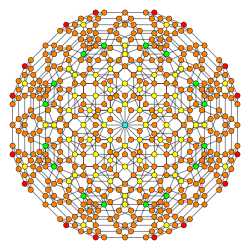
|
| Dihedral symmetry | ] = | |
| Coxeter plane | B3 / A2 | B2 / A3 |
| Graph | 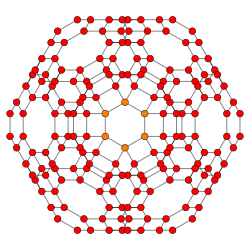
|

|
| Dihedral symmetry | ] = |
| 3D perspective projections | |
|---|---|
 Schlegel diagram |
 Perspective projection into 3D centered on a truncated cuboctahedron. The nearest great rhombicuboctahedral cell to the 4D viewpoint is shown in red, with the six surrounding great rhombicuboctahedra in yellow. Twelve of the hexagonal prisms sharing a square face with the nearest cell and hexagonal faces with the yellow cells are shown in blue. The remaining cells are shown in green. Cells lying on the far side of the polytope from the 4D viewpoint have been culled for clarity. |
 Omnitruncated 24-cell |
 Dual to omnitruncated 24-cell |
Related polytopes
Nonuniform variants with symmetry and two types of truncated cuboctahedra can be doubled by placing the two types of truncated cuboctahedra on each other to produce a nonuniform polychoron with 48 truncated cuboctahedra, 144 octagonal prisms (as ditetragonal trapezoprisms), 192 hexagonal prisms, two kinds of 864 rectangular trapezoprisms (288 with D2d symmetry and 576 with C2v symmetry), and 2304 vertices. Its vertex figure is an irregular triangular bipyramid.
This polychoron can then be alternated to produce another nonuniform polychoron with 48 snub cubes, 144 square antiprisms, 192 octahedra (as triangular antiprisms), three kinds of 2016 tetrahedra (288 tetragonal disphenoids, 576 phyllic disphenoids, and 1152 irregular tetrahedra), and 1152 vertices. It has a symmetry of ], order 1152.
Full snub 24-cell

The uniform snub 24-cell is called a semi-snub 24-cell by John Horton Conway with Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() within the F4 family, although it is a full snub or omnisnub within the D4 family, as
within the F4 family, although it is a full snub or omnisnub within the D4 family, as ![]()
![]()
![]()
![]()
![]() .
.
In contrast a full snub 24-cell or omnisnub 24-cell, defined as an alternation of the omnitruncated 24-cell, cannot be made uniform, but it can be given Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , and symmetry ], order 1152, and constructed from 48 snub cubes, 192 octahedrons, and 576 tetrahedrons filling the gaps at the deleted vertices. Its vertex figure contains 4 tetrahedra, 2 octahedra, and 2 snub cubes. It has 816 cells, 2832 faces, 2592 edges, and 576 vertices.
, and symmetry ], order 1152, and constructed from 48 snub cubes, 192 octahedrons, and 576 tetrahedrons filling the gaps at the deleted vertices. Its vertex figure contains 4 tetrahedra, 2 octahedra, and 2 snub cubes. It has 816 cells, 2832 faces, 2592 edges, and 576 vertices.
Related polytopes
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
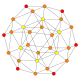
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
| Schlegel diagram |

|

|

|

|

|

|

|

|

|

| |
| F4 | 
|

|

|

|

|

|

|

|

|

| |
| B4 | 
|

|

|

|
|

|

|

|

|

| |
| B3(a) | 
|

|
|

|

|

|

|

|
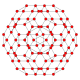
|

| |
| B3(b) | 
|
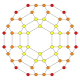
|

|
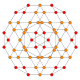
|

|
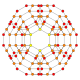
| |||||
| B2 | 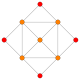
|

|

|

|

|

|

|
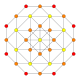
|
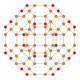
|

| |
Notes
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 and 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation m58 m59 m53
- 3. Convex uniform polychora based on the icositetrachoron (24-cell), George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora)". x3o4o3x - spic, x3x4o3x - prico, s3s4o3x - prissi, x3x4x3x - gippic
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||