
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary (i.e., non-oriented) matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
All oriented matroids have an underlying matroid. Thus, results on ordinary matroids can be applied to oriented matroids. However, the converse is false; some matroids cannot become an oriented matroid by orienting an underlying structure (e.g., circuits or independent sets). The distinction between matroids and oriented matroids is discussed further below.
Matroids are often useful in areas such as dimension theory and algorithms. Because of an oriented matroid's inclusion of additional details about the oriented nature of a structure, its usefulness extends further into several areas including geometry and optimization.
History
The first appearance of oriented matroids was in a 1966 article by George J. Minty and was confined to regular matroids.
Subsequently R.T. Rockefellar (1969) suggested the problem of generalizing Minty's concept to real vector spaces. His proposal helped lead to the development of the general theory.
Background
Main article: Signed setIn order to abstract the concept of orientation on the edges of a graph to sets, one needs the ability to assign "direction" to the elements of a set. The way this achieved is with the following definition of signed sets.
- A signed set, , combines a set of objects, , with an ordered bipartition of that set into two disjoint subsets: and .
- The members of are called the positive elements; members of are the negative elements.
- The set is called the support of .
- The empty signed set, , is defined as the empty set combined with an (ordered) bipartition of it into two empty sets: and .
- The signed set is the opposite of , written , if and
Given an element of the support, we will write for a positive element and for a negative element. In this way, a signed set is just adding negative signs to distinguished elements. This will make sense as a "direction" only when we consider orientations of larger structures. Then the sign of each element will encode its direction relative to this orientation.
Axiomatizations
See also: Matroid § Bases and circuits, Axiomatic system, and CryptomorphismLike ordinary matroids, several equivalent systems of axioms exist. (Such structures that possess multiple equivalent axiomatizations are called cryptomorphic.)
Circuit axioms
Let be any set. We refer to as the ground set. Let be a collection of signed sets, each of which is supported by a subset of . If the following axioms hold for , then equivalently is the set of signed circuits for an oriented matroid on .
- (C0)
- (C1) (symmetric)
- (C2) (incomparable)
- (C3) (weak elimination)
Vector Axioms
The composition of signed sets and is the signed set defined by , , and . The vectors of an oriented matroid are the compositions of circuits. The vectors of an oriented matroid satisfy the following axioms:
- for all ,
- for all , and , there is a , such that
- ,
- , and
- .
The covectors of an oriented matroid are the vectors of its dual oriented matroid.
Chirotope axioms
Let be as above. For each non-negative integer , a chirotope of rank is a function that satisfies the following axioms:
- (B0) (non-trivial): is not identically zero
- (B1) (alternating): For any permutation and , , where is the sign of the permutation.
- (B2) (exchange): For any such that for each , then we also have .
The term chirotope is derived from the mathematical notion of chirality, which is a concept abstracted from chemistry, where it is used to distinguish molecules that have the same structure except for a reflection.
Equivalence
Every chirotope of rank gives rise to a set of bases of a matroid on consisting of those -element subsets that assigns a nonzero value. The chirotope can then sign the circuits of that matroid. If is a circuit of the described matroid, then where is a basis. Then can be signed with positive elements
and negative elements the complement. Thus a chirotope gives rise to the oriented bases of an oriented matroid. In this sense, (B0) is the nonempty axiom for bases and (B2) is the basis exchange property.
Examples
Oriented matroids are often introduced (e.g., Bachem and Kern) as an abstraction for directed graphs or systems of linear inequalities. Below are the explicit constructions.
Directed graphs
Main article: Directed graph See also: Flow networkGiven a digraph, we define a signed circuit from the standard circuit of the graph by the following method. The support of the signed circuit is the standard set of edges in a minimal cycle. We go along the cycle in the clockwise or anticlockwise direction assigning those edges whose orientation agrees with the direction to the positive elements and those edges whose orientation disagrees with the direction to the negative elements . If is the set of all such , then is the set of signed circuits of an oriented matroid on the set of edges of the directed graph.
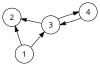
If we consider the directed graph on the right, then we can see that there are only two circuits, namely and . Then there are only four possible signed circuits corresponding to clockwise and anticlockwise orientations, namely , , , and . These four sets form the set of signed circuits of an oriented matroid on the set .
Linear algebra
See also: Matroid § Matroids from linear algebraIf is any finite subset of , then the set of minimal linearly dependent sets forms the circuit set of a matroid on . To extend this construction to oriented matroids, for each circuit there is a minimal linear dependence
with . Then the signed circuit has positive elements and negative elements . The set of all such forms the set of signed circuits of an oriented matroid on . Oriented matroids that can be realized this way are called representable.
Given the same set of vectors , we can define the same oriented matroid with a chirotope . For any let
where the right hand side of the equation is the sign of the determinant. Then is the chirotope of the same oriented matroid on the set .
Hyperplane arrangements
Main article: Arrangement of hyperplanesA real hyperplane arrangement is a finite set of hyperplanes in , each containing the origin. By picking one side of each hyperplane to be the positive side, we obtain an arrangement of half-spaces. A half-space arrangement breaks down the ambient space into a finite collection of cells, each defined by which side of each hyperplane it lands on. That is, assign each point to the signed set with if is on the positive side of and if is on the negative side of . This collection of signed sets defines the set of covectors of the oriented matroid, which are the vectors of the dual oriented matroid.
Convex polytope
Main article: Convex polytopeGünter M. Ziegler introduces oriented matroids via convex polytopes.
Results
Orientability
A standard matroid is called orientable if its circuits are the supports of signed circuits of some oriented matroid. It is known that all real representable matroids are orientable. It is also known that the class of orientable matroids is closed under taking minors, however the list of forbidden minors for orientable matroids is known to be infinite. In this sense, oriented matroids is a much stricter formalization than regular matroids.
Duality
See also: Matroid § DualityJust as a matroid has a unique duals, an oriented matroid has a unique dual, often called its "orthogonal dual". What this means is that the underlying matroids are dual and that the cocircuits are signed so that they are "orthogonal" to every circuit. Two signed sets are said to be orthogonal if the intersection of their supports is empty or if the restriction of their positive elements to the intersection and negative elements to the intersection form two nonidentical and non-opposite signed sets. The existence and uniqueness of the dual oriented matroid depends on the fact that every signed circuit is orthogonal to every signed cocircuit.
To see why orthogonality is necessary for uniqueness one needs only to look to the digraph example above. We know that for planar graphs the dual of the circuit matroid is the circuit matroid of the graph's planar dual. Thus there are as many different dual pairs of oriented matroids based on the matroid of the graph as there are ways to orient the graph and in a corresponding way its dual.
To see the explicit construction of this unique orthogonal dual oriented matroid, consider an oriented matroid's chirotope . If we consider a list of elements of as a cyclic permutation then we define to be the sign of the associated permutation. If is defined as
then is the chirotope of the unique orthogonal dual oriented matroid.
Topological representation

Not all oriented matroids are representable—that is, not all have realizations as point configurations, or, equivalently, hyperplane arrangements. However, in some sense, all oriented matroids come close to having realizations as hyperplane arrangements. In particular, the Folkman–Lawrence topological representation theorem states that any oriented matroid has a realization as an arrangement of pseudospheres. A -dimensional pseudosphere is an embedding of such that there exists a homeomorphism so that embeds as an equator of . In this sense a pseudosphere is just a tame sphere (as opposed to wild spheres). A pseudosphere arrangement in is a collection of pseudospheres that intersect along pseudospheres. Finally, the Folkman–Lawrence topological representation theorem states that every oriented matroid of rank can be obtained from a pseudosphere arrangement in . It is named after Jon Folkman and Jim Lawrence, who published it in 1978.
Geometry

The theory of oriented matroids has influenced the development of combinatorial geometry, especially the theory of convex polytopes, zonotopes, and configurations of vectors (equivalently, arrangements of hyperplanes). Many results—Carathéodory's theorem, Helly's theorem, Radon's theorem, the Hahn–Banach theorem, the Krein–Milman theorem, the lemma of Farkas—can be formulated using appropriate oriented matroids.
Optimization
The development of an axiom system for oriented matroids was initiated by R. Tyrrell Rockafellar to describe the sign patterns of the matrices arising through the pivoting operations of Dantzig's simplex algorithm; Rockafellar was inspired by Albert W. Tucker's studies of such sign patterns in "Tucker tableaux".
The theory of oriented matroids has led to breakthroughs in combinatorial optimization. In linear programming, it was the language in which Robert G. Bland formulated his pivoting rule, by which the simplex algorithm avoids cycles. Similarly, it was used by Terlaky and Zhang to prove that their criss-cross algorithms have finite termination for linear programming problems. Similar results were made in convex quadratic programming by Todd and Terlaky. It has been applied to linear-fractional programming, quadratic-programming problems, and linear complementarity problems.
Outside of combinatorial optimization, oriented matroid theory also appears in convex minimization in Rockafellar's theory of "monotropic programming" and related notions of "fortified descent". Similarly, matroid theory has influenced the development of combinatorial algorithms, particularly the greedy algorithm. More generally, a greedoid is useful for studying the finite termination of algorithms.
References
- R. Tyrrell Rockafellar 1969. Anders Björner et alia, Chapters 1-3. Jürgen Bokowski, Chapter 1. Günter M. Ziegler, Chapter 7.
- Björner et alia, Chapters 1-3. Bokowski, Chapters 1-4.
- Because matroids and oriented matroids are abstractions of other mathematical abstractions, nearly all the relevant books are written for mathematical scientists rather than for the general public. For learning about oriented matroids, a good preparation is to study the textbook on linear optimization by Nering and Tucker, which is infused with oriented-matroid ideas, and then to proceed to Ziegler's lectures on polytopes.
- Björner et alia, Chapter 7.9.
- G. J. Minty (1966), On the axiomatic foundations of the theories of directed linear graphs, electrical networks, and network programming. J. Math. Mech. 15: 485–520. Reprinted in D. R. Fulkerson, ed., Graph Theory, M.A.A. Study No. 12, Mathematical Association of America.
- Björner et alia, Chapter 3.5
- * Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). Oriented Matroids. Encyclopedia of Mathematics and Its Applications. Vol. 46 (2nd ed.). Cambridge University Press. ISBN 978-0-521-77750-6. OCLC 776950824. Zbl 0944.52006.
- Björner et alia, Chapter 7.9
- Björner et alia, Chapter 3.4
- Björner et alia, Chapter 3.6
- Björner et alia, Chapter 5.2
- Bachem and Kern, Chapters 1–2 and 4–9. Björner et alia, Chapters 1–8. Ziegler, Chapter 7–8. Bokowski, Chapters 7–10.
- Bachem and Wanka, Chapters 1–2, 5, 7–9. Björner et alia, Chapter 8.
- Rockafellar, R. Tyrrell (1969). "The elementary vectors of a subspace of (1967)" (PDF). In R. C. Bose; Thomas A. Dowling (eds.). Combinatorial Mathematics and its Applications. The University of North Carolina Monograph Series in Probability and Statistics. Chapel Hill, North Carolina: University of North Carolina Press. pp. 104–127. MR 0278972.
- Björner et alia, Chapters 8–9. Fukuda and Terlaky. Compare Ziegler.
- Illés, Szirmai & Terlaky (1999)
- Fukuda & Terlaky (1997)
- Fukuda & Terlaky (1997, p. 385)
- Fukuda & Namiki (1994, p. 367)
- Rockafellar 1984 and 1998.
- Lawler. Rockafellar 1984 and 1998.
Further reading
Books
- Bachem, Achim; Kern, Walter (1992). Linear Programming Duality: An Introduction to Oriented Matroids. Universitext. Springer-Verlag. doi:10.1007/978-3-642-58152-6. ISBN 978-3-540-55417-2. MR 1230380.
- Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). Oriented Matroids. Encyclopedia of Mathematics and Its Applications. Vol. 46 (2nd ed.). Cambridge University Press. ISBN 978-0-521-77750-6. Zbl 0944.52006.
- Bokowski, Jürgen (2006). Computational oriented matroids. Equivalence classes of matrices within a natural framework. Cambridge University Press. ISBN 978-0-521-84930-2. Zbl 1120.52011.
- Lawler, Eugene (2001). Combinatorial Optimization: Networks and Matroids. Dover. ISBN 978-0-486-41453-9. Zbl 1058.90057.
- Evar D. Nering and Albert W. Tucker, 1993, Linear Programs and Related Problems, Academic Press. (elementary)
- Rockafellar, R. Tyrrell (1984). Network Flows and Monotropic Optimization. Wiley-Interscience. republished by Athena Scientific of Dimitri Bertsekas, 1998.
- Ziegler, Günter M. (1994). Lectures on Polytopes. New York: Springer-Verlag.
- Richter-Gebert, Jürgen; Ziegler, Günter M. (1997). "Oriented Matroids". In Goodman, Jacob E.; O'Rourke, Joseph (eds.). Handbook of Discrete and Computational Geometry. Boca Raton: CRC Press. pp. 111–132. ISBN 9780849385247.
Articles
- A. Bachem, A. Wanka, Separation theorems for oriented matroids, Discrete Math. 70 (1988) 303–310.
- Bland, Robert G. (1977). "New finite pivoting rules for the simplex method". Mathematics of Operations Research. 2 (2): 103–107. doi:10.1287/moor.2.2.103.
- Folkman, Jon; Lawrence, Jim (October 1978). "Oriented Matroids". Journal of Combinatorial Theory. Series B. 25 (2): 199–236. doi:10.1016/0095-8956(78)90039-4.
- Fukuda, Komei; Terlaky, Tamás (1997). Thomas M. Liebling; Dominique de Werra (eds.). "Criss-cross methods: A fresh view on pivot algorithms" (PDF). Mathematical Programming, Series B. 79 (1–3). Amsterdam: North-Holland Publishing Co.: 369–395. doi:10.1007/BF02614325. MR 1464775. S2CID 2794181.
- Fukuda, Komei; Namiki, Makoto (March 1994). "On extremal behaviors of Murty's least index method". Mathematical Programming. 64 (1): 365–370. doi:10.1007/BF01582581. MR 1286455. S2CID 21476636.
- Illés, Tibor; Szirmai, Ákos; Terlaky, Tamás (1999). "The finite criss-cross method for hyperbolic programming". European Journal of Operational Research. 114 (1): 198–214. CiteSeerX 10.1.1.36.7090. doi:10.1016/S0377-2217(98)00049-6. ISSN 0377-2217.
- R. Tyrrell Rockafellar (1969). The elementary vectors of a subspace of , in Combinatorial Mathematics and its Applications, R. C. Bose and T. A. Dowling (eds.), Univ. of North Carolina Press, pp. 104–127.
- Roos, C. (1990). "An exponential example for Terlaky's pivoting rule for the criss-cross simplex method". Mathematical Programming. Series A. 46 (1): 79–84. doi:10.1007/BF01585729. MR 1045573. S2CID 33463483.
- Terlaky, T. (1985). "A convergent criss-cross method". Optimization: A Journal of Mathematical Programming and Operations Research. 16 (5): 683–690. doi:10.1080/02331938508843067. ISSN 0233-1934. MR 0798939.
- Terlaky, Tamás (1987). "A finite crisscross method for oriented matroids". Journal of Combinatorial Theory. Series B. 42 (3): 319–327. doi:10.1016/0095-8956(87)90049-9. ISSN 0095-8956. MR 0888684.
- Terlaky, Tamás; Zhang, Shu Zhong (1993). "Pivot rules for linear programming: A Survey on recent theoretical developments". Annals of Operations Research. 46–47 (1): 203–233. CiteSeerX 10.1.1.36.7658. doi:10.1007/BF02096264. ISSN 0254-5330. MR 1260019. S2CID 6058077.
- Todd, Michael J. (1985). "Linear and quadratic programming in oriented matroids". Journal of Combinatorial Theory. Series B. 39 (2): 105–133. doi:10.1016/0095-8956(85)90042-5.
- Wang, Zhe Min (1987). "A finite conformal-elimination free algorithm over oriented matroid programming". Chinese Annals of Mathematics (Shuxue Niankan B Ji). Series B. 8 (1): 120–125. ISSN 0252-9599. MR 0886756.
On the web
- Ziegler, Günter (1998). "Oriented Matroids Today". The Electronic Journal of Combinatorics: DS4: Sep 10–1998. doi:10.37236/25.
- Malkevitch, Joseph. "Oriented Matroids: The Power of Unification". Feature Column. American Mathematical Society. Retrieved 2009-09-14.
External links
- Komei Fukuda (ETH Zentrum, Zurich) with publications including Oriented matroid programming (1982 Ph.D. thesis)
- Tamás Terlaky (Lehigh University) with publications
 , combines a set of objects,
, combines a set of objects,  , with an ordered bipartition
, with an ordered bipartition  of that set into two disjoint subsets:
of that set into two disjoint subsets:  and
and  .
. is called the support of
is called the support of  , is defined as the empty set
, is defined as the empty set  combined with an (ordered) bipartition of it into two empty sets:
combined with an (ordered) bipartition of it into two empty sets:  and
and  .
. is the opposite of
is the opposite of  , if
, if  and
and 
 of the support, we will write
of the support, we will write  for a negative element. In this way, a signed set is just adding negative signs to distinguished elements. This will make sense as a "direction" only when we consider orientations of larger structures. Then the sign of each element will encode its direction relative to this orientation.
for a negative element. In this way, a signed set is just adding negative signs to distinguished elements. This will make sense as a "direction" only when we consider orientations of larger structures. Then the sign of each element will encode its direction relative to this orientation.
 be any set. We refer to
be any set. We refer to  be a collection of signed sets, each of which is supported by a subset of
be a collection of signed sets, each of which is supported by a subset of 





 defined by
defined by  ,
,  , and
, and  . The vectors of an oriented matroid are the compositions of circuits. The vectors
. The vectors of an oriented matroid are the compositions of circuits. The vectors  of an oriented matroid satisfy the following axioms:
of an oriented matroid satisfy the following axioms:


 ,
, 
 and
and  , there is a
, there is a  , such that
, such that
 ,
, , and
, and .
. , a chirotope of rank
, a chirotope of rank  that satisfies the following axioms:
that satisfies the following axioms:
 is not identically zero
is not identically zero and
and  ,
,  , where
, where  is the
is the  such that
such that  for each
for each  , then we also have
, then we also have  .
. is a circuit of the described matroid, then
is a circuit of the described matroid, then  where
where  is a basis. Then
is a basis. Then 
 is the standard set of edges in a minimal cycle. We go along the cycle in the clockwise or anticlockwise direction assigning those edges whose orientation agrees with the direction to the positive elements
is the standard set of edges in a minimal cycle. We go along the cycle in the clockwise or anticlockwise direction assigning those edges whose orientation agrees with the direction to the positive elements  and those edges whose orientation disagrees with the direction to the negative elements
and those edges whose orientation disagrees with the direction to the negative elements  . If
. If  is the set of all such
is the set of all such  , then
, then  and
and  . Then there are only four possible signed circuits corresponding to clockwise and anticlockwise orientations, namely
. Then there are only four possible signed circuits corresponding to clockwise and anticlockwise orientations, namely  ,
,  ,
,  . These four sets form the set of signed circuits of an oriented matroid on the set
. These four sets form the set of signed circuits of an oriented matroid on the set  .
.
 is any finite subset of
is any finite subset of  , then the set of minimal linearly dependent sets forms the circuit set of a matroid on
, then the set of minimal linearly dependent sets forms the circuit set of a matroid on  there is a minimal linear dependence
there is a minimal linear dependence

 . Then the signed circuit
. Then the signed circuit  has positive elements
has positive elements  and negative elements
and negative elements  . The set of all such
. The set of all such  . For any
. For any 
 is a finite set of hyperplanes in
is a finite set of hyperplanes in  , each containing the origin. By picking one side of each hyperplane to be the positive side, we obtain an arrangement of half-spaces. A half-space arrangement breaks down the ambient space into a finite collection of cells, each defined by which side of each hyperplane it lands on. That is, assign each point
, each containing the origin. By picking one side of each hyperplane to be the positive side, we obtain an arrangement of half-spaces. A half-space arrangement breaks down the ambient space into a finite collection of cells, each defined by which side of each hyperplane it lands on. That is, assign each point  to the signed set
to the signed set  with
with  if
if  and
and  if
if  as a cyclic permutation then we define
as a cyclic permutation then we define  to be the sign of the associated permutation. If
to be the sign of the associated permutation. If  is defined as
is defined as

 is the chirotope of the unique orthogonal dual oriented matroid.
is the chirotope of the unique orthogonal dual oriented matroid.
 -dimensional pseudosphere is an embedding of
-dimensional pseudosphere is an embedding of  such that there exists a homeomorphism
such that there exists a homeomorphism  so that
so that  embeds
embeds  as an equator of
as an equator of  . In this sense a pseudosphere is just a
. In this sense a pseudosphere is just a  can be obtained from a pseudosphere arrangement in
can be obtained from a pseudosphere arrangement in  (1967)"
(1967)" , in Combinatorial Mathematics and its Applications, R. C. Bose and T. A. Dowling (eds.), Univ. of North Carolina Press, pp. 104–127.
, in Combinatorial Mathematics and its Applications, R. C. Bose and T. A. Dowling (eds.), Univ. of North Carolina Press, pp. 104–127.