| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Maximum a posteriori estimation" – news · newspapers · books · scholar · JSTOR (September 2011) (Learn how and when to remove this message) |
| Part of a series on |
| Bayesian statistics |
|---|
| Posterior = Likelihood × Prior ÷ Evidence |
| Background |
| Model building |
| Posterior approximation |
| Estimators |
| Evidence approximation |
| Model evaluation |
An estimation procedure that is often claimed to be part of Bayesian statistics is the maximum a posteriori (MAP) estimate of an unknown quantity, that equals the mode of the posterior density with respect to some reference measure, typically the Lebesgue measure. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior density over the quantity one wants to estimate. MAP estimation is therefore a regularization of maximum likelihood estimation, so is not a well-defined statistic of the Bayesian posterior distribution.
Description
Assume that we want to estimate an unobserved population parameter on the basis of observations . Let be the sampling distribution of , so that is the probability of when the underlying population parameter is . Then the function:
is known as the likelihood function and the estimate:
is the maximum likelihood estimate of .
Now assume that a prior distribution over exists. This allows us to treat as a random variable as in Bayesian statistics. We can calculate the posterior density of using Bayes' theorem:
where is density function of , is the domain of .
The method of maximum a posteriori estimation then estimates as the mode of the posterior density of this random variable:
The denominator of the posterior density (the marginal likelihood of the model) is always positive and does not depend on and therefore plays no role in the optimization. Observe that the MAP estimate of coincides with the ML estimate when the prior is uniform (i.e., is a constant function), which occurs whenever the prior distribution is taken as the reference measure, as is typical in function-space applications.
When the loss function is of the form
as goes to 0, the Bayes estimator approaches the MAP estimator, provided that the distribution of is quasi-concave. But generally a MAP estimator is not a Bayes estimator unless is discrete.
Computation
MAP estimates can be computed in several ways:
- Analytically, when the mode(s) of the posterior density can be given in closed form. This is the case when conjugate priors are used.
- Via numerical optimization such as the conjugate gradient method or Newton's method. This usually requires first or second derivatives, which have to be evaluated analytically or numerically.
- Via a modification of an expectation-maximization algorithm. This does not require derivatives of the posterior density.
- Via a Monte Carlo method using simulated annealing
Limitations
While only mild conditions are required for MAP estimation to be a limiting case of Bayes estimation (under the 0–1 loss function), it is not representative of Bayesian methods in general. This is because MAP estimates are point estimates, and depend on the arbitrary choice of reference measure, whereas Bayesian methods are characterized by the use of distributions to summarize data and draw inferences: thus, Bayesian methods tend to report the posterior mean or median instead, together with credible intervals. This is both because these estimators are optimal under squared-error and linear-error loss respectively—which are more representative of typical loss functions—and for a continuous posterior distribution there is no loss function which suggests the MAP is the optimal point estimator. In addition, the posterior density may often not have a simple analytic form: in this case, the distribution can be simulated using Markov chain Monte Carlo techniques, while optimization to find the mode(s) of the density may be difficult or impossible.
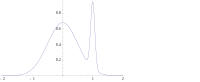
In many types of models, such as mixture models, the posterior may be multi-modal. In such a case, the usual recommendation is that one should choose the highest mode: this is not always feasible (global optimization is a difficult problem), nor in some cases even possible (such as when identifiability issues arise). Furthermore, the highest mode may be uncharacteristic of the majority of the posterior, especially in many dimensions.
Finally, unlike ML estimators, the MAP estimate is not invariant under reparameterization. Switching from one parameterization to another involves introducing a Jacobian that impacts on the location of the maximum. In contrast, Bayesian posterior expectations are invariant under reparameterization.
As an example of the difference between Bayes estimators mentioned above (mean and median estimators) and using a MAP estimate, consider the case where there is a need to classify inputs as either positive or negative (for example, loans as risky or safe). Suppose there are just three possible hypotheses about the correct method of classification , and with posteriors 0.4, 0.3 and 0.3 respectively. Suppose given a new instance, , classifies it as positive, whereas the other two classify it as negative. Using the MAP estimate for the correct classifier , is classified as positive, whereas the Bayes estimators would average over all hypotheses and classify as negative.
Example
Suppose that we are given a sequence of IID random variables and a prior distribution of is given by . We wish to find the MAP estimate of . Note that the normal distribution is its own conjugate prior, so we will be able to find a closed-form solution analytically.
The function to be maximized is then given by
which is equivalent to minimizing the following function of :
Thus, we see that the MAP estimator for μ is given by
which turns out to be a linear interpolation between the prior mean and the sample mean weighted by their respective covariances.
The case of is called a non-informative prior and leads to an improper probability distribution; in this case
References
- ^ Bassett, Robert; Deride, Julio (2018-01-30). "Maximum a posteriori estimators as a limit of Bayes estimators". Mathematical Programming: 1–16. arXiv:1611.05917. doi:10.1007/s10107-018-1241-0. ISSN 0025-5610.
- Murphy, Kevin P. (2012). Machine learning : a probabilistic perspective. Cambridge, Massachusetts: MIT Press. pp. 151–152. ISBN 978-0-262-01802-9.
- ^ Young, G. A.; Smith, R. L. (2005). Essentials of Statistical Inference. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge: Cambridge University Press. ISBN 978-0-521-83971-6.
- DeGroot, M. (1970). Optimal Statistical Decisions. McGraw-Hill. ISBN 0-07-016242-5.
- Sorenson, Harold W. (1980). Parameter Estimation: Principles and Problems. Marcel Dekker. ISBN 0-8247-6987-2.
- Hald, Anders (2007). "Gauss's Derivation of the Normal Distribution and the Method of Least Squares, 1809". A History of Parametric Statistical Inference from Bernoulli to Fisher, 1713–1935. New York: Springer. pp. 55–61. ISBN 978-0-387-46409-1.
 on the basis of observations
on the basis of observations  . Let
. Let  be the
be the  is the probability of
is the probability of 

 over
over 
 is the domain of
is the domain of 

 goes to 0, the
goes to 0, the  ,
,  and
and  with posteriors 0.4, 0.3 and 0.3 respectively. Suppose given a new instance,
with posteriors 0.4, 0.3 and 0.3 respectively. Suppose given a new instance,  of
of 
 is given by
is given by  . We wish to find the MAP estimate of
. We wish to find the MAP estimate of 


 is called a non-informative prior and leads to an improper
is called a non-informative prior and leads to an improper 