
Relations are ways in which several entities stand to each other. They usually connect distinct entities but some associate an entity with itself. The adicity of a relation is the number of entities it connects. The direction of a relation is the order in which the elements are related to each other. The converse of a relation carries the same information and has the opposite direction, like the contrast between "two is less than five" and "five is greater than two". Both relations and properties express features in reality with a key difference being that relations apply to several entities while properties belong to a single entity.
Many types of relations are discussed in the academic literature. Internal relations, like resemblance, depend only on the monadic properties of the relata. They contrast with external relations, like spatial relations, which express characteristics that go beyond what their relata are like. Formal relations, like identity, involve abstract and topic-neutral ideas while material relations, like loving, have concrete and substantial contents. Logical relations are relations between propositions while causal relations connect concrete events. Symmetric, transitive, and reflexive relations are distinguished by their structural features.
Metaphysical difficulties like the question of where relations are located lie at the center of discussions of their ontological status. Eliminativism is the thesis that relations are mental abstractions that are not a part of external reality. A less radical position is reductionism, which claims that relations can be explained in terms of other entities, like monadic properties, and are not a substantial addition to reality. According to realists, relations have a mind-independent existence. A strong form of realism is relationalism, which states that all of reality is relational at its most basic level. Historically, eliminativism and reductionism were the dominant views. This only changed toward the end of the 19th century, when various developments in the fields of mathematics, logic, and science prompted a more realist outlook.
Definition and essential features
A relation is a manner in which multiple entities stand to each other. It is a connection or association between entities and can be understood as a feature characterizing these entities as a whole. Many relations hold between distinct entities. For example, the first-born sibling stands in the relation of being older than to their other siblings. But an entity can also stand in a relation to itself. For instance, every entity stands in the relation of identity to itself. Relations can hold between diverse entities, including objects, people, and concepts. If a relation holds between entities then the relation together with the entities constitutes a fact or state of affairs.
The word "relationship" is often used as a synonym. The entities related to each other are called the relata. The term "relation" comes from the Latin terms relatio and referre, which mean reference or towardness.
In mathematics and logic, relations are defined as set-theoretic structures. For example, the relation less than is defined as the set of all ordered pairs in which the first element is less than the second element. This set includes pairs like , , and . Mathematical functions are a special type of relation in which one or several elements are uniquely associated with exactly one other element.
Relations have various characteristic features, like the number of relata they have and the direction in which they connect them. They are closely associated with properties and share several aspects with them.
Adicity
The adicity of a relation is the number of places or relata it has. The terms "arity" and "degree" are used as synonyms. For instance, the relation being larger than has an adicity of two since it involves two entities: a smaller entity and a larger entity. Another example is the relation of being adjacent to. Relations with an adicity of two are called dyadic or binary. Triadic or ternary relations have an adicity of three, like the relation of giving, which involves a giver, a receiver, and a given object. The relation of being between is also triadic since it requires two entities on the sides and one in the middle, as in "5 is between 2 and 23".
Unigrade relations are relations that have a fixed adicity: they always apply to the same number of entities. They contrast with multigrade relations, for which the number of their relata varies from one occasion to another. It is controversial whether there are genuine multigrade relations. Some theorists, like David M. Armstrong, argue that the adicity of a relation is an essential feature of it. According to this view, there are no multigrade relations on the fundamental level of reality. However, this view is not generally accepted and some cases of multigrade relations have been suggested. Putative examples include causal relations (which may relate several causes to several effects), logical consequence (which relates several premises to a conclusion they support), and expressions like being the tallest among (for which the adicity depends on the size of the comparison group). Multigrade predicates are also common in everyday language. For instance, the predicate "lift" is dyadic in the sentence "John is lifting a table" and triadic in the sentence "John and Mary are lifting a table". Other examples are predicates that have optional arguments, as in the sentences "John is eating a cake" and "John is eating".
Direction and converse
The direction of a relation is the order in which the elements are related to each other. For instance, if Abelard loves Eloise then the relation of loving goes from Abelard to Eloise. If Eloise loves Abelard then the direction goes in the opposite direction. Both of these facts have the same constituents. They are only distinguished by their direction. Only non-symmetric relations have a direction since the order of the relata does not make a difference for symmetric relations.
The converse of a non-symmetric relation is a second relation that always accompanies the first relation but has a different order of elements. For example, the converse of above is below. This means that whenever x is above y then y is below x. The same is the case for relations like coming before and coming after as well as being a parent of and being a child of. Binary relations have exactly one converse while tertiary and higher-degree relations have several converses.
A relation and its converse carry the same information. For this reason, it is controversial whether they should be considered as two distinct relations instead of seeing them as the same relation. This difficulty has prompted some philosophers to conceptualize the directional aspect of non-symmetric relations differently or to deny the existence of converse relations. According to positionalism, relations do not have a direction but have different unique positions that are filled by their relata. For instance, the relation love has two positions: one for the lover and one for the beloved. This view explains how relata can play different roles in a relation without implying that the relation has a direction or a converse.
Contrast to properties
Relations are usually contrasted with properties. Properties are held by a single entity and express what this entity is like. Relations connect several entities and are features that apply to them as a whole. A closely associated contrast is that properties belong to entities or inhere in them while relations are not found in the relata but stand between them.
However, there are also many parallels between properties and relations and there is no general agreement on a strict dichotomy between the two. Both are often used to describe and explain repeating patterns in the world and many of the ontological distinctions applied to properties also affect relations. For example, both properties and relations may be understood as universals that are instantiated by individuals at a specific place and time. Like properties, relations are either determinable or determinate. Determinable relations are not specified, like the relation of being distant from. Determinate relations are fully specified, like the relation of being exactly one meter distant from.
It is possible to conceptualize properties and propositions as special types of relations. According to this view, the difference between these phenomena only concerns how many entities they apply to: regular relations are polyadic and thus apply to several entities; properties are monadic relations and only apply to a single entity; propositions are relations with a degree of zero and do not apply to any entities.
The opposite perspective is also possible: to conceptualize relations as polyadic or relational properties. It is usually accepted that relational properties accompany relations: if x stands in a relation to y, then x has the relational property of bearing a relation to y. For example, since Antony was married to Cleopatra, he had the relational property of being married to Cleopatra. However, it is not generally accepted that relations are correctly understood as or can be reduced to relational properties. Historically, properties have received significantly more attention from metaphysicists than relations.
Types
Various types of relations are distinguished in the academic literature based on their ontological status, the domains they apply to, and the structures they form.
Internal and external
An influential distinction differentiates between internal and external relations. A relation is internal if it only depends on what the relata are like: it is determined by the characteristics or the nature of the relata alone. External relations are not fixed this way and carry characteristics that go beyond the intrinsic features of their relata. Mathematical relations between numbers are examples of internal relations. For instance, the number six stands in the relation of being greater than to the number five. This relation is internal because it is essential to the numbers six and five that six is greater than five. Other traditional examples of internal relations are resemblance and difference. Spatial relations are normally understood as external relations, like the relation of a book to the table it is lying on. The same is true for temporal and causal relations.

However, the precise characterization of the distinction between internal and external relations is disputed and there are various incompatible ways to define them. According to G. E. Moore, a relation is internal if it follows from the existence of its relata that the relation also exists. This means that the relation is essential to the relata and the relata cannot exist without this relation. For Moore, external relations are different since they could fail to obtain even if its relata exist. Another definition is defended by philosophers like Armstrong, who hold that a relation is internal if it is necessitated by the properties or the intrinsic features of the relata. David K. Lewis provides a slightly different formulation by claiming that internal relations supervene on the intrinsic properties of their elements. Some philosophers talk of ideal relations to refer to relations that solely depend on the qualities of the related terms, in contrast to real relations, for which this is not the case.
The difference between these definitions affects whether some relations are characterized as internal or external. An example is the relation of having the same shape. This relation applies if x is a cube and y is also a cube. According to Armstrong, this relation is internal since it only depends on the intrinsic nature of x and y. This is not the case for Moore since y could have been a sphere rather than a cube, meaning that the relation is external since it is not necessitated by the existence of x and y.
The difference between internal and external relations has various consequences for the ontological status of relations. According to a common view, internal relations do not form part of reality on the most fundamental level since they supervene on their relata. In this regard, they are already included in some sense in the relata and constitute no addition to being. That is not the case for external relations, which are more than the entities they connect and thus introduce additional ontological commitments. Discussions about the existence of relations usually focus on the question of whether external relations exist. One difficulty in this regard is where to locate them since it seems that they are not contained within the relata while they also cannot exist without them.
Formal and material
Another distinction is between formal and material relations, sometimes also termed thin and thick relations. Formal relations involve abstract ideas that do not carry any concrete content. According to a commonly held view, all formal relations are internal. They are often characterized as topic-neutral, meaning that they pertain to all categories of being. Material relations are associated with concrete ideas. They involve specific and substantial contents that are accessible to perceptual experience. Examples of formal relations are identity, entailment, being greater than, set membership, and resemblance. By contrast, the relations of collision, smiling, loving, killing, and giving are material relations.
Logical and causal
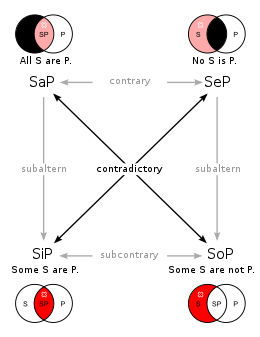
Logical relations are relations between elements of thought, specifically between propositions or statements. Two propositions are logically related if the truth value of one depends on the truth value of the other. In this regard, it is not important whether the propositions are true but only how the truth value of one proposition would affect the truth value of the other. For instance, the claims "John has a high IQ and is immensely popular" and "John has a high IQ" are logically related since the first claim cannot be true if the second claim is false. Logical relations are discovered through a priori reasoning rather than perceptual experience and are studied by logic. They are often used to demonstrate or prove a claim.
Of primary interest in logic is the relation of logical consequence or entailment. This relation holds between the premises of an argument and its conclusion if the argument is governed by a valid rule of inference. It determines what follows logically from what and is present if the truth of the premises ensures the truth of the conclusion. This means that if the premises are true, the conclusion cannot be false. Other examples of logical relations are being contrary and being contradictory. Two statements are contradictory if it is necessary that one is true and the other is false, like the statements "the coffee is cold" and "the coffee is not cold". Two statements are contraries if both can be false but both cannot be true, like the statements "the coffee is cold" and "the coffee is hot".
Causal relations are cause-effect relations between concrete events. This is the case if an earlier event brings about a later event. An example is a white billiard ball that hits a red billiard ball, which in turn starts rolling toward a corner pocket. In this case, there is a causal relation between the collision-event and the rolling-event. Causal relations are studied by the empirical sciences and can be known through perceptual experience. They play a role in explaining why something happened.
Causal relations are traditionally understood as external relations. According to this view, they obey external causal laws or laws of nature that determine how effects follow from causes and are not fixed by the internal nature of the involved events. They are traditionally seen as contingent: they are the way they are but they could have been different because the causal laws could have been different. An alternative position understands causation not in terms of causal laws but in terms of the powers of objects. In this case, the effect is a manifestation of the powers of the involved objects. According to this view, causal relations are internal relations if powers are understood as intrinsic properties of objects.
One difficulty in distinguishing between causal and logical relations is that both can be expressed with the term "because". For instance, the sentence "John came back because he loved her" expresses a causal relation with love being the cause of John's return. The sentence "John loved her, because he came back" expresses a logical relation in which the existence of John's love is inferred from the fact that he came back.
Spatial and temporal
Spatial and temporal relations structure the physical world and organize how concrete objects and events stand to each other. Spatial relations affect where entities are located and how close or distant they are from each other. Examples are being three feet from, being below, and being within. Temporal relations concern when something happens relative to something else. Examples are occurring before, occurring after, and occurring simultaneously. It is usually held that spatiotemporal relations only hold between concrete objects but not between abstract objects. Spatial and temporal relations are normally categorized as external relations.
The ontological status of spatial and temporal relations depends on how space and time are conceived. The theory of relationalism states that spacetime is nothing but the spatial and temporal relations in which entities stand to each other. According to this view, spatial and temporal relations are fundamental and constitute spacetime. A different view is substantivalism, which holds that spacetime is a substance that exists independently of the entities that occupy it. Both relationalists and substantivalists accept regular statements about spatiotemporal relations, for example, that "the two towers of the Golden Gate Bridge are 4,200 feet apart". According to relationalists, this sentence is true because there is a fundamental spatial relation between the towers themselves. According to substantivalists, this is true because the two towers occupy two distinct and spatially distant regions in the spacetime substance.
In classical physics, space and time are understood as independent dimensions that are absolute and can be measured and analyzed separately from each other. In modern physics, space and time are seen as interdependent dimensions that form a unified continuum whose curvature is affected by the presence of mass and energy.
By structural features
Binary relations are often distinguished based on several formal or structural features of how their elements are connected to one another. Symmetric relations always come in pairs: if x is related to y then y is related to x. An example is the relation being as old as: if Tom is as old as Zoe then Zoe is as old as Tom. Symmetric relations contrast with non-symmetric relations, for which this pair-like behavior is not always observed. An example is the love-relation: if Dave loves Sara then it is possible but not necessary that Sara loves Dave. A special case of non-symmetric relations is asymmetric relations, which only go one way. An example is the relation being heavier than: if Ben is heavier than Nia then it is not possible at the same time that Nia is heavier than Ben. Symmetric relations are not sensitive to how their elements are ordered since they go both ways. However, the order of the elements matters for non-symmetric relations.
A further distinction is between transitive and intransitive relations. Transitive relations exhibit a chain-like nature: if x is related to y and y is related to z, then x is related to z. An example is the relation being larger than: if a truck is larger than a car and a car is larger than a bicycle then a truck is larger than a bicycle. A relation is intransitive if this chain-like behavior is not always present. An example is the relation being a parent: if Tess is a parent of Bob and Bob is a parent of Carol, then it is not automatically the case that Tess is a parent of Carol.
Another distinction is between reflexive and irreflexive relations. Reflexive relations are those in which each entity is related to itself. An example is the relation being as old as since every entity is as old as itself. Irreflexive relations are relations that never connect an entity to itself. An example is the relation being a sibling of: no one is their own sibling.
These structural features are used to define further types of relations, like equivalence and strict partial order. An equivalence relation is a relation that is reflexive, symmetric, and transitive, like equality expressed through the symbol "=". A strict partial order is a relation that is irreflexive, anti-symmetric, and transitive, like the relation being less than expressed through the symbol "<".
Ontological status
Various debates in metaphysics are concerned with the ontological status of relations. Relations come with certain problems that are not present for other ontological categories, like substances and monadic properties. They are different from substances because they depend on the entities they connect. They are different from properties since they apply to several entities and cannot be located in any one of their relata.
The ontological status of relations is disputed and various theories have been proposed. They are often divided into realism and anti-realism. Realists hold that relations have mind-independent existence in external reality, which is denied by anti-realists. However, various intermediate positions between these views can be distinguished. Strict anti-realists or eliminativists deny that there are any relations. A slightly weaker position sees relations as mental inventions or projections. Another perspective is to accept that relations exist while regarding them as non-fundamental entities. This type of position is taken by reductionists, who claim that relations are emergent entities that can be reduced to other entities. Strong realists advance a more robust view and see relations as part of the fundamental ontological inventory of reality. The difference between internal and external relations is central to their ontological status and the two types are often treated separately.
The issue of the ontological status of relations is closely connected to the problem of the one and the many. This problem consists in explaining how reality can at the same time be both a multiplicity (because there are many distinct entities) and a unity (because all the distinct entities participate in one common reality).
Location problem
Many of the difficulties associated with the ontological status of relations are connected to the location problem. The location problem consists of the question of where relations are located. For example, the sentence "Glasgow is west of Edinburgh" describes the location of two cities based on the relation being west of. However, it does not specify where the relation itself is located.
Different solutions to the location problem have been suggested. One suggestion is that the location of relations is divided. According to this view, the relation of being west of resides in both Glasgow and Edinburgh together. A different approach is to hold that relations exist in a place between their relata. A further theory states that relations are abstract objects that do not have a location in space and time.
A closely connected issue concerns how relations depend on their relata. Like properties, relations are traditionally conceived as accidents or dependent entities. A traditionally common view says that properties are located in the object they characterize. However, this solution is more difficult for relations, specifically for external relations, since they do not inhere in a single entity but form connections between entities. Their external location makes it more difficult to conceive how they can be dependent entities at the same time. The difficulties concerning the location of relations have prompted some philosophers to deny that relations exist or to hold that they exist only as ideas in the mind.
Eliminativism
Eliminativists about relations hold that relations do not exist. They often see relations as intellectual abstractions that are not part of reality at the most fundamental level. Some eliminativists defend this view for all relations while others focus specifically on external relations. They often justify their position by the ontological problems associated with relations, such as the location problem. Metaphysical monists, like some defenders of absolute idealism, often reject the existence of genuine relations by claiming that there exists only one ultimate subject of predication.

A well-known argument for eliminativism is called Bradley's regress. It was formulated by F. H. Bradley, who argues that relations do not exist because they involve a vicious infinite regress. Bradley understands relations as universals and holds that a relation can only connect two entities if it is related to them. He claims that to be related to them, a second relation is required to relate the first relation to its relata. However, the same problem is repeated on the level of the second relation, which requires a third relation, and so on. This leads to a vicious infinite regress since the same problem arises for all additional relations. Bradley concludes from the resulting paradox that relations do not exist.
The conclusion of Bradley's regress is not generally accepted and various arguments have been formulated to reject it. One approach is to distinguish between relations as universals and relational facts corresponding to particular instances. According to this view, the connection between a relation and its relata is made by the fact that instantiates the relation without the need for a second relation. A closely connected explanation understands relations not as universals but as particular entities, so-called tropes. Opponents of these approaches have argued that they fail to truly solve the problem since they do not explain how facts or tropes connect a relation to its relata without requiring a second relation. Another argument against Bradley's regress rejects the initial assumption that relations need to be related to the relata.
Objections to eliminativism are often based on the idea that relations are required to describe reality. For instance, relations seem to be an indispensable part of mathematics and the empirical sciences.
Reductionism
Reductionism is the view that relations can ultimately be reduced to or explained in terms of non-relational entities. In this regard, they are not a substantial addition to reality but only accompany other phenomena. Some theorists understand reductionism as a form of anti-realism while others hold that reductionism allows that relations exist in a weak sense but denies that they are part of the most fundamental level of reality.
A common form of reductionism states that relations can be understood in terms of the monadic properties of the related entities. For example, the mountain Ben Vorlich stands in the relation of being taller than to its neighbor Ben Vane. This is explained by the properties of the two mountains: Ben Vorlich is 3094 feet high while Ben Vane is 3002 feet high. According to this view, no additional relational facts besides these properties are required. Another example is the relation of similarity, which is often analyzed in terms of shared properties.
The claim that all relations, including external relations, can be reduced to monadic properties is controversial. For instance, it is not clear how spatial relations can be analyzed this way. A further argument against reductionism comes from modern physics and holds that the non-relational properties it discusses are not sufficient to explain all phenomena.
Reductionism is common when applied to internal relations, but it is not universally accepted. One anti-reductionist argument holds that some kind of minimal formal relation between the monadic properties themselves is required even in the case of internal relations. For example, to explain that Ben Vorlich is higher than Ben Vane, the properties being 3094 feet high and being 3002 feet high by themselves are not sufficient if one does not assume that the relation of being greater than holds between these properties.
Realism
Realists hold that relations are part of reality. This view is usually combined with the claim that relations have mind-independent existence. In a strong form, it states that relations belong to the most fundamental level of reality. However, there are also weaker forms of realism. They hold that relations are real but do not exist on the most fundamental level. According to this view, they emerge from non-relational features and are in this sense "no addition to being".
Some realists understand relations as universals. According to this view, relations are repeatable and can be instantiated by different groups of individuals. A different view holds that relations are tropes or non-repeatable particulars.
Relationalism
Relationalism is a strong form of realism about relations. In its widest sense, it states that all of reality is relational at its most fundamental level and denies the existence of non-relational properties. The terms "relationism" and "relational ontology" are sometimes used as synonyms. Relationalism contrasts with substantivalism, also known as substantivism, which sees substances, and not relations, as the fundamental constituents of reality.
One core intuition motivating relationalism is that a key to understanding any object is to grasp how it is related to other objects. Some relationalists state that objects do not exist at all while others hold that they only exist as dependent entities. For example, the position of ontic structuralism claims that objects are structures made up of relations. According to philosopher Randal Dipert, the world is made up of relations that form the structure of a mathematical graph and the concrete entities in it are subgraphs.
Relationalism is a controversial view when understood in its strongest form as a theory of reality in general. Besides its clash with common sense, one difficulty is that relations are usually understood as dependent entities that apply to the objects they connect rather than as independent entities that could exist without their relata. Another difficulty is that purely relational structures seem to be abstract objects that cannot by themselves account for the concrete reality they aim to describe.
Some relationalists defend more restricted theories by limiting their claims to specific domains rather than trying to explain reality as a whole. In the philosophy of space and time, relationalism is the view that spacetime is not a substance, as substantivalists claim, but a network of spatiotemporal relations between individual physical phenomena. In the philosophy of perception, relationalism about color is the view that colors are not regular monadic properties of objects but relations between perceptual circumstances and the subjects that perceive them. In the philosophy of sociology, relationalism is an approach that investigates wide social phenomena by studying the relations between interactants. Examples are seeing society as the totality of interactions between people or understanding the world of art in terms of the relations between artists, producers, audiences, and critics.
History

The history of the philosophy of relations can roughly be divided into two periods. Traditionally up until the late 19th century, metaphysicists were suspicious about the nature of relations. They usually regarded them as lower entities that do not play a role on the fundamental level of reality. This outlook changed in the 19th century, when various developments in the fields of mathematics, logic, and science prompted philosophers to reconceptualize the nature of relations and the need for relations to describe reality on its most basic level.
Aristotle's distinction between substances and accidents was influential in how relations were conceived by later philosophers. Substances are the fundamental constituents of reality. They exist in themselves and are not predicable of something else, like an individual man or a horse. Accidents cannot exist without a substance. They are possible but non-necessary modifications of substances, like being in a sitting position. Aristotle conceived relations as the lowest form of accidents that depend not just on substances but also on other accidents. Many subsequent philosophers accepted the idea that relations are non-substantial entities that are unable to exist on their own and depend on other entities. For example, the neo-Platonists Plotinus and Porphyry followed Aristotle in seeing relations as accidents while emphasizing at the same time that relations are real entities.
The nature and role of relations were discussed in detail in medieval philosophy, specifically by scholastic philosophers. They agreed with Aristotle that relations are accidents. A common approach was to reduce relations to pairs of monadic properties. This approach was exemplified by Peter Abelard and William Ockham, who explained relations in terms of non-relational qualities possessed by the relata. For instance, they held that if Socrates is similar to Theaetetus then this is because they share certain qualities, like color. Some scholastic philosophers, like Peter Auriol, rejected relations and held instead that they are merely mental associations of entities not found outside the mind. A different approach was followed by Albert the Great and John Duns Scotus, who understood relations as a distinct and irreducible type of entity. Thomas Aquinas defended a middle position by holding that some relations have a substantial foundation in reality, like being a father, while others merely exist on the verbal level, like being moved by.
According to a common view in the modern period, relations are reducible to other entities or exist merely in the mind. For example, Thomas Hobbes defended a form of nominalism according to which only individuals have full existence. This implies that relations lack a proper ontological status and only exist in the mind as a form of mental comparison.

Gottfried Wilhelm Leibniz rejected the fundamental reality of relations based on the claim that they would lack a proper location in this case. These ontological difficulties prompted Leibniz to propose his monadology, according to which reality is made up of windowless and unconnected monads. For him, relations are emergent entities that arise from the intrinsic properties of the relata. They are understood as pairs of monadic properties and not as ontologically distinct entities. For instance, if Adam is the father of Cain then Adam has the property of being a father of Cain and Cain has the property of being a child of Adam. In this regard, relations have a foundation in reality but are at the same time mental constructions that arise by comparing things.
Leibniz's idealist outlook on relations influenced Immanuel Kant, who included relation in his system of categories as one of the four basic groups of categories. It covers the topic of how human minds organize and understand objects and concepts in terms of their mutual connections, dependencies, and interactions, for example, how properties inhere in substances and how effects depend on their causes. Kant gave a prominent role to relations and held that phenomenal reality is at its core constituted by relations. This idealist outlook on the importance of relations was also defended by Georg Wilhelm Friedrich Hegel, who argued that the nature, meaning, and value of things arises from how they participate in relations.

 Charles Sanders Peirce compared relations to molecules formed by bonds between elements.
Charles Sanders Peirce compared relations to molecules formed by bonds between elements.
Difficulties about the ontological status of relations were also reflected in how they were treated in the field of logic before modern formal logic. For example, Aristotelian logic restricts itself to propositions in a subject-predicate form in which the predicate expresses qualities or attributes of a single entity in the subject position. Modern logic, by contrast, also allows reasoning with relations to express how several entities stand to each other. An important early development in this regard was the formulation of the logic of relations by Augustus De Morgan in the 19th century. It introduces formal devices to assess the validity of reasoning regarding relations, including compound relations like combining the relations of father of and brother of into uncle of. De Morgan's logic of relations was further developed by Charles Sanders Peirce, who conceptualized the adicity of relations in analogy to chemical elements that form molecules based on their valency.
The problem of relations played a central role in Bradley's philosophy. He defended a form of monist idealism. According to it, there are no real separate entities and only one substance exists in the form of an idea or experience. For Bradley, the plurality of things in the world, as it appears to us, is ultimately an illusion. A consequence of this view is that there are no genuine relations since there are no distinct entities that could be related to each other. He argued for this conclusion by trying to show that relations cannot exist because they would involve a vicious infinite regress.

Various early analytic philosophers, like Moore and Bertrand Russell, rejected Bradley's monist idealism and the associated theory of relations. Moore based his rejection of Bradley's doctrine on the claim that it is not in tune with common sense, which favors a pluralistic ontology with genuine relations. Moore was further influential in developing the distinction between internal and external relations. Russell argued in favor of the reality of external relations by pointing out that they are required to give an accurate scientific description of the external world. Arguments for the reality of relations based on science were also defended by David Malet Armstrong. He conceived relations as universals that are instantiated in spacetime. According to him, it is the role of science to determine which relational universals exist.
Various other solutions to the problem of relations have been suggested. For example, Gottlob Frege understood them as incomplete objects with open positions. They are completed when these positions are filled by the relata. In this regard, relations do not occur on their own and exist only insofar as they establish connections between other entities. A further approach is found in Ludwig Wittgenstein's early philosophy, where he stated that objects can form connections with each other without requiring any additional elements. In this way, they are similar to chains: the different links of the chain are directly connected to each other without the additional need for relational entities to establish the connection.
References
Citations
-
- Bogen 2005, p. 798
- MacBride 2020, lead section
- Borchert 2006, pp. 24–25, Ontology
-
- Bogen 2005, p. 798
- MacBride 2020, lead section
- Thompson 2000, Relation
- ^ Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
- MW staff 2023
-
- MW staff
- Orilia & Paolini Paoletti 2022, §1.5 Relations
-
- Mattingly 2003, p. 40, relation
- Hoad 1993, p. 396
-
- Sider 2010, p. 14
- DeLancey 2017, p. 200
- Bogen 2005, p. 798
- Heil 2009, p. 310
-
- Even & Medina 2012, p. 9
- DeLancey 2017, p. 203
-
- Le Poidevin et al. 2009, p. 579
- MacBride 2020, §1. Preliminary Distinctions, §4. The Nature of Relations: Order and Direction
- Bacon, Detlefsen & McCarty 2013, p. 7
- ^
- MacBride 2020, lead section
- Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
-
- Le Poidevin et al. 2009, p. 579
- MacBride 2020, §1. Preliminary Distinctions
- Bacon, Detlefsen & McCarty 2013, p. 7
- Kim, Sosa & Rosenkrantz 2009, p. 545
-
- Le Poidevin et al. 2009, p. 579
- MacBride 2020, §1. Preliminary Distinctions
- Bacon, Detlefsen & McCarty 2013, p. 7
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Sider 2010, p. 14
-
- MacBride 2020, §1. Preliminary Distinctions
- Armstrong 2010, pp. 23–24, 3. Relations
- Ehring 2011, p. 21
- ^ MacBride 2020, §1. Preliminary Distinctions
-
- Armstrong 2010, pp. 23–24, 3. Relations
- MacBride 2018, p. 232
-
- MacBride 2020, §1. Preliminary Distinctions
- Armstrong 2010, pp. 23–24, 3. Relations
-
- MacBride 2020, §4. The Nature of Relations: Order and Direction
- Kim, Sosa & Rosenkrantz 2009, p. 545
- MacBride 2007, p. 25
- Orilia & Paolini Paoletti 2022, §1.5 Relations
- Orilia & Paolini Paoletti 2022, §1.5 Relations
-
- MacBride 2020, §4. The Nature of Relations: Order and Direction
- Kim, Sosa & Rosenkrantz 2009, p. 545
- MacBride 2007, p. 25
-
- MacBride 2020, §1. Preliminary Distinctions
- Parry & Hacker 1991, p. 251
- MacBride 2020, §4. The Nature of Relations: Order and Direction
-
- MacBride 2020, §4. The Nature of Relations: Order and Direction
- MacBride 2007, pp. 26–27
-
- MacBride 2020, §4. The Nature of Relations: Order and Direction
- Koons & Pickavance 2017, pp. 213–214
- Orilia & Paolini Paoletti 2022, §1.5 Relations
- Koons & Pickavance 2017, pp. 213–214
-
- MacBride 2020, §4. The Nature of Relations: Order and Direction
- Orilia & Paolini Paoletti 2022, §1.5 Relations
-
- Heil 2009, p. 310
- Armstrong 2010, p. 23, 3. Relations
- Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
- Sider 2010, p. 13
-
- Heil 2009, p. 310
- Armstrong 2010, p. 23, 3. Relations
- Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
- Borchert 2006, pp. 24–25, Ontology
-
- Armstrong 2010, p. 23, 3. Relations
- Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
- Armstrong 2010, p. 23, 3. Relations
-
- Orilia & Paolini Paoletti 2022, lead section, §1.5 Relations
- Armstrong 2010, p. 23, 3. Relations
- MacBride 2020, §1. Preliminary Distinctions
- Heil 2009, p. 310
- Heil 2009, pp. 310, 313–314
- ^ Heil 2009, p. 310
-
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Bogen 2005, pp. 798–799
- MacBride 2020, §1. Preliminary Distinctions
-
- MacBride 2020, §1. Preliminary Distinctions
- Heil 2009, p. 316
- Armstrong 2010, pp. 24–25, 3. Relations
- Heil 2009, p. 313
- ^ Armstrong 2010, p. 25, 3. Relations
-
- Rickabaugh & Moreland 2023, p. 47
- Hazlett 2016, p. 220
- Bogen 2005, pp. 798–799
-
- MacBride 2020, §1. Preliminary Distinctions
- Heil 2009, p. 313
- Bogen 2005, pp. 798–799
- Maurin 2013, pp. 144–145
- Monnoyer 2013, pp. 110–111
-
- MacBride 2020, §1. Preliminary Distinctions
- Maurin 2013, pp. 144–145
- Monnoyer 2013, pp. 110–111
-
- MacBride 2020, §1. Preliminary Distinctions
- Lewis 1999, p. 129
- ^ Bogen 2005, p. 799
-
- Maurin 2013, pp. 144–145
- MacBride 2020, §1. Preliminary Distinctions
- Monnoyer 2013, pp. 110–111
-
- Bogen 2005, pp. 798–799
- Armstrong 2010, p. 25, 3. Relations
-
- Armstrong 2010, p. 25, 3. Relations
- Heil 2009, p. 314
- Orilia & Paolini Paoletti 2022, §1.5 Relations
-
- Heil 2009, pp. 313–314
- Orilia & Paolini Paoletti 2022, §1.5 Relations
- Bogen 2005, pp. 798–799
- Heil 2009, p. 315
-
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Trautwein 2011, p. 126
- ^ MacBride 2020, §3. Reductionism about Internal Relations
-
- MacBride 2020, §3. Reductionism about Internal Relations
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Trautwein 2011, p. 126
- Clementz 2014, p. 218
- Clementz 2014, p. 218
-
- MacBride 2020, §3. Reductionism about Internal Relations
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Trautwein 2011, p. 126
- Clementz 2014, pp. 217–218
- ^ EB staff 1998
- ^
- ^ Turetzky 2019, pp. 64–67
- ^ Piaget 2002, p. 10
-
- McKeon, lead section
- Papineau 2012, p. 146
- Heil 2009, p. 317
-
- Heil 2009, p. 317
- Mumford 2004, p. 94
-
- Heil 2009, p. 317
- Marmodoro & Yates 2016, p. 139
-
- Patard & Brisard 2011, p. 126
- Piaget 2002, p. 10
-
- Dasgupta 2015, p. 601
- Hazlett 2016, p. 220
- Hazlett 2016, p. 220
-
- Rickles 2008, p. 24
- Dasgupta 2015, pp. 601–602
- Heil 2009, p. 318
- Dasgupta 2015, pp. 601–602
-
- Bogen 2005, p. 798
- MacBride 2020, §1. Preliminary Distinctions
- DeLancey 2017, pp. 201–202
- Sider 2010, p. 114
- ^
- Bogen 2005, p. 798
- DeLancey 2017, pp. 201–202
- Sider 2010, p. 114
-
- Makridis 2022, p. 456
- Bogen 2005, p. 798
-
- Wallis 2003, p. 98
- Berztiss 2014, p. 73
- Wallis 2003, p. 100
- ^
- Bogen 2005, p. 799
- Heil 2009, p. 310
- ^ MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
-
- Heil 2009, pp. 312, 319–320
- Marmodoro & Yates 2016, p. 52
- Borchert 2006, pp. 24–25, Ontology
- Galluzzo & Loux 2015, p. 130
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
-
- Heil 2009, pp. 312, 319–320
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress, §3. Reductionism about Internal Relations
-
- Clarke 2015, pp. 109–110
- Joad 1929, pp. 87–88
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Marmodoro & Yates 2016, p. 74
-
- Heil 2009, pp. 315–316
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Bogen 2005, p. 799
- Heil 2009, p. 310
- Marmodoro & Yates 2016, p. 74
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Bogen 2005, p. 799
- Heil 2009, p. 310
-
- Marmodoro & Yates 2016, p. 76
- Heil 2009, p. 312
- Hood 2004, pp. 1–3, 6–7
- Kim, Sosa & Rosenkrantz 2009, p. 545
-
- Heil 2009, pp. 310, 315–316
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Bogen 2005, p. 799
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Heil 2009, pp. 315–316
-
- Marmodoro & Yates 2016, p. 74
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Heil 2009, pp. 315–316
-
- Bogen 2005, p. 798
- Heil 2009, pp. 310, 315
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Cowling 2017, pp. 124–125
- Heil 2009, pp. 315–316
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Szatkowski 2022, p. 120
-
- Heil 2009, p. 312
- MacBride 2020, §3. Reductionism about Internal Relations
-
- MacBride 2020, §3. Reductionism about Internal Relations
- Heil 2009, pp. 312, 315–316
- Marmodoro & Yates 2016, pp. 41, 47
-
- Marmodoro & Yates 2016, pp. 60–61
- Heil 2009, p. 310
- Orilia & Paolini Paoletti 2022, §1.5 Relations
- Marmodoro & Yates 2016, p. 61
-
- Marmodoro & Yates 2016, p. 61
- Orilia & Paolini Paoletti 2022, §1.5 Relations
-
- Marmodoro & Yates 2016, p. 61
- Orilia & Paolini Paoletti 2022, §1.5 Relations
- MacBride 2020, §3. Reductionism about Internal Relations
-
- Heil 2009, p. 319
- Marmodoro & Yates 2016, pp. 36–37
- Heil 2009, p. 319
-
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Armstrong 2010, pp. 23–25
- Kim, Sosa & Rosenkrantz 2009, p. 545
-
- Heil 2009, p. 310
- Runggaldier 2009, p. 248
- Lupisella 2020, p. 70
-
- Dainton 2006, p. 73
- Heil 2021, 10.2 Not Nothings but Not Somethings Either
- Heil 2009, p. 311
- Paolini Paoletti 2023, pp. 245–246
-
- Dipert 1997, pp. 329–330
- Heil 2009, p. 310
- Heil 2021, 10 Relational Ontology
-
- Heil 2009, p. 311
- Heil 2021, 10.2 Not Nothings but Not Somethings Either
- Marmodoro & Yates 2016, p. 208
- Lupisella 2020, p. 70
- Rickles 2008, p. 24
- Brown & Macpherson 2020, p. 311
-
- Dépelteau 2018, pp. 3–4
- Özekin & Sune 2021, p. 178
-
- Heil 2009, p. 312
- Mulligan 1998, pp. 325–326
- Marmodoro & Yates 2016, p. 36
-
- Heil 2009, p. 312
- Hood 2004, pp. 1–3, 6–7
- Mattingly 2003, p. 41, relation
- Brower 2018, §1. Introduction
-
- Wedin 2002, p. 86
- Skolnik & Berenbaum 2007, Substance And Accident
- Hood 2004, pp. 6–8
-
- Heil 2009, p. 312
- Hood 2004, pp. 1–3, 6–7
- Kim, Sosa & Rosenkrantz 2009, p. 545
- Maspero 2023, pp. 110–112
-
- Mattingly 2003, p. 41, relation
- Brower 2018, lead section, §1. Introduction
- Heil 2009, p. 312
-
- Mattingly 2003, p. 41, relation
- Brower 2018, §1. Introduction
- ^ Brower 2018, §1. Introduction
- Brower 2018, §3.2 Anti-Realism about Relations
- Marmodoro & Yates 2016, p. 40
- Mattingly 2003, p. 42, relation
-
- Borchert 2006, pp. 24–25, Ontology
- Wintgens 2016, p. 42
-
- Borchert 2006, pp. 24–25, Ontology
- Bogen 2005, p. 799
- ^ Mander 2016, pp. 243–244
- Mander 2016, p. 244
- Mander 2016, pp. 244–245
-
- Westerstahl 1989, p. 579
- Verene 2011, p. 8
- Hood 2004, pp. 2–3
- Mulligan 1998, pp. 325–326
- Marmodoro & Yates 2016, p. 37
- Bogen 2005, p. 799
-
- Westerstahl 1989, p. 579
- Verene 2011, p. 8
- Hood 2004, pp. 2–3
- Bogen 2005, p. 799
- Merrill 1990, pp. vii–viii
- Shin 2022, lead section, §1. From Monadic to Polyadic Logic, §2.1 Pragmatic maxim applied to the logic of relations
-
- MacBride 2020, §2. Eliminativism, External Relations and Bradley’s Regress
- Perovic 2017, lead section
- Lærke, Smith & Schliesser 2013, pp. 199–200
-
- Candlish 2016, pp. 16–17
- MacBride 2020, §1. Preliminary Distinctions
-
- Sanford 1980, pp. 69–70
- Armstrong 2010, p. 23
-
- Bogen 2005, p. 798
- Larson 2014, p. 33
-
- Bogen 2005, p. 798
- Shanker 1997, p. 90
- Mácha 2015, p. 58
Sources
- Andrienko, Natalia; Andrienko, Gennady (28 March 2006). Exploratory Analysis of Spatial and Temporal Data: A Systematic Approach. Springer Science & Business Media. ISBN 978-3-540-31190-4.
- Armstrong, David M. (2010). "3. Relations". Sketch for a systematic metaphysics. Clarendon press. ISBN 978-0-19-959061-2.
- Bacon, John B.; Detlefsen, Michael; McCarty, David Charles (5 September 2013). Logic from A to Z: The Routledge Encyclopedia of Philosophy Glossary of Logical and Mathematical Terms. Routledge. ISBN 978-1-134-97097-1.
- Berztiss, A. T. (10 May 2014). Data Structures: Theory and Practice. Academic Press. ISBN 978-1-4832-6472-1.
- Borchert, Donald, ed. (2006). "Ontology". Macmillan Encyclopedia of Philosophy Volume 7 (2 ed.). Macmillan. ISBN 9780028657905.
- Brower, Jeffrey (2018). "Medieval Theories of Relations". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 10 October 2023.
- Brown, Derek H.; Macpherson, Fiona (27 September 2020). The Routledge Handbook of Philosophy of Colour. Routledge. ISBN 978-1-351-04851-4.
- Candlish, Stewart (13 January 2016). The Russell/Bradley Dispute and its Significance for Twentieth Century Philosophy. Springer. ISBN 978-0-230-80061-8.
- Candlish, Stewart; Basile, Pierfrancesco (2023). "Francis Herbert Bradley". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. §6. Metaphysics. Retrieved 10 October 2023.
- Clarke, William Norris (30 November 2015). The One and the Many: A Contemporary Thomistic Metaphysics. University of Notre Dame Press. ISBN 978-0-268-07704-4.
- Clementz, François (2014). "15. Internal, Formal and Thin Relations". In Reboul, Anne (ed.). Mind, values, and metaphysics. 1. Springer. ISBN 978-3-319-04198-8.
- Cowling, Sam (3 February 2017). Abstract Entities. Taylor & Francis. ISBN 978-1-351-97063-1.
- Dainton, Barry (2006). Stream of Consciousness: Unity and Continuity in Conscious Experience. Taylor & Francis. ISBN 978-0-415-37929-8.
- Daly, Christopher (20 July 2010). An Introduction to Philosophical Methods. Broadview Press. ISBN 978-1-55111-934-2.
- Dasgupta, Shamik (September 2015). "Substantivalism vs Relationalism About Space in Classical Physics". Philosophy Compass. 10 (9): 601–624. doi:10.1111/phc3.12219.
- DeLancey, Craig (6 February 2017). A Concise Introduction to Logic. Open Suny Textbooks. ISBN 978-1-942341-43-7.
- Dépelteau, François (10 January 2018). The Palgrave Handbook of Relational Sociology. Springer. ISBN 978-3-319-66005-9.
- Dipert, Randall R. (July 1997). "The Mathematical Structure of the World: The World as Graph". The Journal of Philosophy. 94 (7): 329–358. doi:10.2307/2564553. JSTOR 2564553.
- EB staff (1998). "Logical relation". www.britannica.com. Retrieved 7 October 2023.
- Ehring, Douglas (25 August 2011). Tropes: Properties, Objects, and Mental Causation. OUP. ISBN 978-0-19-960853-9.
- Even, Guy; Medina, Moti (8 October 2012). Digital Logic Design: A Rigorous Approach. Cambridge University Press. ISBN 978-1-139-78979-0.
- Falguera, José L.; Martínez-Vidal, Concha; Rosen, Gideon (2022). "Abstract Objects". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. §3. What is an Abstract Object?. Retrieved 8 October 2023.
- Finster, Felix; Müller, Olaf; Nardmann, Marc; Tolksdorf, Jürgen; Zeidler, Eberhard (8 February 2012). Quantum Field Theory and Gravity: Conceptual and Mathematical Advances in the Search for a Unified Framework. Springer Science & Business Media. ISBN 978-3-0348-0043-3.
- Galluzzo, Gabriele; Loux, Michael J. (16 July 2015). The Problem of Universals in Contemporary Philosophy. Cambridge University Press. ISBN 978-1-107-10089-3.
- Glick, David; Darby, George; Marmodoro, Anna (29 April 2020). The Foundation of Reality: Fundamentality, Space, and Time. Oxford University Press. ISBN 978-0-19-256721-5.
- Gnassounou, Bruno (23 May 2016). Dispositions and Causal Powers. Routledge. ISBN 978-1-317-14950-7.
- Hazlett, A. (30 April 2016). New Waves in Metaphysics. Springer. ISBN 978-0-230-29742-5.
- HC staff (2022). "The American Heritage Dictionary entry: relation". www.ahdictionary.com. HarperCollins Publishers. Retrieved 8 October 2023.
- Heil, John (2009). "Relations". In Le Poidevin, Robin; Peter, Simons; Andrew, McGonigal; Cameron, Ross P. (eds.). The Routledge Companion to Metaphysics. Routledge. pp. 310–321. doi:10.4324/9780203879306-34. ISBN 978-0-203-87930-6.
- Heil, John Fergusson (2021). Relations. Cambridge University Press. ISBN 978-1-108-94061-0.
- Hoad, T. F. (1993). The concise Oxford dictionary of english etymology. Oxford University Press. ISBN 0-19-283098-8.
- Holzhey, Helmut; Mudroch, Vilem (2005). Historical Dictionary of Kant and Kantianism. Scarecrow Press. ISBN 0-8108-5390-6.
- Bogen, James (2005). Honderich, Ted (ed.). The Oxford Companion to Philosophy. Oxford University Press. ISBN 9780199264797.
- Hood, Pamela Michelle (2004). Aristotle on the Category of Relation. University Press of America. ISBN 978-0-7618-3007-8.
- Joad, C. E. M. (January 1929). "The One and the Many". Philosophy. 4 (13): 87–100. doi:10.1017/S0031819100031120. S2CID 145730575.
- Kim, Jaegwon; Sosa, Ernest; Rosenkrantz, Gary S. (2009). A companion to metaphysics (2nd ed.). Wiley-Blackwell. ISBN 978-1-405-15298-3.
- Koons, Robert C.; Pickavance, Timothy H. (2017). The atlas of reality: a comprehensive guide to metaphysics. Wiley Blackwell. ISBN 9781119116127.
- Ladyman, James (2023). "Structural Realism". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. §4. Ontic Structural Realism (OSR). Retrieved 3 October 2023.
- Lærke, Mogens; Smith, Justin E. H.; Schliesser, Eric (14 June 2013). Philosophy and Its History: Aims and Methods in the Study of Early Modern Philosophy. Oxford University Press. ISBN 978-0-19-985715-9.
- Larson, Richard K. (3 February 2014). On Shell Structure. Routledge. ISBN 978-1-134-11382-8.
- Le Poidevin, Robin; Peter, Simons; Andrew, McGonigal; Cameron, Ross P., eds. (2009). The Routledge Companion to Metaphysics. Routledge. ISBN 978-0-203-87930-6.
- Levich, A. P. (1996). On the Way to Understanding the Time Phenomenon: The Constructions of Time in Natural Science. World Scientific. ISBN 978-981-02-1606-1.
- Lewis, David (13 January 1999). Papers in Metaphysics and Epistemology: Volume 2. Cambridge University Press. ISBN 978-0-521-58787-7.
- Loux, Michael J.; Zimmerman, Dean W. (8 September 2005). The Oxford Handbook of Metaphysics. OUP Oxford. ISBN 978-0-19-928422-1.
- Lupisella, Mark (21 July 2020). Cosmological Theories of Value: Science, Philosophy, and Meaning in Cosmic Evolution. Springer Nature. ISBN 978-3-030-25339-4.
- Lyons, John (2 June 1977). Semantics: Volume 1. Cambridge University Press. ISBN 978-0-521-29165-1.
- MacBride, Fraser (March 2007). "Neutral Relations Revisited". Dialectica. 61 (1): 25–56. doi:10.1111/j.1746-8361.2007.01092.x.
- MacBride, Fraser (2 March 2018). On the Genealogy of Universals: The Metaphysical Origins of Analytic Philosophy. Oxford University Press. ISBN 978-0-19-253930-4.
- MacBride, Fraser (2020). "Relations". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 5 October 2023.
- Mácha, Jakub (21 May 2015). Wittgenstein on Internal and External Relations: Tracing all the Connections. Bloomsbury Publishing. ISBN 978-1-4742-4213-4.
- Makridis, Odysseus (2022). Symbolic Logic. Palgrave Macmillan. ISBN 978-3-030-67396-3.
- Mander, W. J. (2016). Idealist Ethics. Oxford University Press. ISBN 978-0-19-874889-2.
- Marmodoro, Anna; Yates, David, eds. (2016). The metaphysics of relations. Oxford university press. ISBN 9780198735878.
- Maspero, Giulio (31 December 2023). The Cappadocian Reshaping of Metaphysics: Relational Being. Cambridge University Press. ISBN 978-1-009-41206-3.
- Mattingly, B. (2003). "relation". New Catholic Encyclopedia (2 ed.). Thompson/Gale Catholic university of America. ISBN 0-7876-4016-6.
- Maurin, A.-S. (17 April 2013). If Tropes. Springer Science & Business Media. ISBN 978-94-017-0079-5.
- McKeon, Matthew. "Logical Consequence". Internet Encyclopedia of Philosophy. Retrieved 7 October 2023.
- Merrill, Daniel D. (1990). Augustus de Morgan and the logic of relations. Kluwer Acad. Publ. ISBN 9780792307587.
- Monnoyer, Jean-Maurice (2 May 2013). Metaphysics and Truthmakers. Walter de Gruyter. ISBN 978-3-11-032691-8.
- Mulligan, Kevin (1998). "Relations: Through Thick and Thin". Erkenntnis. 48 (2/3): 325–353. doi:10.1023/a:1005454805376.
- Mumford, Stephen (2 August 2004). Laws in Nature. Routledge. ISBN 978-1-134-38651-2.
- MW staff. "Definition of Relata". www.merriam-webster.com. Retrieved 8 October 2023.
- MW staff (6 October 2023). "Definition of Relationship". www.merriam-webster.com. Retrieved 8 October 2023.
- Orilia, Francesco; Paolini Paoletti, Michele (2022). "Properties". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. §1.5 Relations. Retrieved 8 October 2023.
- Özekin, M. Kürşad; Sune, Engin, eds. (29 November 2021). Critical Approaches to International Relations: Philosophical Foundations and Current Debates. BRILL. ISBN 978-90-04-47050-7.
- Paolini Paoletti, Michele (June 2023). "Relationism and the Problem of Order". Acta Analytica. 38 (2): 245–273. doi:10.1007/s12136-022-00513-4. S2CID 247432632.
- Papineau, David (4 October 2012). Philosophical Devices: Proofs, Probabilities, Possibilities, and Sets. Oxford University Press. ISBN 978-0-19-965172-6.
- Parry, William T.; Hacker, Edward A. (3 September 1991). Aristotelian Logic. State University of New York Press. ISBN 978-1-4384-1557-4.
- Patard, Adeline; Brisard, Frank (2011). Cognitive Approaches to Tense, Aspect, and Epistemic Modality. John Benjamins Publishing. ISBN 978-90-272-2383-8.
- Perovic, Katarina (2017). "Bradley's Regress". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 10 October 2023.
- Piaget, Jean (22 January 2002). Judgement and Reasoning in the Child. Routledge. ISBN 978-1-134-61785-2.
- Porcu, Emilio; Montero, José-María; Schlather, Martin (5 January 2012). Advances and Challenges in Space-time Modelling of Natural Events. Springer Science & Business Media. ISBN 978-3-642-17086-7.
- Rickabaugh, Brandon; Moreland, J. P. (24 October 2023). The Substance of Consciousness: A Comprehensive Defense of Contemporary Substance Dualism. John Wiley & Sons. ISBN 978-1-394-19548-0.
- Rickles, Dean (2008). Symmetry, Structure, and Spacetime. Elsevier. ISBN 978-0-444-53116-2.
- Runggaldier, Edmund (2009). Unity and Time in Metaphysics. Walter de Gruyter. ISBN 978-3-11-021234-1.
- Sanford, David H. (1980). "Armstrong's Theory of Universals". The British Journal for the Philosophy of Science. 31 (1): 69–79. doi:10.1093/bjps/31.1.69. ISSN 0007-0882. JSTOR 687253.
- Shanker, V. A. (1997). Ludwig Wittgenstein: Critical Assessments. Taylor & Francis. ISBN 978-0-415-14947-1.
- Shin, Sun-Joo (2022). "Peirce's Deductive Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 12 October 2023.
- Sider, Theodore (2010). Logic for Philosophy. Oxford University Press. ISBN 978-0-19-957559-6.
- Skolnik, Fred; Berenbaum, Michael, eds. (2007). "Substance And Accident". Encyclopaedia judaica (2nd ed.). Thomson Gale. ISBN 978-0028659282.
- Szatkowski, Miroslaw (18 March 2022). E.J. Lowe and Ontology. Routledge. ISBN 978-1-000-55385-7.
- Thomasson, Amie. "Categories". Stanford Encyclopedia of Philosophy. Stanford University. §1.2 Kantian Conceptualism. Retrieved 16 October 2023.
- Thompson, Della (2000). "Relation". The Pocket Oxford Dictionary of Current English. Oxford University Press. ISBN 978-0-19-860345-0.
- Trautwein, Martin (22 December 2011). The Time Window of Language: The Interaction between Linguistic and Non-Linguistic Knowledge in the Temporal Interpretation of German and English Texts. Walter de Gruyter. ISBN 978-3-11-091952-3.
- Turetzky, Philip (11 April 2019). The Elements of Arguments: An Introduction to Critical Thinking and Logic. Broadview Press. ISBN 978-1-4604-0646-5.
- Verene, Donald Phillip (30 December 2011). The Origins of the Philosophy of Symbolic Forms: Kant, Hegel, and Cassirer. Northwestern University Press. ISBN 978-0-8101-2778-4.
- Wallis, W. D. (2003). A Beginner's Guide to Discrete Mathematics. Springer Science & Business Media. ISBN 978-0-8176-4269-3.
- Wardy, Robert (1998). "Categories: 3. Categories in Kant". Routledge Encyclopedia of Philosophy. Routledge. Retrieved 16 October 2023.
- Wedin, Michael Vernon (2002). Aristotle's Theory of Substance: The Categories and Metaphysics Zeta. Oxford University Press. ISBN 978-0-19-925308-1.
- Westerstahl, Dag (December 1989). "Aristotelian syllogisms and generalized quantifiers". Studia Logica. 48 (4): 577–585. doi:10.1007/bf00370209. S2CID 32089424.
- Wintgens, Luc J. (22 April 2016). Legisprudence: Practical Reason in Legislation. Routledge. ISBN 978-1-317-10591-6.