| Lie groups and Lie algebras | ||||
|---|---|---|---|---|
 | ||||
Classical groups
|
||||
Simple Lie groups
|
||||
| Other Lie groups | ||||
| Lie algebras | ||||
| Semisimple Lie algebra | ||||
| Representation theory | ||||
| Lie groups in physics | ||||
| Scientists | ||||
In mathematics, the representation theory of semisimple Lie algebras is one of the crowning achievements of the theory of Lie groups and Lie algebras. The theory was worked out mainly by E. Cartan and H. Weyl and because of that, the theory is also known as the Cartan–Weyl theory. The theory gives the structural description and classification of a finite-dimensional representation of a semisimple Lie algebra (over ); in particular, it gives a way to parametrize (or classify) irreducible finite-dimensional representations of a semisimple Lie algebra, the result known as the theorem of the highest weight.
There is a natural one-to-one correspondence between the finite-dimensional representations of a simply connected compact Lie group K and the finite-dimensional representations of the complex semisimple Lie algebra that is the complexification of the Lie algebra of K (this fact is essentially a special case of the Lie group–Lie algebra correspondence). Also, finite-dimensional representations of a connected compact Lie group can be studied through finite-dimensional representations of the universal cover of such a group. Hence, the representation theory of semisimple Lie algebras marks the starting point for the general theory of representations of connected compact Lie groups.
The theory is a basis for the later works of Harish-Chandra that concern (infinite-dimensional) representation theory of real reductive groups.
Classifying finite-dimensional representations of semisimple Lie algebras
See also: Weight (representation theory) § Weights in the representation theory of semisimple Lie algebras, and Theorem on the highest weightsThere is a beautiful theory classifying the finite-dimensional representations of a semisimple Lie algebra over . The finite-dimensional irreducible representations are described by a theorem of the highest weight. The theory is described in various textbooks, including Fulton & Harris (1991), Hall (2015), and Humphreys (1972).
Following an overview, the theory is described in increasing generality, starting with two simple cases that can be done "by hand" and then proceeding to the general result. The emphasis here is on the representation theory; for the geometric structures involving root systems needed to define the term "dominant integral element," follow the above link on weights in representation theory.
Overview
Classification of the finite-dimensional irreducible representations of a semisimple Lie algebra over or generally consists of two steps. The first step amounts to analysis of hypothesized representations resulting in a tentative classification. The second step is actual realization of these representations.
A real Lie algebra is usually complexified enabling analysis in an algebraically closed field. Working over the complex numbers in addition admits nicer bases. The following theorem applies: A real-linear finite-dimensional representation of a real Lie algebra extends to a complex-linear representation of its complexification. The real-linear representation is irreducible if and only if the corresponding complex-linear representation is irreducible. Moreover, a complex semisimple Lie algebra has the complete reducibility property. This means that every finite-dimensional representation decomposes as a direct sum of irreducible representations.
- Conclusion: Classification amounts to studying irreducible complex linear representations of the (complexified) Lie algebra.
Classification: Step One
The first step is to hypothesize the existence of irreducible representations. That is to say, one hypothesizes that one has an irreducible representation of a complex semisimple Lie algebra without worrying about how the representation is constructed. The properties of these hypothetical representations are investigated, and conditions necessary for the existence of an irreducible representation are then established.
The properties involve the weights of the representation. Here is the simplest description. Let be a Cartan subalgebra of , that is a maximal commutative subalgebra with the property that is diagonalizable for each , and let be a basis for . A weight for a representation of is a collection of simultaneous eigenvalues
for the commuting operators . In basis-independent language, is a linear functional on such that there exists a nonzero vector such that for every .
A partial ordering on the set of weights is defined, and the notion of highest weight in terms of this partial ordering is established for any set of weights. Using the structure on the Lie algebra, the notions dominant element and integral element are defined. Every finite-dimensional representation must have a maximal weight , i.e., one for which no strictly higher weight occurs. If is irreducible and is a weight vector with weight , then the entire space must be generated by the action of on . Thus, is a "highest weight cyclic" representation. One then shows that the weight is actually the highest weight (not just maximal) and that every highest weight cyclic representation is irreducible. One then shows that two irreducible representations with the same highest weight are isomorphic. Finally, one shows that the highest weight must be dominant and integral.
- Conclusion: Irreducible representations are classified by their highest weights, and the highest weight is always a dominant integral element.
Step One has the side benefit that the structure of the irreducible representations is better understood. Representations decompose as direct sums of weight spaces, with the weight space corresponding to the highest weight one-dimensional. Repeated application of the representatives of certain elements of the Lie algebra called lowering operators yields a set of generators for the representation as a vector space. The application of one such operator on a vector with definite weight results either in zero or a vector with strictly lower weight. Raising operators work similarly, but results in a vector with strictly higher weight or zero. The representatives of the Cartan subalgebra acts diagonally in a basis of weight vectors.
Classification: Step Two
Step Two is concerned with constructing the representations that Step One allows for. That is to say, we now fix a dominant integral element and try to construct an irreducible representation with highest weight .
There are several standard ways of constructing irreducible representations:
- Construction using Verma modules. This approach is purely Lie algebraic. (Generally applicable to complex semisimple Lie algebras.)
- The compact group approach using the Peter–Weyl theorem. If, for example, , one would work with the simply connected compact group . (Generally applicable to complex semisimple Lie algebras.)
- Construction using the Borel–Weil theorem, in which holomorphic representations of the group G corresponding to are constructed. (Generally applicable to complex semisimple Lie algebras.)
- Performing standard operations on known representations, in particular applying Clebsch–Gordan decomposition to tensor products of representations. (Not generally applicable.) In the case , this construction is described below.
- In the simplest cases, construction from scratch.
- Conclusion: Every dominant integral element of a complex semisimple Lie algebra gives rise to an irreducible, finite-dimensional representation. These are the only irreducible representations.
The case of sl(2,C)
See also: Special linear Lie algebra and Representation theory of SU(2)The Lie algebra sl(2,C) of the special linear group SL(2,C) is the space of 2x2 trace-zero matrices with complex entries. The following elements form a basis:
These satisfy the commutation relations
- .
Every finite-dimensional representation of sl(2,C) decomposes as a direct sum of irreducible representations. This claim follows from the general result on complete reducibility of semisimple Lie algebras, or from the fact that sl(2,C) is the complexification of the Lie algebra of the simply connected compact group SU(2). The irreducible representations , in turn, can be classified by the largest eigenvalue of , which must be a non-negative integer m. That is to say, in this case, a "dominant integral element" is simply a non-negative integer. The irreducible representation with largest eigenvalue m has dimension and is spanned by eigenvectors for with eigenvalues . The operators and move up and down the chain of eigenvectors, respectively. This analysis is described in detail in the representation theory of SU(2) (from the point of the view of the complexified Lie algebra).
One can give a concrete realization of the representations (Step Two in the overview above) in either of two ways. First, in this simple example, it is not hard to write down an explicit basis for the representation and an explicit formula for how the generators of the Lie algebra act on this basis. Alternatively, one can realize the representation with highest weight by letting denote the space of homogeneous polynomials of degree in two complex variables, and then defining the action of , , and by
Note that the formulas for the action of , , and do not depend on ; the subscript in the formulas merely indicates that we are restricting the action of the indicated operators to the space of homogeneous polynomials of degree in and .
The case of sl(3,C)
See also: Clebsch–Gordan coefficients for SU(3)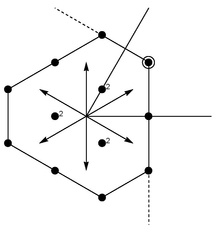

There is a similar theory classifying the irreducible representations of sl(3,C), which is the complexified Lie algebra of the group SU(3). The Lie algebra sl(3,C) is eight dimensional. We may work with a basis consisting of the following two diagonal elements
- ,
together with six other matrices and each of which has a 1 in an off-diagonal entry and zeros elsewhere. (The 's have a 1 above the diagonal and the 's have a 1 below the diagonal.)
The strategy is then to simultaneously diagonalize and in each irreducible representation . Recall that in the sl(2,C) case, the action of and raise and lower the eigenvalues of . Similarly, in the sl(3,C) case, the action of and "raise" and "lower" the eigenvalues of and . The irreducible representations are then classified by the largest eigenvalues and of and , respectively, where and are non-negative integers. That is to say, in this setting, a "dominant integral element" is precisely a pair of non-negative integers.
Unlike the representations of sl(2,C), the representation of sl(3,C) cannot be described explicitly in general. Thus, it requires an argument to show that every pair actually arises the highest weight of some irreducible representation (Step Two in the overview above). This can be done as follows. First, we construct the "fundamental representations", with highest weights (1,0) and (0,1). These are the three-dimensional standard representation (in which ) and the dual of the standard representation. Then one takes a tensor product of copies of the standard representation and copies of the dual of the standard representation, and extracts an irreducible invariant subspace.
Although the representations cannot be described explicitly, there is a lot of useful information describing their structure. For example, the dimension of the irreducible representation with highest weight is given by
There is also a simple pattern to the multiplicities of the various weight spaces. Finally, the irreducible representations with highest weight can be realized concretely on the space of homogeneous polynomials of degree in three complex variables.
The case of a general semisimple Lie algebras
Main article: Theorem of the highest weight See also: Compact group § Representation theory of a connected compact Lie groupLet be a semisimple Lie algebra and let be a Cartan subalgebra of , that is, a maximal commutative subalgebra with the property that adH is diagonalizable for all H in . As an example, we may consider the case where is sl(n,C), the algebra of n by n traceless matrices, and is the subalgebra of traceless diagonal matrices. We then let R denote the associated root system. We then choose a base (or system of positive simple roots) for R.
We now briefly summarize the structures needed to state the theorem of the highest weight; more details can be found in the article on weights in representation theory. We choose an inner product on that is invariant under the action of the Weyl group of R, which we use to identify with its dual space. If is a representation of , we define a weight of V to be an element in with the property that for some nonzero v in V, we have for all H in . We then define one weight to be higher than another weight if is expressible as a linear combination of elements of with non-negative real coefficients. A weight is called a highest weight if is higher than every other weight of . Finally, if is a weight, we say that is dominant if it has non-negative inner product with each element of and we say that is integral if is an integer for each in R.
Finite-dimensional representations of a semisimple Lie algebra are completely reducible, so it suffices to classify irreducible (simple) representations. The irreducible representations, in turn, may be classified by the "theorem of the highest weight" as follows:
- Every irreducible, finite-dimensional representation of has a highest weight, and this highest weight is dominant and integral.
- Two irreducible, finite-dimensional representations with the same highest weight are isomorphic.
- Every dominant integral element arises as the highest weight of some irreducible, finite-dimensional representation of .
The last point of the theorem (Step Two in the overview above) is the most difficult one. In the case of the Lie algebra sl(3,C), the construction can be done in an elementary way, as described above. In general, the construction of the representations may be given by using Verma modules.
Construction using Verma modules
If is any weight, not necessarily dominant or integral, one can construct an infinite-dimensional representation of with highest weight known as a Verma module. The Verma module then has a maximal proper invariant subspace , so that the quotient representation is irreducible—and still has highest weight . In the case that is dominant and integral, we wish to show that is finite dimensional.
The strategy for proving finite-dimensionality of is to show that the set of weights of is invariant under the action of the Weyl group of relative to the given Cartan subalgebra . (Note that the weights of the Verma module itself are definitely not invariant under .) Once this invariance result is established, it follows that has only finitely many weights. After all, if is a weight of , then must be integral—indeed, must differ from by an integer combination of roots—and by the invariance result, must be lower than for every in . But there are only finitely many integral elements with this property. Thus, has only finitely many weights, each of which has finite multiplicity (even in the Verma module, so certainly also in ). From this, it follows that must be finite dimensional.
Additional properties of the representations
Much is known about the representations of a complex semisimple Lie algebra , besides the classification in terms of highest weights. We mention a few of these briefly. We have already alluded to Weyl's theorem, which states that every finite-dimensional representation of decomposes as a direct sum of irreducible representations. There is also the Weyl character formula, which leads to the Weyl dimension formula (a formula for the dimension of the representation in terms of its highest weight), the Kostant multiplicity formula (a formula for the multiplicities of the various weights occurring in a representation). Finally, there is also a formula for the eigenvalue of the Casimir element, which acts as a scalar in each irreducible representation.
Lie group representations and Weyl's unitarian trick
Although it is possible to develop the representation theory of complex semisimple Lie algebras in a self-contained way, it can be illuminating to bring in a perspective using Lie groups. This approach is particularly helpful in understanding Weyl's theorem on complete reducibility. It is known that every complex semisimple Lie algebra has a compact real form . This means first that is the complexification of :
and second that there exists a simply connected compact group whose Lie algebra is . As an example, we may consider , in which case may be taken to be the special unitary group SU(n).
Given a finite-dimensional representation of , we can restrict it to . Then since is simply connected, we can integrate the representation to the group . The method of averaging over the group shows that there is an inner product on that is invariant under the action of ; that is, the action of on is unitary. At this point, we may use unitarity to see that decomposes as a direct sum of irreducible representations. This line of reasoning is called the unitarian trick and was Weyl's original argument for what is now called Weyl's theorem. There is also a purely algebraic argument for the complete reducibility of representations of semisimple Lie algebras.
If is a complex semisimple Lie algebra, there is a unique complex semisimple Lie group with Lie algebra , in addition to the simply connected compact group . (If then .) Then we have the following result about finite-dimensional representations.
Statement: The objects in the following list are in one-to-one correspondence:
- Smooth representations of K
- Holomorphic representations of G
- Real linear representations of
- Complex linear representations of
- Conclusion: The representation theory of compact Lie groups can shed light on the representation theory of complex semisimple Lie algebras.
Remarks
- This approach is used heavily for classical Lie algebras in Fulton & Harris (1991).
Notes
- Knapp, A. W. (2003). "Reviewed work: Matrix Groups: An Introduction to Lie Group Theory, Andrew Baker; Lie Groups: An Introduction through Linear Groups, Wulf Rossmann". The American Mathematical Monthly. 110 (5): 446–455. doi:10.2307/3647845. JSTOR 3647845.
- Hall 2015, Proposition 4.6.
- See Section 6.4 of Hall 2015 in the case of sl(3,C)
- Hall 2015, Section 6.2. (There specialized to )
- Hall 2015, Section 7.2.
- Bäuerle, de Kerf & ten Kroode 1997, Chapter 20.
- Hall 2015, Sections 9.5–9.7
- Hall 2015, Chapter 12.
- ^ Rossmann 2002, Chapter 6.
- This approach for can be found in Example 4.10. of Hall (2015, Section 4.2.)
- Hall 2015 Section 10.3
- Hall 2015 Theorems 4.28 and 5.6
- Hall 2015 Section 4.6
- Hall 2015 Equation 4.16
- Hall 2015 Example 4.10
- Hall 2015 Chapter 6
- Hall 2015 Theorem 6.7
- Hall 2015 Proposition 6.17
- Hall 2015 Theorem 6.27
- Hall 2015 Exercise 6.8
- Hall 2015 Section 7.7.1
- Hall 2015 Theorems 9.4 and 9.5
- Hall 2015 Sections 9.5-9.7
- Hall 2015 Section 9.7
- Hall 2015 Proposition 9.22
- Knapp 2002 Section VI.1
- Hall 2015 Theorem 5.6
- Hall 2015 Section 4.4
- Knapp 2001, Section 2.3.
References
- Bäuerle, G. G. A.; de Kerf, E. A.; ten Kroode, A. P. E. (1997). A. van Groesen; E.M. de Jager (eds.). Finite and infinite dimensional Lie algebras and their application in physics. Studies in mathematical physics. Vol. 7. North-Holland. ISBN 978-0-444-82836-1 – via ScienceDirect.
- Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. Vol. 129. New York: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.
- Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, vol. 222 (2nd ed.), Springer, ISBN 978-3319134666
- Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90053-7
- Knapp, Anthony W. (2001), Representation theory of semisimple groups. An overview based on examples., Princeton Landmarks in Mathematics, Princeton University Press, ISBN 0-691-09089-0
- Knapp, Anthony W. (2002), Lie Groups: Beyond an Introduction, Progress in Mathematics, vol. 140 (2nd ed.), Boston: Birkhäuser, ISBN 978-0-8176-4259-4.
- Rossmann, Wulf (2002), Lie Groups: An Introduction Through Linear Groups, Oxford Graduate Texts in Mathematics, Oxford University Press, ISBN 978-0-19-859683-7.
 ); in particular, it gives a way to parametrize (or classify) irreducible finite-dimensional representations of a semisimple Lie algebra, the result known as the
); in particular, it gives a way to parametrize (or classify) irreducible finite-dimensional representations of a semisimple Lie algebra, the result known as the  that is the complexification of the Lie algebra of K (this fact is essentially a special case of the
that is the complexification of the Lie algebra of K (this fact is essentially a special case of the  or
or  of a complex semisimple Lie algebra
of a complex semisimple Lie algebra  without worrying about how the representation is constructed. The properties of these hypothetical representations are investigated, and conditions necessary for the existence of an irreducible representation are then established.
without worrying about how the representation is constructed. The properties of these hypothetical representations are investigated, and conditions necessary for the existence of an irreducible representation are then established.
 be a Cartan subalgebra of
be a Cartan subalgebra of  is diagonalizable for each
is diagonalizable for each  , and let
, and let  be a basis for
be a basis for  for a representation
for a representation  of
of 
 . In basis-independent language,
. In basis-independent language,  such that
such that  for every
for every  is irreducible and
is irreducible and  is a weight vector with weight
is a weight vector with weight  , one would work with the simply connected compact group
, one would work with the simply connected compact group  . (Generally applicable to complex semisimple Lie algebras.)
. (Generally applicable to complex semisimple Lie algebras.) , this construction is described below.
, this construction is described below.
 .
. , which must be a non-negative integer m. That is to say, in this case, a "dominant integral element" is simply a non-negative integer.
The irreducible representation with largest eigenvalue m has dimension
, which must be a non-negative integer m. That is to say, in this case, a "dominant integral element" is simply a non-negative integer.
The irreducible representation with largest eigenvalue m has dimension  and is spanned by eigenvectors for
and is spanned by eigenvectors for  . The operators
. The operators  and
and  move up and down the chain of eigenvectors, respectively. This analysis is described in detail in the
move up and down the chain of eigenvectors, respectively. This analysis is described in detail in the  of the Lie algebra act on this basis. Alternatively, one can realize the representation with highest weight
of the Lie algebra act on this basis. Alternatively, one can realize the representation with highest weight  by letting
by letting  denote the space of homogeneous polynomials of degree
denote the space of homogeneous polynomials of degree  ,
,  , and
, and  by
by

 and
and  .
.
 ,
, and
and  each of which has a 1 in an off-diagonal entry and zeros elsewhere. (The
each of which has a 1 in an off-diagonal entry and zeros elsewhere. (The  's have a 1 above the diagonal and the
's have a 1 above the diagonal and the  's have a 1 below the diagonal.)
's have a 1 below the diagonal.)
 and
and  in each irreducible representation
in each irreducible representation  and
and  "raise" and "lower" the eigenvalues of
"raise" and "lower" the eigenvalues of  and
and  of
of  actually arises the highest weight of some irreducible representation (Step Two in the overview above). This can be done as follows. First, we construct the "fundamental representations", with highest weights (1,0) and (0,1). These are the three-dimensional standard representation (in which
actually arises the highest weight of some irreducible representation (Step Two in the overview above). This can be done as follows. First, we construct the "fundamental representations", with highest weights (1,0) and (0,1). These are the three-dimensional standard representation (in which  ) and the dual of the standard representation. Then one takes a tensor product of
) and the dual of the standard representation. Then one takes a tensor product of 
 can be realized concretely on the space of homogeneous polynomials of degree
can be realized concretely on the space of homogeneous polynomials of degree  for R.
for R.
 for all H in
for all H in  if
if  is expressible as a linear combination of elements of
is expressible as a linear combination of elements of  is an integer for each
is an integer for each  in R.
in R.
 of
of  , so that the
, so that the  is irreducible—and still has highest weight
is irreducible—and still has highest weight  is finite dimensional.
is finite dimensional.
 of
of  must be lower than
must be lower than  in
in  . This means first that
. This means first that 
 whose Lie algebra is
whose Lie algebra is  , in which case
, in which case  with Lie algebra
with Lie algebra  .) Then we have the following result about finite-dimensional representations.
.) Then we have the following result about finite-dimensional representations.
 )
)
 can be found in Example 4.10. of
can be found in Example 4.10. of