Minimal surface in differential geometry
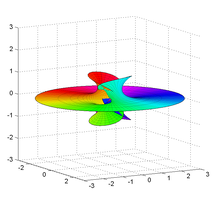
Richmond surface for m=2. In differential geometry , a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. It is a family of surfaces with one planar end and one Enneper surface -like self-intersecting end.
It has Weierstrass–Enneper parameterization
f
(
z
)
=
1
/
z
2
,
g
(
z
)
=
z
m
{\displaystyle f(z)=1/z^{2},g(z)=z^{m}}
X
(
z
)
=
ℜ
[
(
−
1
/
2
z
)
−
z
2
m
+
1
/
(
4
m
+
2
)
]
Y
(
z
)
=
ℜ
[
(
−
i
/
2
z
)
+
i
z
2
m
+
1
/
(
4
m
+
2
)
]
Z
(
z
)
=
ℜ
[
z
m
/
m
]
{\displaystyle {\begin{aligned}X(z)&=\Re \\Y(z)&=\Re \\Z(z)&=\Re \end{aligned}}}
The associate family of the surface is just the surface rotated around the z-axis.
Taking m = 2 a real parametric expression becomes:
X
(
u
,
v
)
=
(
1
/
3
)
u
3
−
u
v
2
+
u
u
2
+
v
2
Y
(
u
,
v
)
=
−
u
2
v
+
(
1
/
3
)
v
3
−
v
u
2
+
v
2
Z
(
u
,
v
)
=
2
u
{\displaystyle {\begin{aligned}X(u,v)&=(1/3)u^{3}-uv^{2}+{\frac {u}{u^{2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3}-{\frac {v}{u^{2}+v^{2}}}\\Z(u,v)&=2u\end{aligned}}}
References
Jesse Douglas , Tibor Radó, The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó, World Scientific, 1992 (p. 239-240)
See also
Category :
Text is available under the Creative Commons Attribution-ShareAlike License. Additional terms may apply.
**DISCLAIMER** We are not affiliated with Wikipedia, and Cloudflare.
The information presented on this site is for general informational purposes only and does not constitute medical advice.
You should always have a personal consultation with a healthcare professional before making changes to your diet, medication, or exercise routine.
AI helps with the correspondence in our chat.
We participate in an affiliate program. If you buy something through a link, we may earn a commission 💕
↑

 . This allows a parametrization based on a complex parameter as
. This allows a parametrization based on a complex parameter as

