
The Shapley–Folkman lemma is a result in convex geometry that describes the Minkowski addition of sets in a vector space. It is named after mathematicians Lloyd Shapley and Jon Folkman, but was first published by the economist Ross M. Starr.
The lemma may be intuitively understood as saying that, if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.
Related results provide more refined statements about how close the approximation is. For example, the Shapley–Folkman theorem provides an upper bound on the distance between any point in the Minkowski sum and its convex hull. This upper bound is sharpened by the Shapley–Folkman–Starr theorem (alternatively, Starr's corollary).
The Shapley–Folkman lemma has applications in economics, optimization and probability theory. In economics, it can be used to extend results proved for convex preferences to non-convex preferences. In optimization theory, it can be used to explain the successful solution of minimization problems that are sums of many functions. In probability, it can be used to prove a law of large numbers for random sets.
Introductory example
A set is convex if every line segment joining two of its points is a subset in the set: For example, the solid disk is a convex set but the circle is not, because the line segment joining two distinct points is not a subset of the circle.
The convex hull of a set Q is the smallest convex set that contains Q. This distance is zero if and only if the sum is convex.
Minkowski addition is the addition of the set members. For example, adding the set consisting of the integers zero and one to itself yields the set consisting of zero, one, and two:The subset of the integers {0,1,2} is contained in the interval of real numbers , which is convex. The Shapley–Folkman lemma implies that every point in is the sum of an integer from {0,1} and a real number from .
The distance between the convex interval and the non-convex set {0,1,2} equals one-half:
However, the distance between the average Minkowski sum
and its convex hull is only 1/4, which is half the distance (1/2) between its summand {0,1} and . As more sets are added together, the average of their sum "fills out" its convex hull: The maximum distance between the average and its convex hull approaches zero as the average includes more summands.
Preliminaries
The Shapley–Folkman lemma depends upon the following definitions and results from convex geometry.
Real vector spaces
A real vector space of two dimensions can be given a Cartesian coordinate system in which every point is identified by an ordered pair of real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise:
further, a point can be multiplied by each real number λ coordinate-wise:
More generally, any real vector space of (finite) dimension D can be viewed as the set of all D-tuples of D real numbers {(v1, v2, …, vD)} on which two operations are defined: vector addition and multiplication by a real number. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.
Convex sets
 In a convex set Q, the line segment connecting any two of its points is a subset of Q.
In a convex set Q, the line segment connecting any two of its points is a subset of Q. In a non-convex set Q, a point in some line-segment joining two of its points is not a member of Q.Line segments test whether a subset be convex.
In a non-convex set Q, a point in some line-segment joining two of its points is not a member of Q.Line segments test whether a subset be convex.
In a real vector space, a non-empty set Q is defined to be convex if, for each pair of its points, every point on the line segment that joins them is still in Q. For example, a solid disk is convex but a circle is not, because it does not contain a line segment joining its points ; the non-convex set of three integers {0,1,2} is contained in the interval , which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent shape, is non-convex. The empty set is convex, either by definition or vacuously, depending on the author.
More formally, a set Q is convex if, for all points v1and v2 in Q and for every real number λ in the unit interval , the point
is a member of Q.
By mathematical induction, a set Q is convex if and only if every convex combination of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v1, v2, …, vD} of a vector space is any weighted average λ1v1 + λ2v2 + … + λDvD for some indexed set of non-negative real numbers {λd} satisfying the equation λ0 + λ1 + … + λD = 1.
The definition of a convex set implies that the intersection of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.
Convex hull

For every subset Q of a real vector space, its convex hull Conv(Q) is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q. The convex hull of a set can be equivalently defined to be the set of all convex combinations of points in Q. For example, the convex hull of the set of integers {0,1} is the closed interval of real numbers , which contains the integer end-points. The convex hull of the unit circle is the closed unit disk, which contains the unit circle.
Minkowski addition

In any vector space (or algebraic structure with addition), X, the Minkowski sum of two non-empty sets A,B ⊆ X is defined to be the element-wise operation A + B = {x + y | x ∈ A, y ∈ B} (See also .) For example,
This operation is clearly commutative and associative on the collection of non-empty sets. All such operations extend in a well-defined manner to recursive forms By the principle of induction it is easy to see that
Convex hulls of Minkowski sums
Minkowski addition behaves well with respect to taking convex hulls. Specifically, for all subsets A,B ⊆ X of a real vector space, X, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls. That is,
And by induction it follows that
for any N ∈ ℕ and non-empty subsets Qn ⊆ X, 1 ≤ n ≤ N.
Statements of the three main results
Notation
D and N represent positive integers. D is the dimension of the ambient space ℝ.
Q1, …, QN are nonempty, bounded subsets of ℝ. They are also called "summands". N is the number of summands.
is the Minkowski sum of the summands.
x represents an arbitrary vector in Conv(Q).
Shapley–Folkman lemma
Since , for any x ∈ Conv(Q), there exist elements qn ∈ Conv(Qn) such that . The Shapley–Folkman lemma refines this statement.
Shapley–Folkman lemma — For any x ∈ Conv(Q), there exist elements qn such that , and at most D of the summands qn ∈ Conv(Qn) \ Qn, while the others qn ∈ Qn.
For example, every point in = + = Conv({0,1}) + Conv({0,1}) is the sum of an element in {0,1} and an element in .
Shuffling indices if necessary, this means that every point in Conv(Q) can be decomposed as
where qn ∈ Conv(Qn) for 1 ≤ n ≤ D and qn ∈ Qn for D + 1 ≤ n ≤ N. Note that the reindexing depends on the point x.
The lemma may be stated succinctly as
The converse of Shapley–Folkman lemma
converse of Shapley–Folkman lemma — If a vector space obeys the Shapley–Folkman lemma for a natural number D, and for no number less than D, then its dimension is finite, and exactly D.
In particular, the Shapley–Folkman lemma requires the vector space to be finite-dimensional.
Shapley–Folkman theorem
Shapley and Folkman used their lemma to prove the following theorem, which quantifies the difference between Q and Conv(Q) using squared Euclidean distance.
For any nonempty subset and any point define their squared Euclidean distance to be the infimumMore generally, for any two nonempty subsets defineNote that so we can simply write where Similarly,
For example,
The squared Euclidean distance is a measure of how "close" two sets are. In particular, if two sets are compact, then their squared Euclidean distance is zero if and only if they are equal. Thus, we may quantify how close to convexity Q is by upper-bounding
For any bounded subset define its circumradius to be the infimum of the radius of all balls containing it (as shown in the diagram). More formally, Now we can state
Shapley–Folkman theorem —
where we use the notation to mean "the sum of the D largest terms".
Note that this upper bound depends on the dimension of ambient space and the shapes of the summands, but not on the number of summands.
Shapley–Folkman–Starr theorem
Define the inner radius of a bounded subset to be the infimum of such that, for any , there exists a ball of radius such that .

For example, let be two nested balls, then the circumradius of is the radius of , but its inner radius is the radius of .
Since for any bounded subset , the following theorem is a refinement:
Shapley–Folkman–Starr theorem — .
In particular, if we have an infinite sequence of nonempty, bounded subsets of , and if there exists some such that the inner radius of each is upper-bounded by , then This can be interpreted as stating that, as long as we have an upper bound on the inner radii, performing "Minkowski-averaging" would get us closer and closer to a convex set.
Other proofs of the results
There have been many proofs of these results, from the original, to the later Arrow and Hahn, Cassels, Schneider, etc. An abstract and elegant proof by Ekeland has been extended by Artstein. Different proofs have also appeared in unpublished papers. An elementary proof of the Shapley–Folkman lemma can be found in the book by Bertsekas, together with applications in estimating the duality gap in separable optimization problems and zero-sum games.
Usual proofs of these results are nonconstructive: they establish only the existence of the representation, but do not provide an algorithm for computing the representation. In 1981, Starr published an iterative algorithm for a less sharp version of the Shapley–Folkman–Starr theorem.
A proof of the results
The following proof of Shapley–Folkman lemma is from. The proof idea is to lift the representation of from to , use Carathéodory's theorem for conic hulls, then drop back to .
Proof of Shapley–Folkman lemmaFor each , represent as , where is a large finite number, , and .
Now "lift" the representation from to . Define where is the vector in that has 1 at coordinate , and 0 at all other coordinates.
With this, we have a lifted representation
That is, is in the conic hull of .
By Carathéodory's theorem for conic hulls, we have an alternative representation
such that , and at most of them are nonzero. Since we defined
this alternative representation is also a representation for .
We argue that for any , there must be at least one value of for which is nonzero. Remember that we defined , the entry of , to be . At the same time, from the lifted representation of , We drop all terms on the r.h.s. for which since they are zero. The remaining terms take the form , so we find the equation It follows that there is at least one element of the sum on the r.h.s. that is non-zero.
Combining the fact that for each value of there is a non-zero , together with the fact that there are at most of that are nonzero, we conclude that there can only be at most elements of for which there are at least two of that are nonzero.
Thus we obtain a representation
where for at most of , the term is not in .
The following "probabilistic" proof of Shapley–Folkman–Starr theorem is from.
We can interpret in probabilistic terms: , since for some , we can define a random vector , finitely supported in , such that , and .
Then, it is natural to consider the "variance" of a set asWith that, .
Proof: Expand their definitions.
: if then let be finitely supported in such that . Now since is bounded in a ball of radius centered at some , we have .
: use the previous result.
Proof of Shapley–Folkman–Starr theoremIt suffices to show .
, by Shapley–Folkman lemma, there exists a representation , such that partitions .
Now, for each , construct random vectors such that is finitely supported on , with and , where is an arbitrary small number.
Let all such be independent. Then let . Since each is a deterministic vector, we have
Since this is true for arbitrary , we have , and we are done.
History

The lemma of Lloyd Shapley and Jon Folkman was first published by the economist Ross M. Starr, who was investigating the existence of economic equilibria while studying with Kenneth Arrow. In his paper, Starr studied a convexified economy, in which non-convex sets were replaced by their convex hulls; Starr proved that the convexified economy has equilibria that are closely approximated by "quasi-equilibria" of the original economy; moreover, he proved that every quasi-equilibrium has many of the optimal properties of true equilibria, which are proved to exist for convex economies.
Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used to show that central results of (convex) economic theory are good approximations to large economies with non-convexities; for example, quasi-equilibria closely approximate equilibria of a convexified economy. "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Roger Guesnerie.
The topic of non-convex sets in economics has been studied by many Nobel laureates: Shapley himself (2012), Arrow (1972), Robert Aumann (2005), Gérard Debreu (1983), Tjalling Koopmans (1975), Paul Krugman (2008), and Paul Samuelson (1970); the complementary topic of convex sets in economics has been emphasized by these laureates, along with Leonid Hurwicz, Leonid Kantorovich (1975), and Robert Solow (1987).
Applications
The Shapley–Folkman lemma enables researchers to extend results for Minkowski sums of convex sets to sums of general sets, which need not be convex. Such sums of sets arise in economics, in mathematical optimization, and in probability theory; in each of these three mathematical sciences, non-convexity is an important feature of applications.
Economics
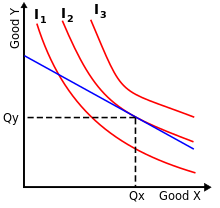
In economics, a consumer's preferences are defined over all "baskets" of goods. Each basket is represented as a non-negative vector, whose coordinates represent the quantities of the goods. On this set of baskets, an indifference curve is defined for each consumer; a consumer's indifference curve contains all the baskets of commodities that the consumer regards as equivalent: That is, for every pair of baskets on the same indifference curve, the consumer does not prefer one basket over another. Through each basket of commodities passes one indifference curve. A consumer's preference set (relative to an indifference curve) is the union of the indifference curve and all the commodity baskets that the consumer prefers over the indifference curve. A consumer's preferences are convex if all such preference sets are convex.
An optimal basket of goods occurs where the budget-line supports a consumer's preference set, as shown in the diagram. This means that an optimal basket is on the highest possible indifference curve given the budget-line, which is defined in terms of a price vector and the consumer's income (endowment vector). Thus, the set of optimal baskets is a function of the prices, and this function is called the consumer's demand. If the preference set is convex, then at every price the consumer's demand is a convex set, for example, a unique optimal basket or a line-segment of baskets.
Non-convex preferences
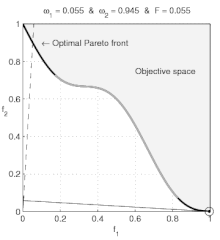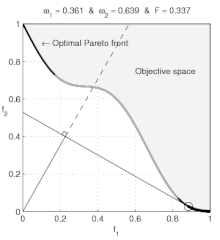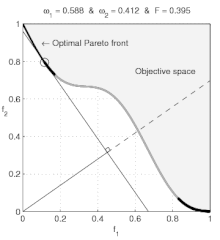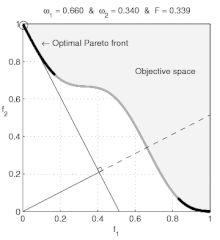
However, if a preference set is non-convex, then some prices determine a budget-line that supports two separate optimal-baskets. For example, we can imagine that, for zoos, a lion costs as much as an eagle, and further that a zoo's budget suffices for one eagle or one lion. We can suppose also that a zoo-keeper views either animal as equally valuable. In this case, the zoo would purchase either one lion or one eagle. Of course, a contemporary zoo-keeper does not want to purchase half of an eagle and half of a lion (or a griffin)! Thus, the zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.
When the consumer's preference set is non-convex, then (for some prices) the consumer's demand is not connected; a disconnected demand implies some discontinuous behavior by the consumer, as discussed by Harold Hotelling:
If indifference curves for purchases be thought of as possessing a wavy character, convex to the origin in some regions and concave in others, we are forced to the conclusion that it is only the portions convex to the origin that can be regarded as possessing any importance, since the others are essentially unobservable. They can be detected only by the discontinuities that may occur in demand with variation in price-ratios, leading to an abrupt jumping of a point of tangency across a chasm when the straight line is rotated. But, while such discontinuities may reveal the existence of chasms, they can never measure their depth. The concave portions of the indifference curves and their many-dimensional generalizations, if they exist, must forever remain in unmeasurable obscurity.
The difficulties of studying non-convex preferences were emphasized by Herman Wold and again by Paul Samuelson, who wrote that non-convexities are "shrouded in eternal darkness ...", according to Diewert.
Nonetheless, non-convex preferences were illuminated from 1959 to 1961 by a sequence of papers in The Journal of Political Economy (JPE). The main contributors were Farrell, Bator, Koopmans, and Rothenberg. In particular, Rothenberg's paper discussed the approximate convexity of sums of non-convex sets. These JPE-papers stimulated a paper by Lloyd Shapley and Martin Shubik, which considered convexified consumer-preferences and introduced the concept of an "approximate equilibrium". The JPE-papers and the Shapley–Shubik paper influenced another notion of "quasi-equilibria", due to Robert Aumann.
Starr's 1969 paper and contemporary economics

Previous publications on non-convexity and economics were collected in an annotated bibliography by Kenneth Arrow. He gave the bibliography to Starr, who was then an undergraduate enrolled in Arrow's (graduate) advanced mathematical-economics course. In his term-paper, Starr studied the general equilibria of an artificial economy in which non-convex preferences were replaced by their convex hulls. In the convexified economy, at each price, the aggregate demand was the sum of convex hulls of the consumers' demands. Starr's ideas interested the mathematicians Lloyd Shapley and Jon Folkman, who proved their eponymous lemma and theorem in "private correspondence", which was reported by Starr's published paper of 1969.
In his 1969 publication, Starr applied the Shapley–Folkman–Starr theorem. Starr proved that the "convexified" economy has general equilibria that can be closely approximated by "quasi-equilibria" of the original economy, when the number of agents exceeds the dimension of the goods: Concretely, Starr proved that there exists at least one quasi-equilibrium of prices popt with the following properties:
- For each quasi-equilibrium's prices popt, all consumers can choose optimal baskets (maximally preferred and meeting their budget constraints).
- At quasi-equilibrium prices popt in the convexified economy, every good's market is in equilibrium: Its supply equals its demand.
- For each quasi-equilibrium, the prices "nearly clear" the markets for the original economy: an upper bound on the distance between the set of equilibria of the "convexified" economy and the set of quasi-equilibria of the original economy followed from Starr's corollary to the Shapley–Folkman theorem.
Starr established that
"in the aggregate, the discrepancy between an allocation in the fictitious economy generated by and some allocation in the real economy is bounded in a way that is independent of the number of economic agents. Therefore, the average agent experiences a deviation from intended actions that vanishes in significance as the number of agents goes to infinity".
Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used in economic theory. Roger Guesnerie summarized their economic implications: "Some key results obtained under the convexity assumption remain (approximately) relevant in circumstances where convexity fails. For example, in economies with a large consumption side, preference nonconvexities do not destroy the standard results". "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Guesnerie. The topic of non-convex sets in economics has been studied by many Nobel laureates: Arrow (1972), Robert Aumann (2005), Gérard Debreu (1983), Tjalling Koopmans (1975), Paul Krugman (2008), and Paul Samuelson (1970); the complementary topic of convex sets in economics has been emphasized by these laureates, along with Leonid Hurwicz, Leonid Kantorovich (1975), and Robert Solow (1987). The Shapley–Folkman–Starr results have been featured in the economics literature: in microeconomics, in general-equilibrium theory, in public economics (including market failures), as well as in game theory, in mathematical economics, and in applied mathematics (for economists). The Shapley–Folkman–Starr results have also influenced economics research using measure and integration theory.
Mathematical optimization

The Shapley–Folkman lemma has been used to explain why large minimization problems with non-convexities can be nearly solved (with iterative methods whose convergence proofs are stated for only convex problems). The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.
Preliminaries of optimization theory
Nonlinear optimization relies on the following definitions for functions:
- Graph(f) = { (x, f(x) ) }
- The epigraph of a real-valued function f is the set of points above the graph
- Epi(f) = { (x, u) : f(x) ≤ u }.
- A real-valued function is defined to be a convex function if its epigraph is a convex set.
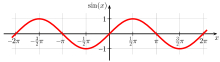
For example, the quadratic function f(x) = x is convex, as is the absolute value function g(x) = |x|. However, the sine function (pictured) is non-convex on the interval (0, π).
Additive optimization problems
In many optimization problems, the objective function f is separable: that is, f is the sum of many summand-functions, each of which has its own argument:
- f(x) = f( (x1, ..., x ) ) = Σ fn(xn).
For example, problems of linear optimization are separable. Given a separable problem with an optimal solution, we fix an optimal solution
- xmin = (x1, ..., x )min
with the minimum value f(xmin). For this separable problem, we also consider an optimal solution (xmin, f(xmin) ) to the "convexified problem", where convex hulls are taken of the graphs of the summand functions. Such an optimal solution is the limit of a sequence of points in the convexified problem
- (xj, f(xj) ) ∈ Σ Conv (Graph( fn ) ).
Of course, the given optimal-point is a sum of points in the graphs of the original summands and of a small number of convexified summands, by the Shapley–Folkman lemma.
This analysis was published by Ivar Ekeland in 1974 to explain the apparent convexity of separable problems with many summands, despite the non-convexity of the summand problems. In 1973, the young mathematician Claude Lemaréchal was surprised by his success with convex minimization methods on problems that were known to be non-convex; for minimizing nonlinear problems, a solution of the dual problem need not provide useful information for solving the primal problem, unless the primal problem be convex and satisfy a constraint qualification. Lemaréchal's problem was additively separable, and each summand function was non-convex; nonetheless, a solution to the dual problem provided a close approximation to the primal problem's optimal value. Ekeland's analysis explained the success of methods of convex minimization on large and separable problems, despite the non-convexities of the summand functions. Ekeland and later authors argued that additive separability produced an approximately convex aggregate problem, even though the summand functions were non-convex. The crucial step in these publications is the use of the Shapley–Folkman lemma. The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.
Probability and measure theory
Convex sets are often studied with probability theory. Each point in the convex hull of a (non-empty) subset Q of a finite-dimensional space is the expected value of a simple random vector that takes its values in Q, as a consequence of Carathéodory's lemma. Thus, for a non-empty set Q, the collection of the expected values of the simple, Q-valued random vectors equals Q's convex hull; this equality implies that the Shapley–Folkman–Starr results are useful in probability theory. In the other direction, probability theory provides tools to examine convex sets generally and the Shapley–Folkman–Starr results specifically. The Shapley–Folkman–Starr results have been widely used in the probabilistic theory of random sets, for example, to prove a law of large numbers, a central limit theorem, and a large-deviations principle. These proofs of probabilistic limit theorems used the Shapley–Folkman–Starr results to avoid the assumption that all the random sets be convex.
A probability measure is a finite measure, and the Shapley–Folkman lemma has applications in non-probabilistic measure theory, such as the theories of volume and of vector measures. The Shapley–Folkman lemma enables a refinement of the Brunn–Minkowski inequality, which bounds the volume of sums in terms of the volumes of their summand-sets. The volume of a set is defined in terms of the Lebesgue measure, which is defined on subsets of Euclidean space. In advanced measure-theory, the Shapley–Folkman lemma has been used to prove Lyapunov's theorem, which states that the range of a vector measure is convex. Here, the traditional term "range" (alternatively, "image") is the set of values produced by the function. A vector measure is a vector-valued generalization of a measure; for example, if p1 and p2 are probability measures defined on the same measurable space, then the product function p1 p2 is a vector measure, where p1 p2 is defined for every event ω by
- (p1 p2)(ω)=(p1(ω), p2(ω)).
Lyapunov's theorem has been used in economics, in ("bang-bang") control theory, and in statistical theory. Lyapunov's theorem has been called a continuous counterpart of the Shapley–Folkman lemma, which has itself been called a discrete analogue of Lyapunov's theorem.
Notes
- "Eternal darkness" describes the Hell of John Milton's Paradise Lost, whose concavity is compared to the Serbonian Bog in Book II, lines 592–594:
Milton's description of concavity serves as the literary epigraph prefacing chapter seven of Arrow & Hahn (1980, p. 169), "Markets with non-convex preferences and production", which presents the results of Starr (1969).A gulf profound as that Serbonian Bog
Betwixt Damiata and Mount Casius old,
Where Armies whole have sunk. - The limit of a sequence is a member of the closure of the original set, which is the smallest closed set that contains the original set. The Minkowski sum of two closed sets need not be closed, so the following inclusion can be strict
- Clos(P) + Clos(Q) ⊆ Clos( Clos(P) + Clos(Q) );
- Aubin & Ekeland (1976) and Ekeland (1999, pp. 362–364) also considered the convex closure of a problem of non-convex minimization—that is, the problem defined as the closed convex hull of the epigraph of the original problem. Their study of duality gaps was extended by Di Guglielmo to the quasiconvex closure of a non-convex minimization problem—that is, the problem defined as the closed convex hull of the lower level sets.
- ^ Starr (1969)
- ^ Howe (1979, p. 1)
- ^ Starr (2008)
- ^ Ekeland (1999, pp. 357–359): Published in the first English edition of 1976, Ekeland's appendix proves the Shapley–Folkman lemma, also acknowledging Lemaréchal's experiments on page 373.
- ^ Bertsekas (1996, pp. 364–381) acknowledging Ekeland (1999) on page 374 and Aubin & Ekeland (1976) on page 381:
Bertsekas (1996, pp. 364–381) describes an application of Lagrangian dual methods to the scheduling of electrical power plants ("unit commitment problems"), where non-convexity appears because of integer constraints:
- ^ Artstein & Vitale (1975, pp. 881–882)
- ^ Carter (2001, p. 94)
- Arrow & Hahn (1980, p. 375)
- ^ Rockafellar (1997, p. 10)
- Arrow & Hahn (1980, p. 376), Rockafellar (1997, pp. 10–11), and Green & Heller (1981, p. 37)
- Arrow & Hahn (1980, p. 385) and Rockafellar (1997, pp. 11–12)
- Schneider (1993, p. xi) and Rockafellar (1997, p. 16)
- Rockafellar (1997, p. 17) and Starr (1997, p. 78)
- Schneider (1993, pp. 2–3)
- Arrow & Hahn (1980, p. 387)
- Starr (1969, pp. 35–36)
- Schneider (1993, p. 140) credits this result to Borwein & O'Brien (1978)
- Starr (1969, p. 36)
- Schneider (1993, p. 129)
- ^ Starr (1969, p. 37)
- Schneider (1993, pp. 129–130)
- Arrow & Hahn (1980, pp. 392–395)
- ^ Cassels (1975, pp. 435–436)
- Schneider (1993, p. 128)
- Ekeland (1999, pp. 357–359)
- Artstein (1980, p. 180)
- Anderson, Robert M. (14 March 2005). "1 The Shapley–Folkman theorem" (PDF). Economics 201B: Nonconvex preferences and approximate equilibria. Berkeley, Calif.: Economics Department, University of California, Berkeley. pp. 1–5. Retrieved 1 January 2011.
- Bertsekas, Dimitri P. (2009). Convex Optimization Theory. Belmont, Mass.: Athena Scientific. ISBN 978-1-886529-31-1.
- Starr, Ross M. (1981). "Approximation of points of convex hull of a sum of sets by points of the sum: An elementary approach". Journal of Economic Theory. 25 (2): 314–317. doi:10.1016/0022-0531(81)90010-7. MR 0640201.
- Zhou, Lin (June 1993). "A simple proof of the Shapley-Folkman theorem". Economic Theory. 3 (2): 371–372. doi:10.1007/bf01212924. ISSN 0938-2259.
- ^ Guesnerie (1989, p. 138)
- Mas-Colell (1985, pp. 58–61) and Arrow & Hahn (1980, pp. 76–79)
- Arrow & Hahn (1980, pp. 79–81)
- Starr (1969, p. 26): "After all, one may be indifferent between an automobile and a boat, but in most cases one can neither drive nor sail the combination of half boat, half car."
- Hotelling (1935, p. 74)
- Wold (1943b, pp. 231 and 239–240) and Wold & Juréen (1953, p. 146)
- Samuelson (1950, pp. 359–360):
It will be noted that any point where the indifference curves are convex rather than concave cannot be observed in a competitive market. Such points are shrouded in eternal darkness—unless we make our consumer a monopsonist and let him choose between goods lying on a very convex "budget curve" (along which he is affecting the price of what he buys). In this monopsony case, we could still deduce the slope of the man's indifference curve from the slope of the observed constraint at the equilibrium point.
- Diewert (1982, pp. 552–553)
- Farrell (1959, 1961a, 1961b)
- Bator (1961a, 1961b)
- Koopmans (1961, p. 478) and others—for example, Farrell (1959, pp. 390–391) and Farrell (1961a, p. 484), Bator (1961a, pp. 482–483), Rothenberg (1960, p. 438), and Starr (1969, p. 26)—commented on Koopmans (1957, pp. 1–126, especially 9–16 , 23–35 , and 35–37 )
- Rothenberg (1960, p. 447, 1961)
- Arrow & Hahn (1980, p. 182)
- Shapley & Shubik (1966, p. 806)
- ^ Aumann (1966, pp. 1–2) uses results from Aumann (1964, 1965)
- Taking the convex hull of non-convex preferences had been discussed earlier by Wold (1943b, p. 243) and by Wold & Juréen (1953, p. 146), according to Diewert (1982, p. 552).
- ^ Starr & Stinchcombe (1999, pp. 217–218)
- Arrow & Hahn (1980, pp. 169–182) and Starr (1969, pp. 27–33)
- Green & Heller (1981, p. 44)
- Guesnerie (1989, pp. 99)
- Mas-Colell (1987)
- Varian (1992, pp. 393–394)
Mas-Colell, Whinston & Green (1995, pp. 627–630)
- Arrow & Hahn (1980, pp. 169–182)
Mas-Colell (1985, pp. 52–55, 145–146, 152–153, and 274–275)
Hildenbrand (1974, pp. 37, 115–116, 122, and 168)
Starr (1997, p. 169)
Ellickson (1994, pp. xviii, 306–310, 312, 328–329, 347, and 352)
- Laffont, Jean-Jacques (1988). "3. Nonconvexities". Fundamentals of public economics. MIT Press. pp. 63–65. ISBN 0-262-12127-1.
- Salanié (2000, pp. 112–113 and 107–115)
- Ichiishi (1983, pp. 24–25)
- Cassels (1981, pp. 127 and 33–34)
- ^ Aubin (2007, pp. 458–476)
- Carter (2001, pp. 93–94, 143, 318–319, 375–377, and 416)
- Trockel (1984, p. 30)
- ^ Bertsekas (1999, p. 496)
- Rockafellar (1997, p. 23)
- Lemaréchal (1973, p. 38)
Lemaréchal's experiments were discussed in later publications:
Aardal (1995, pp. 2–3)
Hiriart-Urruty & Lemaréchal (1993, pp. 143–145, 151, 153, and 156)
- ^ Ekeland, Ivar (1974). "Une estimation a priori en programmation non convexe". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. Séries A et B (in French). 279: 149–151. ISSN 0151-0509. MR 0395844.
- Aubin & Ekeland (1976, pp. 226, 233, 235, 238, and 241)
- Di Guglielmo (1977, pp. 287–288)
- Schneider & Weil (2008, p. 45)
- Cassels (1975, pp. 433–434)
- Molchanov (2005, pp. 195–198, 218, 232, 237–238 and 407)
- ^ Puri & Ralescu (1985, pp. 154–155)
- Weil (1982, pp. 203, and 205–206)
- Cerf (1999, pp. 243–244) uses applications of the Shapley–Folkman lemma from Puri & Ralescu (1985, pp. 154–155).
- Ruzsa (1997, p. 345)
- Tardella (1990, pp. 478–479)
- Vind (1964, pp. 168 and 175) was noted by the winner of the 1983 Nobel Prize in Economics, Gérard Debreu. Debreu (1991, p. 4) wrote:
The concept of a convex set (i.e., a set containing the segment connecting any two of its points) had repeatedly been placed at the center of economic theory before 1964. It appeared in a new light with the introduction of integration theory in the study of economic competition: If one associates with every agent of an economy an arbitrary set in the commodity space and if one averages those individual sets over a collection of insignificant agents, then the resulting set is necessarily convex. But explanations of the ... functions of prices ... can be made to rest on the convexity of sets derived by that averaging process. Convexity in the commodity space obtained by aggregation over a collection of insignificant agents is an insight that economic theory owes ... to integration theory.
- Artstein (1980, pp. 172–183)
- Mas-Colell (1978, p. 210)
References
- Aardal, Karen (March 1995). "Optima interview - Claude Lemaréchal" (PDF). Optima: Mathematical Programming Society Newsletter. 45: 2–4. Retrieved 2 February 2011.
- Arrow, Kenneth J.; Hahn, Frank H. (1980) . General competitive analysis. Advanced Textbooks in Economics. Vol. 12 (reprint of San Francisco, CA: Holden-Day, Inc. Mathematical Economics Texts 6 ed.). Amsterdam: North-Holland. ISBN 0-444-85497-5. MR 0439057.
- Artstein, Zvi (1980). "Discrete and continuous bang-bang and facial spaces, or: Look for the extreme points". SIAM Review. 22 (2): 172–185. doi:10.1137/1022026. JSTOR 2029960. MR 0564562. Republished in a festschrift for Robert J. Aumann, winner of the 2008 Nobel Prize in Economics:
- Artstein, Zvi (1995). "22 Discrete and continuous bang–bang and facial spaces or: Look for the extreme points". In Hart, Sergiu; Neyman, Abraham (eds.). Game and economic theory: Selected contributions in honor of Robert J. Aumann. Ann Arbor, Mich.: University of Michigan Press. pp. 449–462. ISBN 0-472-10673-2. Archived from the original on 24 May 2011.
- Artstein, Zvi; Vitale, Richard A. (1975). "A strong law of large numbers for random compact sets". The Annals of Probability. 3 (5): 879–882. doi:10.1214/aop/1176996275. JSTOR 2959130. MR 0385966. Zbl 0313.60012. PE euclid.ss/1176996275.
- Aubin, Jean-Pierre (2007). "14.2 Duality in the case of non-convex integral criterion and constraints (especially 14.2.3 The Shapley–Folkman theorem, pages 463–465)". Mathematical methods of game and economic theory (Reprint with new preface of 1982 North-Holland revised English ed.). Mineola, NY: Dover Publications. ISBN 978-0-486-46265-3. MR 2449499.
- Aubin, J. P.; Ekeland, I. (1976). "Estimates of the duality gap in nonconvex optimization". Mathematics of Operations Research. 1 (3): 225–245. doi:10.1287/moor.1.3.225. JSTOR 3689565. MR 0449695.
- Aumann, Robert J. (January–April 1964). "Markets with a continuum of traders". Econometrica. 32 (1–2): 39–50. doi:10.2307/1913732. JSTOR 1913732. MR 0172689.
- Aumann, Robert J. (August 1965). "Integrals of set-valued functions". Journal of Mathematical Analysis and Applications. 12 (1): 1–12. doi:10.1016/0022-247X(65)90049-1. MR 0185073.
- Aumann, Robert J. (January 1966). "Existence of competitive equilibrium in markets with a continuum of traders". Econometrica. 34 (1): 1–17. doi:10.2307/1909854. JSTOR 1909854. MR 0191623.
- Bator, Francis M. (October 1961a). "On convexity, efficiency, and markets". The Journal of Political Economy. 69 (5): 480–483. doi:10.1086/258540. JSTOR 1828537.
- Bator, Francis M. (October 1961b). "On convexity, efficiency, and markets: Rejoinder". Journal of Political Economy. 69 (5): 489. doi:10.1086/258542. JSTOR 1828539.
- Bertsekas, Dimitri P. (1999). "5.1.6 Separable problems and their geometry". Nonlinear Programming (Second ed.). Cambridge, Mass.: Athena Scientific. pp. 494–498. ISBN 1-886529-00-0.
- Bertsekas, Dimitri P. (1996). "5.6 Large scale separable integer programming problems and the exponential method of multipliers". Constrained optimization and Lagrange multiplier methods. Belmont, Mass.: Athena Scientific. ISBN 1-886529-04-3. MR 0690767. Reprint of (1982) Academic Press.
- Bertsekas, Dimitri P.; Lauer, Gregory S.; Sandell, Nils R. Jr.; Posbergh, Thomas A. (January 1983). "Optimal short-term scheduling of large-scale power systems" (PDF). IEEE Transactions on Automatic Control. 28 (1): 1–11. doi:10.1109/tac.1983.1103136. Retrieved 2 February 2011. Proceedings of 1981 IEEE Conference on Decision and Control, San Diego, CA, December 1981, pp. 432–443.
- Borwein, J. M.; O'Brien, R. C. (1978). "Cancellation characterizes convexity". Nanta Mathematica (Nanyang University). 11: 100–102. ISSN 0077-2739. MR 0510842.
- Carter, Michael (2001). Foundations of mathematical economics. Cambridge, Mass.: MIT Press. ISBN 0-262-53192-5. MR 1865841. (Author's website with answers to exercises). Archived from the original on 15 September 2006.
- Cassels, J. W. S. (1975). "Measures of the non-convexity of sets and the Shapley–Folkman–Starr theorem". Mathematical Proceedings of the Cambridge Philosophical Society. 78 (3): 433–436. doi:10.1017/S0305004100051884. MR 0385711.
- Cassels, J. W. S. (1981). "Appendix A Convex sets". Economics for mathematicians. London Mathematical Society lecture note series. Vol. 62. Cambridge, UK: Cambridge University Press. ISBN 0-521-28614-X. MR 0657578.
- Cerf, Raphaël (1999). "Large deviations for sums of i.i.d. random compact sets". Proceedings of the American Mathematical Society. 127 (8): 2431–2436. doi:10.1090/S0002-9939-99-04788-7. MR 1487361.
- Debreu, Gérard (March 1991). "The Mathematization of economic theory". The American Economic Review. 81 (Presidential address delivered at the 103rd meeting of the American Economic Association, 29 December 1990, Washington, DC): 1–7. JSTOR 2006785.
- Di Guglielmo, F. (1977). "Nonconvex duality in multiobjective optimization". Mathematics of Operations Research. 2 (3): 285–291. doi:10.1287/moor.2.3.285. JSTOR 3689518. MR 0484418.
- Diewert, W. E. (1982). "12 Duality approaches to microeconomic theory". In Arrow, Kenneth Joseph; Intriligator, Michael D. (eds.). Handbook of mathematical economics. Handbooks in Economics. Vol. 2. Amsterdam: North-Holland Publishing. pp. 535–599. doi:10.1016/S1573-4382(82)02007-4. ISBN 978-0-444-86127-6. MR 0648778.
- Ekeland, Ivar (1999) . "Appendix I: An a priori estimate in convex programming". In Ekeland, Ivar; Temam, Roger (eds.). Convex analysis and variational problems. Classics in Applied Mathematics. Vol. 28 (Corrected reprinting of the North-Holland ed.). Philadelphia: Society for Industrial and Applied Mathematics (SIAM). pp. 357–373. ISBN 0-89871-450-8. MR 1727362.
- Ellickson, Bryan (1994). Competitive equilibrium: Theory and applications. Cambridge University Press. doi:10.1017/CBO9780511609411. ISBN 978-0-521-31988-1.
- Farrell, M. J. (August 1959). "The Convexity assumption in the theory of competitive markets". The Journal of Political Economy. 67 (4): 371–391. doi:10.1086/258197. JSTOR 1825163.
- Farrell, M. J. (October 1961a). "On Convexity, efficiency, and markets: A Reply". Journal of Political Economy. 69 (5): 484–489. doi:10.1086/258541. JSTOR 1828538.
- Farrell, M. J. (October 1961b). "The Convexity assumption in the theory of competitive markets: Rejoinder". Journal of Political Economy. 69 (5): 493. doi:10.1086/258544. JSTOR 1828541.
- Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". In Arrow, Kenneth Joseph; Intriligator, Michael D. (eds.). Handbook of mathematical economics. Handbooks in Economics. Vol. 1. Amsterdam: North-Holland Publishing. pp. 15–52. doi:10.1016/S1573-4382(81)01005-9. ISBN 0-444-86126-2. MR 0634800.
- Guesnerie, Roger (1989). "First-best allocation of resources with nonconvexities in production". In Cornet, Bernard; Tulkens, Henry (eds.). Contributions to Operations Research and Economics: The twentieth anniversary of CORE (Papers from the symposium held in Louvain-la-Neuve, January 1987). Cambridge, Mass.: MIT Press. pp. 99–143. ISBN 0-262-03149-3. MR 1104662.
- Hildenbrand, Werner (1974). Core and equilibria of a large economy. Princeton studies in mathematical economics. Vol. 5. Princeton, NJ: Princeton University Press. ISBN 978-0-691-04189-6. MR 0389160.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "XII Abstract duality for practitioners". Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften . Vol. 306. Berlin: Springer-Verlag. pp. 136–193 (and bibliographical comments on pp. 334–335). ISBN 3-540-56852-2. MR 1295240.
- Hotelling, Harold (January 1935). "Demand functions with limited budgets". Econometrica. 3 (1): 66–78. doi:10.2307/1907346. JSTOR 1907346.
- Howe, Roger (November 1979). On the tendency toward convexity of the vector sum of sets (PDF) (Report). Cowles Foundation discussion papers. Vol. 538. New Haven, Conn.: Cowles Foundation for Research in Economics, Yale University. Retrieved 15 January 2011.
- Ichiishi, Tatsuro (1983). Game theory for economic analysis. Economic theory, econometrics, and mathematical economics. New York: Academic Press . ISBN 0-12-370180-5. MR 0700688.
- Koopmans, Tjalling C. (1957). "Allocation of resources and the price system". In Koopmans, Tjalling C (ed.). Three essays on the state of economic science. New York: McGraw–Hill Book Company. pp. 1–126. ISBN 0-07-035337-9.
- Koopmans, Tjalling C. (October 1961). "Convexity assumptions, allocative efficiency, and competitive equilibrium". The Journal of Political Economy. 69 (5): 478–479. doi:10.1086/258539. JSTOR 1828536.
- Lemaréchal, Claude (April 1973). Utilisation de la dualité dans les problémes non convexes (Report) (in French). Domaine de Voluceau, Rocquencourt, Le Chesnay, France: IRIA (now INRIA), Laboratoire de recherche en informatique et automatique.
- Mas-Colell, Andreu (1978). "A note on the core equivalence theorem: How many blocking coalitions are there?". Journal of Mathematical Economics. 5 (3): 207–215. doi:10.1016/0304-4068(78)90010-1. MR 0514468.
- Mas-Colell, Andreu (1985). "1.L Averages of sets". The Theory of general economic equilibrium: A differentiable approach. Econometric Society monographs. Vol. 9. Cambridge University Press. ISBN 0-521-26514-2. MR 1113262.
- Mas-Colell, A. (1987). "Non-convexity". In Eatwell, John; Milgate, Murray; Newman, Peter (eds.). The new Palgrave: A dictionary of economics (first ed.). Palgrave Macmillan. pp. 653–661. doi:10.1057/9780230226203.3173. ISBN 9780333786765. (PDF file at Mas-Colell's homepage).
- Mas-Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (1995). "17.1 Large economies and nonconvexities". Microeconomic theory. Oxford University Press. ISBN 978-0-19-507340-9.
- Molchanov, Ilya (2005). "3 Minkowski addition". Theory of random sets. Probability and its applications. London: Springer-Verlag London. pp. 194–240. doi:10.1007/1-84628-150-4. ISBN 978-1-84996-949-9. MR 2132405.
- Puri, Madan L.; Ralescu, Dan A. (1985). "Limit theorems for random compact sets in Banach space". Mathematical Proceedings of the Cambridge Philosophical Society. 97 (1): 151–158. Bibcode:1985MPCPS..97..151P. doi:10.1017/S0305004100062691. MR 0764504.
- Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton Landmarks in Mathematics. Princeton, NJ: Princeton University Press. ISBN 0-691-01586-4. MR 1451876.. Reprint of the 1970 (MR274683) Princeton Mathematical Series 28
- Rothenberg, Jerome (October 1960). "Non-convexity, aggregation, and Pareto optimality". The Journal of Political Economy. 68 (5): 435–468. doi:10.1086/258363. JSTOR 1830308.
- Rothenberg, Jerome (October 1961). "Comments on non-convexity". Journal of Political Economy. 69 (5): 490–492. doi:10.1086/258543. JSTOR 1828540.
- Ruzsa, Imre Z. (1997). "The Brunn–Minkowski inequality and nonconvex sets". Geometriae Dedicata. 67 (3): 337–348. doi:10.1023/A:1004958110076. MR 1475877.
- Salanié, Bernard (2000). "7 Nonconvexities". Microeconomics of market failures. Cambridge, Mass.: MIT Press. pp. 107–125. ISBN 0-262-19443-0. English translation of the (1998) French Microéconomie: Les défaillances du marché (Economica, Paris)
- Samuelson, Paul A. (November 1950). "The problem of integrability in utility theory". Economica. New Series. 17 (68): 355–385. doi:10.2307/2549499. JSTOR 2549499. MR 0043436.
- Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of Mathematics and its Applications. Vol. 44. Cambridge, UK: Cambridge University Press. ISBN 0-521-35220-7. MR 1216521.
- Schneider, Rolf; Weil, Wolfgang (2008). Stochastic and integral geometry. Probability and its applications. Springer. doi:10.1007/978-3-540-78859-1. ISBN 978-3-540-78858-4. MR 2455326.
- Shapley, L. S.; Shubik, M. (October 1966). "Quasi-cores in a monetary economy with nonconvex preferences". Econometrica. 34 (4): 805–827. doi:10.2307/1910101. JSTOR 1910101. Zbl 0154.45303. Archived from the original on 24 September 2017.
- Starr, Ross M. (1969). "Quasi-equilibria in markets with non-convex preferences (Appendix 2: The Shapley–Folkman theorem, pp. 35–37)". Econometrica. 37 (1): 25–38. doi:10.2307/1909201. JSTOR 1909201.
- Starr, Ross M. (2008). "Shapley–Folkman theorem". In Durlauf, Steven N.; Blume, Lawrence E. (eds.). The new Palgrave dictionary of economics (Second ed.). Palgrave Macmillan. pp. 317–318 (1st ed.). doi:10.1057/9780230226203.1518. ISBN 978-0-333-78676-5.
- Starr, Ross M. (1997). "8 Convex sets, separation theorems, and non-convex sets in R (new chapters 22 and 25–26 in (2011) second ed.)". General equilibrium theory: An introduction (1st ed.). Cambridge, UK: Cambridge University Press. ISBN 0-521-56473-5. MR 1462618.
- Starr, R. M.; Stinchcombe, M. B. (1999). "Exchange in a network of trading posts". In Chichilnisky, Graciela (ed.). Markets, information and uncertainty: Essays in economic theory in honor of Kenneth J. Arrow. Cambridge, UK: Cambridge University Press. pp. 217–234. doi:10.1017/CBO9780511896583. ISBN 978-0-521-08288-4.
- Tardella, Fabio (1990). "A new proof of the Lyapunov convexity theorem". SIAM Journal on Control and Optimization. 28 (2): 478–481. doi:10.1137/0328026. MR 1040471.
- Trockel, Walter (1984). Market demand: An analysis of large economies with nonconvex preferences. Lecture Notes in Economics and Mathematical Systems. Vol. 223. Berlin: Springer-Verlag. ISBN 3-540-12881-6. MR 0737006.
- Varian, Hal R. (1992). "21.2 Convexity and size". Microeconomic Analysis (3rd ed.). W. W. Norton & Company. ISBN 978-0-393-95735-8. MR 1036734.
- Vind, Karl (May 1964). "Edgeworth-allocations in an exchange economy with many traders". International Economic Review. 5 (2): 165–177. doi:10.2307/2525560. JSTOR 2525560.
- Weil, Wolfgang (1982). "An application of the central limit theorem for Banach-space–valued random variables to the theory of random sets". Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete [Probability Theory and Related Fields]. 60 (2): 203–208. doi:10.1007/BF00531823. MR 0663901.
- Wold, Herman (1943b). "A synthesis of pure demand analysis II". Skandinavisk Aktuarietidskrift [Scandinavian Actuarial Journal]. 26: 220–263. doi:10.1080/03461238.1943.10404737. MR 0011939.
- Wold, Herman; Juréen, Lars (in association with Wold) (1953). "8 Some further applications of preference fields (pp. 129–148)". Demand analysis: A study in econometrics. Wiley publications in statistics. New York: John Wiley and Sons. MR 0064385.
External links
- Anderson, Robert M. (March 2005). "1 The Shapley–Folkman theorem" (PDF). Economics 201B: Nonconvex preferences and approximate equilibria. Berkeley, Calif.: Economics Department, University of California, Berkeley. pp. 1–5. Retrieved 15 January 2011.
- Starr, Ross M. (September 2009). "8 Convex sets, separation theorems, and non-convex sets in R (Section 8.2.3 Measuring non-convexity, the Shapley–Folkman theorem)" (PDF). General equilibrium theory: An introduction. pp. 3–6. doi:10.1017/CBO9781139174749. ISBN 9781139174749. MR 1462618. (Draft of second edition, from Starr's course at the Economics Department of the University of California, San Diego). Archived from the original (PDF) on 1 July 2010. Retrieved 15 January 2011.
- Starr, Ross M. (May 2007). "Shapley–Folkman theorem" (PDF). pp. 1–3. (Draft of article for the second edition of New Palgrave Dictionary of Economics). Retrieved 15 January 2011.
| Geometry | |
|---|---|
| Euclidean geometry | |
| Non-Euclidean geometry | |
| Other | |
| Lists | |
| Convex analysis and variational analysis | |
|---|---|
| Basic concepts | |
| Topics (list) | |
| Maps | |
| Main results (list) | |
| Sets | |
| Series | |
| Duality | |
| Applications and related | |
Categories:
 is a convex set but the
is a convex set but the  is not, because the line segment joining two distinct points
is not, because the line segment joining two distinct points  is not a subset of the circle.
is not a subset of the circle.
 The subset of the integers {0,1,2} is contained in the
The subset of the integers {0,1,2} is contained in the 




 and
and  is the square
is the square  .
. By the principle of induction it is easy to see that
By the principle of induction it is easy to see that



 is the Minkowski sum of the summands.
is the Minkowski sum of the summands.
 , for any x ∈ Conv(Q), there exist elements qn ∈ Conv(Qn) such that
, for any x ∈ Conv(Q), there exist elements qn ∈ Conv(Qn) such that  . The Shapley–Folkman lemma refines this statement.
. The Shapley–Folkman lemma refines this statement.


 and any point
and any point  define their squared Euclidean distance to be the
define their squared Euclidean distance to be the  More generally, for any two nonempty subsets
More generally, for any two nonempty subsets  define
define Note that
Note that  so we can simply write
so we can simply write  where
where  Similarly,
Similarly, 


 define its circumradius
define its circumradius  to be the infimum of the radius of all
to be the infimum of the radius of all  Now we can state
Now we can state

 to mean "the sum of the D largest terms".
to mean "the sum of the D largest terms".
 of a bounded subset
of a bounded subset  to be the infimum of
to be the infimum of  such that, for any
such that, for any  , there exists a ball
, there exists a ball  of radius
of radius  .
. be two nested balls, then the circumradius of
be two nested balls, then the circumradius of  is the radius of
is the radius of  .
.
 for any bounded subset
for any bounded subset  .
.
 of nonempty, bounded subsets of
of nonempty, bounded subsets of  , and if there exists some
, and if there exists some  such that the inner radius of each
such that the inner radius of each  is upper-bounded by
is upper-bounded by  , then
, then  This can be interpreted as stating that, as long as we have an upper bound on the inner radii, performing "Minkowski-averaging" would get us closer and closer to a convex set.
This can be interpreted as stating that, as long as we have an upper bound on the inner radii, performing "Minkowski-averaging" would get us closer and closer to a convex set.
 from
from  , use
, use  , represent
, represent  as
as  , where
, where  is a large finite number,
is a large finite number,  , and
, and  .
.
 from
from  where
where  is the vector in
is the vector in  that has 1 at coordinate
that has 1 at coordinate  That is,
That is,  is in the conic hull of
is in the conic hull of  .
.
 such that
such that  , and at most
, and at most  of them are nonzero. Since we defined
of them are nonzero. Since we defined
 , there must be at least one value of
, there must be at least one value of  for which
for which  is nonzero. Remember that we defined
is nonzero. Remember that we defined  , the
, the  entry of
entry of  . At the same time, from the lifted representation of
. At the same time, from the lifted representation of 
 We drop all terms on the r.h.s. for which
We drop all terms on the r.h.s. for which  since they are zero. The remaining terms take the form
since they are zero. The remaining terms take the form  , so we find the equation
, so we find the equation
 It follows that there is at least one element of the sum on the r.h.s. that is non-zero.
It follows that there is at least one element of the sum on the r.h.s. that is non-zero.
 , together with the fact that there are at most
, together with the fact that there are at most  elements of
elements of  for which there are at least two of
for which there are at least two of  where for at most
where for at most  is not in
is not in  in probabilistic terms:
in probabilistic terms:  , since
, since  for some
for some  , we can define a random vector
, we can define a random vector  , finitely supported in
, finitely supported in  , such that
, such that  , and
, and  .
.
 With that,
With that,  .
. : Expand their definitions.
: Expand their definitions.
 : if
: if  . Now since
. Now since  centered at some
centered at some  , we have
, we have  .
.
 : use the previous result.
: use the previous result.
 .
.
 , by Shapley–Folkman lemma, there exists a representation
, by Shapley–Folkman lemma, there exists a representation  , such that
, such that  partitions
partitions  .
.
 , construct random vectors
, construct random vectors  such that
such that  and
and  , where
, where  is an arbitrary small number.
is an arbitrary small number.
 . Since each
. Since each  is a deterministic vector, we have
is a deterministic vector, we have

 , and we are done.
, and we are done.
 ) ) = Σ fn(xn).
) ) = Σ fn(xn).