Misplaced Pages

Squigonometry or p-trigonometry is a branch of mathematics that extends traditional trigonometry to shapes other than circles, particularly to squircles, in the p-norm. Unlike trigonometry, which deals with the relationships between angles and side lengths of triangles and uses trigonometric functions, squigonometry focuses on analogous relationships within the context of a unit squircle.

Squigonometric functions are mostly used to solve certain indefinite integrals, using a method akin to trigonometric substitution.: This approach allows for the integration of functions that are otherwise computationally difficult to handle.

Squigonometry has been applied to find expressions for the volume of superellipsoids, such as the superegg.

Etymology

The term squigonometry is a portmanteau of squircle and trigonometry. The first use of the term "squigonometry" is undocumented: the coining of the word possibly emerged from mathematical curiosity and the need to solve problems involving squircle geometries. As mathematicians sought to generalize trigonometric ideas beyond circular shapes, they naturally extended these concepts to squircles, leading to the creation of new functions.

Nonetheless, it is well established that the idea of parametrizing curves that aren't perfect circles has been around for around 300 years. Over the span of three centuries, many mathematicians have thought about using functions similar to trigonometric functions to parameterize these generalized curves.

Squigonometric functions

Cosquine and squine

Definition through unit squircle

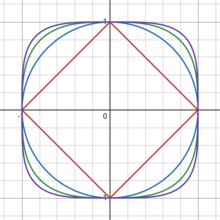
The cosquine and squine functions, denoted as ${\displaystyle cq_{p}(t)}$ and ${\displaystyle sq_{p}(t),}$ can be defined analogously to trigonometric functions on a unit circle, but instead using the coordinates of points on a unit squircle, described by the equation:

${\displaystyle |x|^{p}+|y|^{p}=1}$

where ${\displaystyle p}$ is a real number greater than or equal to 1. Here ${\displaystyle x}$ corresponds to ${\displaystyle cq_{p}(t)}$ and ${\displaystyle y}$ corresponds to ${\displaystyle sq_{p}(t)}$

Notably, when ${\displaystyle p=2}$, the squigonometric functions coincide with the trigonometric functions.

Definition through differential equations

Similarly to how trigonometric functions are defined through differential equations, the cosquine and squine functions are also uniquely determined by solving the coupled initial value problem

${\displaystyle {\begin{cases}x'(t)=-|y(t)|^{p-1}\\y'(t)=|x(t)|^{p-1}\\x(0)=1\\y(0)=0\end{cases}}}$

Where ${\displaystyle x}$ corresponds to ${\displaystyle cq_{p}(t)}$ and ${\displaystyle y}$ corresponds to ${\displaystyle sq_{p}(t)}$.

Definition through analysis

The definition of sine and cosine through integrals can be extended to define the squigonometric functions. Let ${\displaystyle 1<p<\infty }$ and define a differentiable function ${\displaystyle F_{p}:\rightarrow {\mathbb {R} }}$ by:

${\displaystyle F_{p}(x)=\int _{0}^{x}{\frac {1}{{(1-t^{p})}^{\tfrac {p-1}{p}}}}\,dt}$

Since ${\displaystyle F_{p}}$ is strictly increasing it is a one-to-one function on ${\displaystyle }$ with range ${\displaystyle }$, where ${\displaystyle \pi _{p}}$ is defined as follows:

${\displaystyle \pi _{p}=2\int _{0}^{1}{\frac {1}{{(1-t^{p})}^{\tfrac {p-1}{p}}}}\,dt}$

Let ${\displaystyle sq_{p}}$ be the inverse of ${\displaystyle F_{p}}$ on ${\displaystyle }$. This function can be extended to ${\displaystyle }$ by defining the following relationship:

${\displaystyle sq_{p}(x)=sq_{p}(\pi _{p}-x)}$

By this means ${\displaystyle sq_{p}}$ is differentiable in ${\displaystyle {\mathbb {R} }}$ and, corresponding to this, the function ${\displaystyle cq_{p}}$ is defined by:

${\displaystyle cq_{p}(x)={\frac {d}{dx}}sq_{p}(x)}$

Tanquent, cotanquent, sequent and cosequent

The tanquent, cotanquent, sequent and cosequent functions can be defined as follows:

${\displaystyle tq_{p}(t)={\frac {sq_{p}(t)}{cq_{p}(t)}}}$

${\displaystyle ctq_{p}(t)={\frac {cq_{p}(t)}{sq_{p}(t)}}}$

${\displaystyle seq_{p}(t)={\frac {1}{cq_{p}(t)}}}$

${\displaystyle cseq_{p}(t)={\frac {1}{sq_{p}(t)}}}$

Inverse squigonometric functions

General versions of the inverse squine and cosquine can be derived from the initial value problem above. Let ${\displaystyle x=cq_{p}(y)}$; by the inverse function rule, ${\displaystyle {\frac {dx}{dy}}=-^{p-1}=(1-x^{p})^{(p-1)/p}}$. Solving for ${\displaystyle y}$ gives the definition of the inverse cosquine:

${\displaystyle y=cq_{p}^{-1}(x)=\int _{x}^{1}({\frac {1}{1-t^{p}}})^{\frac {p-1}{p}}\,dt}$

Similarly, the inverse squine is defined as:

${\displaystyle sq_{p}^{-1}(x)=\int _{0}^{x}({\frac {1}{1-t^{p}}})^{\frac {p-1}{p}}\,dt}$

Multiple ways to approach Squigonometry

Other parameterizations of squircles give rise to alternate definitions of these functions. For example, Edmunds, Lang, and Gurka define ${\displaystyle {\tilde {F}}_{p}(x)}$ as:

${\displaystyle {\tilde {F}}_{p}(x)=\int _{0}^{x}(1-t^{p})^{-(1/p)}\,dt}$.

Since ${\displaystyle F_{p}}$ is strictly increasing it has a =n inverse which, by analogy with the case ${\displaystyle p=2}$, we denote by ${\displaystyle \sin _{p}}$. This is defined on the interval ${\displaystyle }$, where ${\displaystyle {\tilde {\pi }}_{p}}$ is defined as follows:

${\displaystyle {\tilde {\pi }}_{p}=2\int _{0}^{1}(1-t^{p})^{-(1/p)}\,dt}$.

Because of this, we know that ${\displaystyle \sin _{p}}$ is strictly increasing on ${\displaystyle }$, ${\displaystyle \sin _{p}(0)=0}$ and ${\displaystyle \sin _{p}({\tilde {\pi }}_{p}/2)=1}$. We extend ${\displaystyle \sin _{p}}$ to ${\displaystyle }$ by defining:

${\displaystyle \sin _{p}(x)=\sin _{p}({\tilde {\pi }}_{p}-x)}$ for ${\displaystyle x\in }$ Similarly ${\displaystyle \cos _{p}(x)=(1-(\sin _{p}(x))^{p})^{\frac {1}{p}}}$.

Thus ${\displaystyle \cos _{p}}$ is strictly decreasing on ${\displaystyle }$, ${\displaystyle \cos _{p}(0)=1}$ and ${\displaystyle \cos _{p}({\tilde {\pi }}_{2}/2)=0}$. Also:

${\displaystyle |\sin _{p}x|^{p}+|\cos _{p}x|^{p}=1}$ .

This is immediate if ${\displaystyle x\in }$, but it holds for all ${\displaystyle x\in \mathbb {R} }$ in view of symmetry and periodicity.

Applications

Solving integrals

Squigonometric substitution can be used to solve integrals, such as integrals in the generic form ${\displaystyle I=\int _{a}^{b}({1-t^{p}})^{\frac {1}{p}}\,dt}$.

See also

• Astroid
• Ellipsoid
• L spaces
• Oval
• Squround

References

1. ^ Poodiack, Robert D. (April 2016). "Squigonometry, Hyperellipses, and Supereggs". Mathematics Magazine. 89 (2).
2. Poodiack, Robert D.; Wood, William E. (2022). Squigonometry: The Study of Imperfect Circles (1st ed.). Springer Nature Switzerland. p. 1.
3. Elbert, Á. (1987-09-01). "On the half-linear second order differential equations". Acta Mathematica Hungarica. 49 (3): 487–508. doi:10.1007/BF01951012. ISSN 1588-2632.
4. Wood, William E. (October 2011). "Squigonometry". Mathematics Magazine. 84 (4): 264.
5. Chebolu, Sunil; Hatfield, Andrew; Klette, Riley; Moore, Cristopher; Warden, Elizabeth (Fall 2022). "Trigonometric functions in the p-norm". BSU Undergraduate Mathematics Exchange. 16 (1): 4, 5.
6. Girg, Petr E.; Kotrla, Lukáš (February 2014). Differentiability properties of p-trigonometric functions. p. 104.
7. Edmunds, David E.; Gurka, Petr; Lang, Jan (2012). "Properties of generalized trigonometric functions". Journal of Approximation Theory. 164 (1): 49.
8. Edmunds, David (2011). Eigenvalues, Embeddings and Generalised Trigonometric Functions. Springer-Verlag Berlin Heidelberg.

• Trigonometry