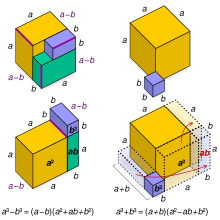
In mathematics, the sum of two cubes is a cubed number added to another cubed number.
Factorization
Every sum of cubes may be factored according to the identity in elementary algebra.
Binomial numbers generalize this factorization to higher odd powers.
"SOAP" method
The mnemonic "SOAP", standing for "Same, Opposite, Always Positive", is sometimes used to memorize the correct placement of the addition and subtraction symbols while factorizing cubes. When applying this method to the factorization, "Same" represents the first term with the same sign as the original expression, "Opposite" represents the second term with the opposite sign as the original expression, and "Always Positive" represents the third term and is always positive.
original
signSame Opposite Always
Positivea + b = (a + b)(a − ab + b) a − b = (a − b)(a + ab + b)
Proof
Starting with the expression, and multiplying by a + b distributing a and b over , and canceling the like terms,
Similarly for the difference of cubes,
Fermat's last theorem
Fermat's last theorem in the case of exponent 3 states that the sum of two non-zero integer cubes does not result in a non-zero integer cube. The first recorded proof of the exponent 3 case was given by Euler.
Taxicab and Cabtaxi numbers
A Taxicab number is the smallest positive number that can be expressed as a sum of two positive integer cubes in n distinct ways. The smallest taxicab number after Ta(1) = 1, is Ta(2) = 1729, expressed as
- or
Ta(3), the smallest taxicab number expressed in 3 different ways, is 87,539,319, expressed as
- , or
A Cabtaxi number is the smallest positive number that can be expressed as a sum of two integer cubes in n ways, allowing the cubes to be negative or zero as well as positive. The smallest cabtaxi number after Cabtaxi(1) = 0, is Cabtaxi(2) = 91, expressed as:
- or
Cabtaxi(3), the smallest Cabtaxi number expressed in 3 different ways, is 4104, expressed as
- , or
See also
- Difference of two squares
- Binomial number
- Sophie Germain's identity
- Aurifeuillean factorization
- Fermat's last theorem
References
- ^ McKeague, Charles P. (1986). Elementary Algebra (3rd ed.). Academic Press. p. 388. ISBN 0-12-484795-1.
- Kropko, Jonathan (2016). Mathematics for social scientists. Los Angeles, LA: Sage. p. 30. ISBN 9781506304212.
- Dickson, L. E. (1917). "Fermat's Last Theorem and the Origin and Nature of the Theory of Algebraic Numbers". Annals of Mathematics. 18 (4): 161–187. doi:10.2307/2007234. ISSN 0003-486X. JSTOR 2007234.
- "A001235 - OEIS". oeis.org. Retrieved 2023-01-04.
- Schumer, Peter (2008). "Sum of Two Cubes in Two Different Ways". Math Horizons. 16 (2): 8–9. doi:10.1080/10724117.2008.11974795. JSTOR 25678781.
- Silverman, Joseph H. (1993). "Taxicabs and Sums of Two Cubes". The American Mathematical Monthly. 100 (4): 331–340. doi:10.2307/2324954. ISSN 0002-9890. JSTOR 2324954.
Further reading
- Broughan, Kevin A. (January 2003). "Characterizing the Sum of Two Cubes" (PDF). Journal of Integer Sequences. 6 (4): 46. Bibcode:2003JIntS...6...46B.
 in
in  and multiplying by a + b
and multiplying by a + b
 distributing a and b over
distributing a and b over  and canceling the like terms,
and canceling the like terms,


 or
or 
 ,
,  or
or 
 or
or 
 ,
,  or
or 