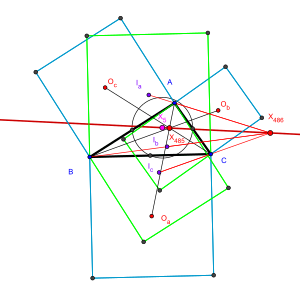
In Euclidean geometry, the Vecten points are two triangle centers, points associated with any triangle. They may be found by constructing three squares on the sides of the triangle, connecting each square centre by a line to the opposite triangle point, and finding the point where these three lines meet. The outer and inner Vecten points differ according to whether the squares are extended outward from the triangle sides, or inward.
The Vecten points are named after an early 19th-century French mathematician named Vecten, who taught mathematics with Gergonne in Nîmes and published a study of the figure of three squares on the sides of a triangle in 1817.
Outer Vecten point
Let △ABC be any given plane triangle. On the sides BC, CA, AB of the triangle, construct outwardly drawn three squares with centres Oa, Ob, Oc respectively. Then the lines AOa, BOb, COc are concurrent. The point of concurrence is the outer Vecten point of △ABC.
In Clark Kimberling's Encyclopedia of Triangle Centers, the outer Vecten point is denoted by X(485).
Isogonal conjugate of outer Vecten point is Kenmotu point [ja].
Inner Vecten point
Let △ABC be any given plane triangle. On the sides BC, CA, AB of the triangle, construct inwardly drawn three squares respectively with centres Ia, Ib, Ic respectively. Then the lines AIa, BIb, CIc are concurrent. The point of concurrence is the inner Vecten point of △ABC.
In the Encyclopedia of Triangle Centers, the inner Vecten point is denoted by X(486).
The line X485X486 meets the Euler line at the nine-point center of △ABC. The Vecten points lie on the Kiepert hyperbola.
See also
- Napoleon points, a pair of triangle centers constructed in an analogous way using equilateral triangles instead of squares
References
- Ayme, Jean-Louis, La Figure de Vecten (PDF), retrieved 2014-11-04.
- ^ Kimberling, Clark. "Encyclopedia of Triangle Centers".