
A vortex ring, also called a toroidal vortex, is a torus-shaped vortex in a fluid; that is, a region where the fluid mostly spins around an imaginary axis line that forms a closed loop. The dominant flow in a vortex ring is said to be toroidal, more precisely poloidal.
Vortex rings are plentiful in turbulent flows of liquids and gases, but are rarely noticed unless the motion of the fluid is revealed by suspended particles—as in the smoke rings which are often produced intentionally or accidentally by smokers. Fiery vortex rings are also a commonly produced trick by fire eaters. Visible vortex rings can also be formed by the firing of certain artillery, in mushroom clouds, in microbursts, and rarely in volcanic eruptions.
A vortex ring usually tends to move in a direction that is perpendicular to the plane of the ring and such that the inner edge of the ring moves faster forward than the outer edge. Within a stationary body of fluid, a vortex ring can travel for relatively long distance, carrying the spinning fluid with it.
Structure
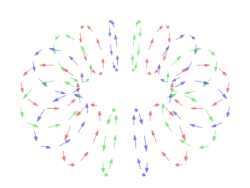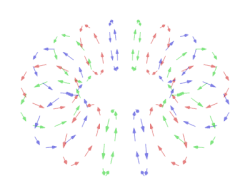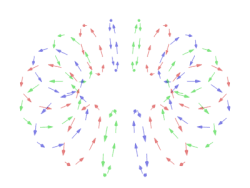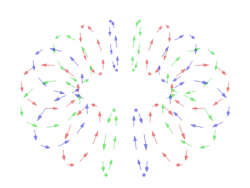
In a typical vortex ring, the fluid particles move in roughly circular paths around an imaginary circle (the core) that is perpendicular to those paths. As in any vortex, the velocity of the fluid is roughly constant except near the core, so that the angular velocity increases towards the core, and most of the vorticity (and hence most of the energy dissipation) is concentrated near it.
Unlike a sea wave, whose motion is only apparent, a moving vortex ring actually carries the spinning fluid along. Just as a rotating wheel lessens friction between a car and the ground, the poloidal flow of the vortex lessens the friction between the core and the surrounding stationary fluid, allowing it to travel a long distance with relatively little loss of mass and kinetic energy, and little change in size or shape. Thus, a vortex ring can carry mass much further and with less dispersion than a jet of fluid. That explains, for instance, why a smoke ring keeps traveling long after any extra smoke blown out with it has stopped and dispersed. These properties of vortex rings are exploited in the vortex ring gun for riot control, and vortex ring toys such as the air vortex cannons.
Formation
Formation process
The formation of vortex rings has fascinated the scientific community for more than a century, starting with William Barton Rogers who made sounding observations of the formation process of air vortex rings in air, air rings in liquids, and liquid rings in liquids. In particular, William Barton Rogers made use of the simple experimental method of letting a drop of liquid fall on a free liquid surface; a falling colored drop of liquid, such as milk or dyed water, will inevitably form a vortex ring at the interface due to the surface tension.
A method proposed by G. I. Taylor to generate a vortex ring is to impulsively start a disk from rest. The flow separates to form a cylindrical vortex sheet and by artificially dissolving the disk, one is left with an isolated vortex ring. This is the case when someone is stirring their cup of coffee with a spoon and observing the propagation of a half-vortex in the cup.
In a laboratory, vortex rings are formed by impulsively discharging fluid through a sharp-edged nozzle or orifice. The impulsive motion of the piston/cylinder system is either triggered by an electric actuator or by a pressurized vessel connected to a control valve. For a nozzle geometry, and at first approximation, the exhaust speed is uniform and equal to the piston speed. This is referred as a parallel starting jet. It is possible to have a conical nozzle in which the streamlines at the exhaust are directed toward the centerline. This is referred as a converging starting jet. The orifice geometry which consists in an orifice plate covering the straight tube exhaust, can be considered as an infinitely converging nozzle but the vortex formation differs considerably from the converging nozzle, principally due to the absence of boundary layer in the thickness of the orifice plate throughout the formation process. The fast moving fluid (A) is therefore discharged into a quiescent fluid (B). The shear imposed at the interface between the two fluids slows down the outer layer of the fluid (A) relatively to the centerline fluid. In order to satisfy the Kutta condition, the flow is forced to detach, curl and roll-up in the form of a vortex sheet. Later, the vortex sheet detaches from the feeding jet and propagates freely downstream due to its self-induced kinematics. This is the process commonly observed when a smoker forms smoke rings from their mouth, and how vortex ring toys work.
Secondary effects are likely to modify the formation process of vortex rings. Firstly, at the very first instants, the velocity profile at the exhaust exhibits extrema near the edge causing a large vorticity flux into the vortex ring. Secondly, as the ring grows in size at the edge of the exhaust, negative vorticity is generated on the outer wall of the generator which considerably reduces the circulation accumulated by the primary ring. Thirdly, as the boundary layer inside the pipe, or nozzle, thickens, the velocity profile approaches the one of a Poiseuille flow and the centerline velocity at the exhaust is measured to be larger than the prescribed piston speed. Last but not least, in the event the piston-generated vortex ring is pushed through the exhaust, it may interact or even merge with the primary vortex, hence modifying its characteristic, such as circulation, and potentially forcing the transition of the vortex ring to turbulence.
Vortex ring structures are easily observable in nature. For instance, a mushroom cloud formed by a nuclear explosion or volcanic eruption, has a vortex ring-like structure. Vortex rings are also seen in many different biological flows; blood is discharged into the left ventricle of the human heart in the form of a vortex ring and jellyfishes or squids were shown to propel themselves in water by periodically discharging vortex rings in the surrounding. Finally, for more industrial applications, the synthetic jet which consists in periodically-formed vortex rings, was proved to be an appealing technology for flow control, heat and mass transfer and thrust generation
Vortex formation number
Prior to Gharib et al. (1998), few studies had focused on the formation of vortex rings generated with long stroke-to-diameter ratios , where is the length of the column of fluid discharged through the exhaust and is the diameter of the exhaust. For short stroke ratios, only one isolated vortex ring is generated and no fluid is left behind in the formation process. For long stroke ratios, however, the vortex ring is followed by some energetic fluid, referred as the trailing jet. On top of showing experimental evidence of the phenomenon, an explanation of the phenomenon was provided in terms of energy maximisation invoking a variational principle first reported by Kelvin and later proven by Benjamin (1976), or Friedman & Turkington (1981). Ultimately, Gharib et al. (1998) observed the transition between these two states to occur at a non-dimensional time , or equivalently a stroke ratio , of about 4. The robustness of this number with respect to initial and boundary conditions suggested the quantity to be a universal constant and was thus named formation number.
The phenomenon of 'pinch-off', or detachment, from the feeding starting jet is observed in a wide range of flows observed in nature. For instance, it was shown that biological systems such as the human heart or swimming and flying animals generate vortex rings with a stroke-to-diameter ratio close to the formation number of about 4, hence giving ground to the existence of an optimal vortex ring formation process in terms of propulsion, thrust generation and mass transport. In particular, the squid lolliguncula brevis was shown to propel itself by periodically emitting vortex rings at a stroke-ratio close to 4. Moreover, in another study by Gharib et al (2006), the formation number was used as an indicator to monitor the health of the human heart and identify patients with dilated cardiomyopathy.
Other examples
Vortex ring state in helicopters
Main article: Vortex ring state
Air vortices can form around the main rotor of a helicopter, causing a dangerous condition known as vortex ring state (VRS) or "settling with power". In this condition, air that moves down through the rotor turns outward, then up, inward, and then down through the rotor again. This re-circulation of flow can negate much of the lifting force and cause a catastrophic loss of altitude. Applying more power (increasing collective pitch) serves to further accelerate the downwash through which the main-rotor is descending, exacerbating the condition.
In the human heart
A vortex ring is formed in the left ventricle of the human heart during cardiac relaxation (diastole), as a jet of blood enters through the mitral valve. This phenomenon was initially observed in vitro and subsequently strengthened by analyses based on color Doppler mapping and magnetic resonance imaging. Some recent studies have also confirmed the presence of a vortex ring during rapid filling phase of diastole and implied that the process of vortex ring formation can influence mitral annulus dynamics.
Bubble rings
Releasing air underwater forms bubble rings, which are vortex rings of water with bubbles (or even a single donut-shaped bubble) trapped along its axis line. Such rings are often produced by scuba divers and dolphins.
Volcanoes

| This list is incomplete; you can help by adding missing items. (May 2012) |
Under particular conditions, some volcanic vents can produce large visible vortex rings. Though a rare phenomenon, several volcanoes have been observed emitting massive vortex rings as erupting steam and gas condense, forming visible toroidal clouds:
- Mount Etna, Italy (Sicily)
- Stromboli, Italy (Aeolian Islands)
- Eyjafjallajökull, Iceland
- Hekla, Iceland
- Tungurahua, Ecuador
- Pacaya, Guatemala
- Mount Redoubt, United States (Alaska)
- Mount Aso, Japan (Kyushu)
- Whakaari (White Island), New Zealand
- Gunung Slamet, Indonesia (Central Java)
- Momotombo, Nicaragua (León)
Separated vortex rings

There has been research and experiments on the existence of separated vortex rings (SVR) such as those formed in the wake of the pappus of a dandelion. This special type of vortex ring effectively stabilizes the seed as it travels through the air and increases the lift generated by the seed. Compared to a standard vortex ring, which is propelled downstream, the axially symmetric SVR remains attached to the pappus for the duration of its flight and uses drag to enhance the travel. These dandelion seed structures have been used to create tiny battery-free wireless sensors that can float in the wind and be dispersed across a large area.
Theory
Historical studies
The formation of vortex rings has fascinated the scientific community for more than a century, starting with William Barton Rogers who made sounding observations of the formation process of air vortex rings in air, air rings in liquids, and liquid rings in liquids. In particular, William Barton Rogers made use of the simple experimental method of letting a drop of liquid fall on a free liquid surface; a falling colored drop of liquid, such as milk or dyed water, will inevitably form a vortex ring at the interface due to the surface tension.
Vortex rings were first mathematically analyzed by the German physicist Hermann von Helmholtz, in his 1858 paper On Integrals of the Hydrodynamical Equations which Express Vortex-motion.
Circular vortex lines
For a single zero-thickness vortex ring, the vorticity is represented by a Dirac delta function as where denotes the coordinates of the vortex filament of strength in a constant half-plane. The Stokes stream function is: with where and are respectively the least and the greatest distance from the point to the vortex line, and where is the complete elliptic integral of the first kind and is the complete elliptic integral of the second kind.
A circular vortex line is the limiting case of a thin vortex ring. Because there is no core thickness, the speed of the ring is infinite, as well as the kinetic energy. The hydrodynamic impulse can be expressed in term of the strength, or 'circulation' , of the vortex ring as .
Thin-core vortex rings
The discontinuity introduced by the Dirac delta function prevents the computation of the speed and the kinetic energy of a circular vortex line. It is however possible to estimate these quantities for a vortex ring having a finite small thickness. For a thin vortex ring, the core can be approximated by a disk of radius which is assumed to be infinitesimal compared to the radius of the ring , i.e. . As a consequence, inside and in the vicinity of the core ring, one may write: , and , and, in the limit of , the elliptic integrals can be approximated by and .
For a uniform vorticity distribution in the disk, the Stokes stream function can therefore be approximated by </ref>
The resulting circulation , hydrodynamic impulse and kinetic energy are
It is also possible to find the translational ring speed (which is finite) of such isolated thin-core vortex ring: which finally results in the well-known expression found by Kelvin and published in the English translation by Tait of von Helmholtz's paper:
Spherical vortices
Main article: Hill's spherical vortexHill's spherical vortex is an example of steady vortex flow and may be used to model vortex rings having a vorticity distribution extending to the centerline. More precisely, the model supposes a linearly distributed vorticity distribution in the radial direction starting from the centerline and bounded by a sphere of radius as: where is the constant translational speed of the vortex.
Finally, the Stokes stream function of Hill's spherical vortex can be computed and is given by: The above expressions correspond to the stream function describing a steady flow. In a fixed frame of reference, the stream function of the bulk flow having a speed should be added.
The circulation, the hydrodynamic impulse and the kinetic energy can also be calculated in terms of the translational speed and radius : </ref>
Such a structure or an electromagnetic equivalent has been suggested as an explanation for the internal structure of ball lightning. For example, Shafranov used a magnetohydrodynamic (MHD) analogy to Hill's stationary fluid mechanical vortex to consider the equilibrium conditions of axially symmetric MHD configurations, reducing the problem to the theory of stationary flow of an incompressible fluid. In axial symmetry, he considered general equilibrium for distributed currents and concluded under the Virial Theorem that if there were no gravitation, a bounded equilibrium configuration could exist only in the presence of an azimuthal current.
Fraenkel-Norbury model
The Fraenkel-Norbury model of isolated vortex ring, sometimes referred as the standard model, refers to the class of steady vortex rings having a linear distribution of vorticity in the core and parametrised by the mean core radius , where is the area of the vortex core and is the radius of the ring. Approximate solutions were found for thin-core rings, i.e. , and thick Hill's-like vortex rings, i.e. , Hill's spherical vortex having a mean core radius of precisely . For mean core radii in between, one must rely on numerical methods. Norbury (1973) found numerically the resulting steady vortex ring of given mean core radius, and this for a set of 14 mean core radii ranging from 0.1 to 1.35. The resulting streamlines defining the core of the ring were tabulated, as well as the translational speed. In addition, the circulation, the hydrodynamic impulse and the kinetic energy of such steady vortex rings were computed and presented in non-dimensional form.
Instabilities
A kind of azimuthal radiant-symmetric structure was observed by Maxworthy when the vortex ring traveled around a critical velocity, which is between the turbulence and laminar states. Later Huang and Chan reported that if the initial state of the vortex ring is not perfectly circular, another kind of instability would occur. An elliptical vortex ring undergoes an oscillation in which it is first stretched in the vertical direction and squeezed in the horizontal direction, then passes through an intermediate state where it is circular, then is deformed in the opposite way (stretched in the horizontal direction and squeezed in the vertical) before reversing the process and returning to the original state.
See also
- Air vortex cannon
- Bubble ring – underwater vortex ring
- Mushroom cloud
- Toroidal moment
- Vortex ring gun
- Vortex ring toy
References
- "The Microburst as a Vortex Ring". Forecast Research Branch. NASA. Archived from the original on 2011-07-18. Retrieved 2010-01-10.
- Chambers, Joseph R. (Jan 1, 2003). "Wind Shear". Concept to Reality: Contributions of the Langley Research Center to US Civil Aircraft of the 1990s (PDF). NASA. pp. 185–198. hdl:2060/20030059513. Archived from the original on 2007-10-09. Retrieved 2007-10-09.
- ^ "Vortex rings made of water vapour rise from Italy's Mount Etna volcano". ABC News. 8 April 2024. Retrieved 8 April 2024.
- Batchelor, G.K. (1967), An introduction to fluid dynamics, Cambridge University Press, ISBN 978-0-521-09817-5
- Physics in a Toroidal Vortex: Air Cannon Physics Central, American Physical Society . Accessed January 2011.
- Rogers, W. B. (1858). "On the formation of rotating rings by air and liquids under certain conditions of discharge". Am. J. Sci. Arts. 26: 246–258. Retrieved 2021-08-09.
- Taylor, G. I. (1953). "Formation of a vortex ring by giving an impulse to a circular disk and then dissolving it away". J. Appl. Phys. 24 (1): 104. Bibcode:1953JAP....24..104T. doi:10.1063/1.1721114. Retrieved 2021-08-09.
- ^ Didden, N. (1979). "On the formation of vortex rings: rolling-up and production of circulation". J. Appl. Math. Phys. (ZAMP). 30 (1): 101–116. Bibcode:1979ZaMP...30..101D. doi:10.1007/BF01597484. S2CID 120056371. Retrieved 2021-08-09.
- ^ Gharib, M.; Rambod, E.; Kheradvar, A.; Sahn, D. J.; Dabiri, J. O. (2006). "Optimal vortex formation as an index of cardiac health". Proceedings of the National Academy of Sciences. 103 (16): 6305–6308. Bibcode:2006PNAS..103.6305G. doi:10.1073/pnas.0600520103. ISSN 0027-8424. PMC 1458873. PMID 16606852.
- Stewart, W. J.; Bartol, I. K.; Krueger, P. S. (2010). "Hydrodynamic fin function of brief squid, Lolliguncula brevis". J. Exp. Biol. 213 (12): 2009–2024. doi:10.1242/jeb.039057. ISSN 0022-0949. PMID 20511514.
- Glezer, A.; Amitay, M. (2002). "Synthetic jets". Annu. Rev. Fluid Mech. 34 (1): 503–529. Bibcode:2002AnRFM..34..503G. doi:10.1146/annurev.fluid.34.090501.094913. Retrieved 2021-08-09.
- ^ Gharib, M.; Rambod, E.; Shariff, K. (1998). "A universal time scale for vortex ring formation". Journal of Fluid Mechanics. 360 (1): 121–140. Bibcode:1998JFM...360..121G. doi:10.1017/s0022112097008410. S2CID 50685764.
- Thomson, W. (1878). "1. Vortex statics". Proceedings of the Royal Society of Edinburgh. 9: 59–73. doi:10.1017/S0370164600031679.
- Benjamin, T. B. (1976). "The alliance of practical and analytical insights into the nonlinear problems of fluid mechanics.". Applications of Methods of Functional Analysis to Problems in Mechanics. Vol. 503. Springer Berlin Heidelberg. pp. 8–29. doi:10.1007/BFb0088744.
- Friedman, A.; Turkington, B. (1981). "Vortex rings: existence and asymptotic estimates" (PDF). Transactions of the American Mathematical Society. 268 (1): 1–37. doi:10.1090/S0002-9947-1981-0628444-6.
- Dabiri, J. O. (2009). "Optimal vortex formation as a unifying principle in biological propulsion". Annual Review of Fluid Mechanics. 41 (1): 17–33. Bibcode:2009AnRFM..41...17D. doi:10.1146/annurev.fluid.010908.165232.
- ^ Dabiri, J. O.; Gharib, M. (2005). "The role of optimal vortex formation in biological fluid transport". Proceedings of the Royal Society B: Biological Sciences. 272 (1572): 1557–1560. doi:10.1098/rspb.2005.3109. PMC 1559837. PMID 16048770.
- Krueger, P. S. (2003). "The significance of vortex ring formation to the impulse and thrust of a starting jet". Physics of Fluids. 15 (5): 1271–1281. Bibcode:2003PhFl...15.1271K. doi:10.1063/1.1564600.
- Stewart, W. J.; Bartol, I. K.; Krueger, P. S. (2010-05-28). "Hydrodynamic fin function of brief squid, Lolliguncula brevis". Journal of Experimental Biology. 213 (12): 2009–2024. doi:10.1242/jeb.039057. ISSN 0022-0949. PMID 20511514.
- Bellhouse, B.J., 1972, Fluid mechanics of a model mitral valve and left ventricle, Cardiovascular Research 6, 199–210.
- Reul, H., Talukder, N., Muller, W., 1981, Fluid mechanics of the natural mitral valve, Journal of Biomechanics 14, 361–372.
- Kim, W.Y., Bisgaard, T., Nielsen, S.L., Poulsen, J.K., Pedersen, E.M., Hasenkam, J.M., Yoganathan, A.P., 1994, Two-dimensional mitral flow velocity profiles in pig models using epicardial echo Doppler Cardiography, J Am Coll Cardiol 24, 532–545.
- Vierendeels, J. A., E. Dick, and P. R. Verdonck, Hydrodynamics of color M-mode Doppler flow wave propagation velocity V(p): A computer study, J. Am. Soc. Echocardiogr. 15:219–224, 2002.
- Kim, W.Y., Walker, P.G., Pedersen, E.M., Poulsen, J.K., Oyre, S., Houlind, K., Yoganathan, A.P., 1995, Left ventricular blood flow patterns in normal subjects: a quantitative analysis by three dimensional magnetic resonance velocity mapping, J Am Coll Cardiol 26, 224–238.
- Kilner, P.J., Yang, G.Z., Wilkes, A.J., Mohiaddin, R.H., Firmin, D.N., Yacoub, M.H., 2000, Asymmetric redirection of flow through the heart, Nature 404, 759–761.
- Kheradvar, A., Milano, M., Gharib, M. Correlation between vortex ring formation and mitral annulus dynamics during ventricular rapid filling, ASAIO Journal, Jan–Feb 2007 53(1): 8–16.
- Kheradvar, A., Gharib, M. Influence of ventricular pressure-drop on mitral annulus dynamics through the process of vortex ring formation, Ann Biomed Eng. 2007 Dec;35(12):2050–64.
- Don White. "Mystery of the Silver Rings". Archived from the original on 2007-10-26. Retrieved 2007-10-25.
- Illustrated Volcano Glossary
- Etna hoops it up BBC News, 2003-03-31.
- Etna 2000 Stromboli Online, 2009-03-12.
- Archived 2012-01-21 at the Wayback Machine Smoke rings of Mount Etna video
- "Smoke rings from Stromboli volcano (June 2006)". www.volcanodiscovery.com.
- Iceland Volcano Blows Spectacular Smoke Ring: Big Pics Discovery News, 2010-05-10.
- "Environment". The Telegraph. Archived from the original on March 26, 2010. Retrieved 2021-01-28.
- Duyck, Bernard. "" Les volcans fument la pipe" - formation de vortex toroidal". Earth of fire. Archived from the original on 2013-07-25. Retrieved 2024-04-08.
- "Pacaya Volcano blows a smoke-ring in farewell Guatemala 2005". May 15, 2011.
- "Mt Redoubt Blowing Smoke Rings". August 30, 2009 – via Flickr.
- "aso volcano smoke ring". February 17, 2012 – via Flickr.
- "DSC_0350.jpg". February 21, 2013 – via Flickr.
- "Cincin Raksasa Muncul di Atas Gunung Slamet - Daerah". touch.metrotvnews.com. Archived from the original on 12 September 2014. Retrieved 17 January 2022.
- "Momotombo - Anillos de humo". YouTube. 2015-12-05. Archived from the original on 2021-12-22. Retrieved 2021-01-28.
- Ledda, P. G.; Siconolfi, L.; Viola, F.; Camarri, S.; Gallaire, F. (2019-07-02). "Flow dynamics of a dandelion pappus: A linear stability approach". Physical Review Fluids. 4 (7): 071901. Bibcode:2019PhRvF...4g1901L. doi:10.1103/physrevfluids.4.071901. hdl:11568/998044. ISSN 2469-990X. S2CID 198429309.
- ^ Cummins, Cathal; Seale, Madeleine; Macente, Alice; Certini, Daniele; Mastropaolo, Enrico; Viola, Ignazio Maria; Nakayama, Naomi (2018). "A separated vortex ring underlies the flight of the dandelion" (PDF). Nature. 562 (7727): 414–418. Bibcode:2018Natur.562..414C. doi:10.1038/s41586-018-0604-2. ISSN 0028-0836. PMID 30333579. S2CID 52988814.
- Yamamoto, Kyoji (November 1971). "Flow of Viscous Fluid at Small Reynolds Numbers Past a Porous Sphere". Journal of the Physical Society of Japan. 31 (5): 1572. Bibcode:1971JPSJ...31.1572Y. doi:10.1143/JPSJ.31.1572.
- Iyer, Vikram; Gaensbauer, Hans; Daniel, Thomas L.; Gollakota, Shyamnath (2022-03-17). "Wind dispersal of battery-free wireless devices". Nature. 603 (7901): 427–433. Bibcode:2022Natur.603..427I. doi:10.1038/s41586-021-04363-9. ISSN 0028-0836. PMID 35296847. S2CID 247499662.
- Rogers, W. B. (1858). "On the formation of rotating rings by air and liquids under certain conditions of discharge". Am. J. Sci. Arts. 26: 246–258.
- ^ Helmholtz, H. (1858). "3. Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen" (PDF). Journal für die reine und angewandte Mathematik. 55: 25–55. doi:10.1515/9783112336489-003. ISBN 9783112336472.
- ^ Helmholtz, H. (1867). "LXIII. On integrals of the hydrodynamical equations, which express vortex-motion". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 33 (226): 485–512. doi:10.1080/14786446708639824.
- Moffatt, K. (2008). "Vortex Dynamics: The Legacy of Helmholtz and Kelvin". In Borisov, A. V.; Kozlov, V. V.; Mamaev, I. S.; Sokolovskiy, M. A. (eds.). IUTAM Symposium on Hamiltonian Dynamics, Vortex Structures, Turbulence. IUTAM Bookseries. Vol. 6. Springer Netherlands. pp. 1–10. doi:10.1007/978-1-4020-6744-0_1. ISBN 978-1-4020-6743-3.
- ^ Lamb, H. (1932). Hydrodynamics. Cambridge University Press. pp. 236–241.
- ^ Hill, M.J.M. (1894). "VI. On a spherical vortex". Philosophical Transactions of the Royal Society of London A. 185: 213–245. Bibcode:1894RSPTA.185..213H. doi:10.1098/rsta.1894.0006.
- Fraenkel, L. E. (1970). "On steady vortex rings of small cross-section in an ideal fluid". Proceedings of the Royal Society A. 316 (1524): 29–62. Bibcode:1970RSPSA.316...29F. doi:10.1098/rspa.1970.0065. S2CID 119895722.
- Fraenkel, L. E. (1972). "Examples of steady vortex rings of small cross-section in an ideal fluid". Journal of Fluid Mechanics. 51 (1): 119–135. Bibcode:1972JFM....51..119F. doi:10.1017/S0022112072001107. S2CID 123465650.
- Norbury, J. (1972). "A steady vortex ring close to Hill's spherical vortex". Mathematical Proceedings of the Cambridge Philosophical Society. 72 (2): 253–284. Bibcode:1972PCPS...72..253N. doi:10.1017/S0305004100047083. S2CID 120436906.
- ^ Norbury, J. (1973). "A family of steady vortex rings". Journal of Fluid Mechanics. 57 (3): 417–431. Bibcode:1973JFM....57..417N. doi:10.1017/S0022112073001266. S2CID 123479437.
- Maxworthy, T. J. (1972) The structure and stability of vortex ring, Fluid Mech. Vol. 51, p. 15
- Huang, J., Chan, K.T. (2007) Dual-Wavelike Instability in Vortex Rings, Proc. 5th IASME/WSEAS Int. Conf. Fluid Mech. & Aerodyn., Greece
External links
- YouTube video of Vortex ring cannon
- Fluid dynamics lecture covering vortices
- An animation of a vortex ring
- Giant vortex ring generator
- Toy Box Physics: Vortices, Air Cannons, and Mushroom Clouds
- Thesis on vortex ring formation and interactions
- Vortex half-ring in a pool, Dianna Cowern (Physics Girl), YouTube
- More experiments with vortex rings in a pool, Dianna Cowern (Physics Girl), YouTube
 , where
, where  is the length of the column of fluid discharged through the exhaust and
is the length of the column of fluid discharged through the exhaust and  is the diameter of the exhaust. For short stroke ratios, only one isolated vortex ring is generated and no fluid is left behind in the formation process. For long stroke ratios, however, the vortex ring is followed by some energetic fluid, referred as the trailing jet. On top of showing experimental evidence of the phenomenon, an explanation of the phenomenon was provided in terms of energy maximisation invoking a variational principle first reported by
is the diameter of the exhaust. For short stroke ratios, only one isolated vortex ring is generated and no fluid is left behind in the formation process. For long stroke ratios, however, the vortex ring is followed by some energetic fluid, referred as the trailing jet. On top of showing experimental evidence of the phenomenon, an explanation of the phenomenon was provided in terms of energy maximisation invoking a variational principle first reported by  , or equivalently a stroke ratio
, or equivalently a stroke ratio  where
where  denotes the coordinates of the vortex filament of strength
denotes the coordinates of the vortex filament of strength  in a constant
in a constant  half-plane. The
half-plane. The  with
with  where
where  and
and  are respectively the least and the greatest distance from the point
are respectively the least and the greatest distance from the point  to the vortex line, and where
to the vortex line, and where  is the
is the  is the
is the  .
.
 which is assumed to be infinitesimal compared to the radius of the ring
which is assumed to be infinitesimal compared to the radius of the ring  , i.e.
, i.e.  . As a consequence, inside and in the vicinity of the core ring, one may write:
. As a consequence, inside and in the vicinity of the core ring, one may write:  ,
,  and
and  , and, in the limit of
, and, in the limit of  , the elliptic integrals can be approximated by
, the elliptic integrals can be approximated by  and
and  .
.
 in the disk, the
in the disk, the 
 , hydrodynamic impulse
, hydrodynamic impulse  and
and 
 which finally results in the well-known expression found by
which finally results in the well-known expression found by 
 where
where  is the constant translational speed of the vortex.
is the constant translational speed of the vortex.
 The above expressions correspond to the stream function describing a steady flow. In a fixed frame of reference, the stream function of the bulk flow having a speed
The above expressions correspond to the stream function describing a steady flow. In a fixed frame of reference, the stream function of the bulk flow having a speed 
 , where
, where  is the area of the vortex core and
is the area of the vortex core and  , and thick Hill's-like vortex rings, i.e.
, and thick Hill's-like vortex rings, i.e.  , Hill's spherical vortex having a mean core radius of precisely
, Hill's spherical vortex having a mean core radius of precisely  . For mean core radii in between, one must rely on numerical methods. Norbury (1973) found numerically the resulting steady vortex ring of given mean core radius, and this for a set of 14 mean core radii ranging from 0.1 to 1.35. The resulting streamlines defining the core of the ring were tabulated, as well as the translational speed. In addition, the circulation, the hydrodynamic impulse and the kinetic energy of such steady vortex rings were computed and presented in non-dimensional form.
. For mean core radii in between, one must rely on numerical methods. Norbury (1973) found numerically the resulting steady vortex ring of given mean core radius, and this for a set of 14 mean core radii ranging from 0.1 to 1.35. The resulting streamlines defining the core of the ring were tabulated, as well as the translational speed. In addition, the circulation, the hydrodynamic impulse and the kinetic energy of such steady vortex rings were computed and presented in non-dimensional form.