| Watkins snark | |
|---|---|
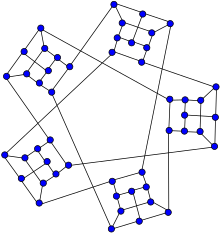 The Watkins snark The Watkins snark | |
| Named after | J. J. Watkins |
| Vertices | 50 |
| Edges | 75 |
| Radius | 7 |
| Diameter | 7 |
| Girth | 5 |
| Automorphisms | 5 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Snark |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Watkins snark is a snark with 50 vertices and 75 edges. It was discovered by John J. Watkins in 1989.
As a snark, the Watkins graph is a connected, bridgeless cubic graph with chromatic index equal to 4. The Watkins snark is also non-planar and non-hamiltonian. It has book thickness 3 and queue number 2.
Another well known snark on 50 vertices is the Szekeres snark, the fifth known snark, discovered by George Szekeres in 1973.
Gallery
-
 The chromatic number of the Watkins snark is 3.
The chromatic number of the Watkins snark is 3.
-
 The chromatic index of the Watkins snark is 4.
The chromatic index of the Watkins snark is 4.
Edges
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ]
References
- Weisstein, Eric W. "Watkins Snark". MathWorld.
- Watkins, J. J. and Wilson, R. J. "A Survey of Snarks." In Graph Theory, Combinatorics, and Applications (Ed. Y. Alavi, G. Chartrand, O. R. Oellermann, and A. J. Schwenk). New York: Wiley, pp. 1129-1144, 1991
- Watkins, J. J. "Snarks." Ann. New York Acad. Sci. 576, 606-622, 1989.
- Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- Szekeres, G. (1973). "Polyhedral decompositions of cubic graphs". Bull. Austral. Math. Soc. 8 (3): 367–387. doi:10.1017/S0004972700042660.
This graph theory-related article is a stub. You can help Misplaced Pages by expanding it. |