Misplaced Pages

Latest revision as of 20:27, 18 December 2024

Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related problems of squaring the circle and trisecting the angle, doubling the cube is now known to be impossible to construct by using only a compass and straightedge, but even in ancient times solutions were known that employed other methods.

According to Eutocius, Archytas was the first to solve the problem of doubling the cube (the so-called Delian problem) with an ingenious geometric construction. The nonexistence of a compass-and-straightedge solution was finally proven by Pierre Wantzel in 1837.

In algebraic terms, doubling a unit cube requires the construction of a line segment of length x, where x = 2; in other words, x = ${\displaystyle {\sqrt{2}}}$, the cube root of two. This is because a cube of side length 1 has a volume of 1 = 1, and a cube of twice that volume (a volume of 2) has a side length of the cube root of 2. The impossibility of doubling the cube is therefore equivalent to the statement that ${\displaystyle {\sqrt{2}}}$ is not a constructible number. This is a consequence of the fact that the coordinates of a new point constructed by a compass and straightedge are roots of polynomials over the field generated by the coordinates of previous points, of no greater degree than a quadratic. This implies that the degree of the field extension generated by a constructible point must be a power of 2. The field extension generated by ${\displaystyle {\sqrt{2}}}$, however, is of degree 3.

Proof of impossibility

We begin with the unit line segment defined by points (0,0) and (1,0) in the plane. We are required to construct a line segment defined by two points separated by a distance of ${\displaystyle {\sqrt{2}}}$. It is easily shown that compass and straightedge constructions would allow such a line segment to be freely moved to touch the origin, parallel with the unit line segment - so equivalently we may consider the task of constructing a line segment from (0,0) to (${\displaystyle {\sqrt{2}}}$, 0), which entails constructing the point (${\displaystyle {\sqrt{2}}}$, 0).

Respectively, the tools of a compass and straightedge allow us to create circles centred on one previously defined point and passing through another, and to create lines passing through two previously defined points. Any newly defined point either arises as the result of the intersection of two such circles, as the intersection of a circle and a line, or as the intersection of two lines. An exercise of elementary analytic geometry shows that in all three cases, both the x- and y-coordinates of the newly defined point satisfy a polynomial of degree no higher than a quadratic, with coefficients that are additions, subtractions, multiplications, and divisions involving the coordinates of the previously defined points (and rational numbers). Restated in more abstract terminology, the new x- and y-coordinates have minimal polynomials of degree at most 2 over the subfield of ${\displaystyle \mathbb {R} }$ generated by the previous coordinates. Therefore, the degree of the field extension corresponding to each new coordinate is 2 or 1.

So, given a coordinate of any constructed point, we may proceed inductively backwards through the x- and y-coordinates of the points in the order that they were defined until we reach the original pair of points (0,0) and (1,0). As every field extension has degree 2 or 1, and as the field extension over ${\displaystyle \mathbb {Q} }$ of the coordinates of the original pair of points is clearly of degree 1, it follows from the tower rule that the degree of the field extension over ${\displaystyle \mathbb {Q} }$ of any coordinate of a constructed point is a power of 2.

Now, p(x) = x − 2 = 0 is easily seen to be irreducible over ${\displaystyle \mathbb {Z} }$ – any factorisation would involve a linear factor (x − k) for some k ∈ ${\displaystyle \mathbb {Z} }$, and so k must be a root of p(x); but also k must divide 2 (by the rational root theorem); that is, k = 1, 2, −1 or −2, and none of these are roots of p(x). By Gauss's Lemma, p(x) is also irreducible over ${\displaystyle \mathbb {Q} }$, and is thus a minimal polynomial over ${\displaystyle \mathbb {Q} }$ for ${\displaystyle {\sqrt{2}}}$. The field extension ${\displaystyle \mathbb {Q} ({\sqrt{2}}):\mathbb {Q} }$ is therefore of degree 3. But this is not a power of 2, so by the above:

• ${\displaystyle {\sqrt{2}}}$ is not the coordinate of a constructible point, so
• a line segment of ${\displaystyle {\sqrt{2}}}$ cannot be constructed with ruler and compass, and
• the cube cannot be doubled using only a ruler and a compass.

History

The problem owes its name to a story concerning the citizens of Delos, who consulted the oracle at Delphi in order to learn how to defeat a plague sent by Apollo. According to Plutarch, however, the citizens of Delos consulted the oracle at Delphi to find a solution for their internal political problems at the time, which had intensified relationships among the citizens. The oracle responded that they must double the size of the altar to Apollo, which was a regular cube. The answer seemed strange to the Delians, and they consulted Plato, who was able to interpret the oracle as the mathematical problem of doubling the volume of a given cube, thus explaining the oracle as the advice of Apollo for the citizens of Delos to occupy themselves with the study of geometry and mathematics in order to calm down their passions.

According to Plutarch, Plato gave the problem to Eudoxus and Archytas and Menaechmus, who solved the problem using mechanical means, earning a rebuke from Plato for not solving the problem using pure geometry. This may be why the problem is referred to in the 350s BC by the author of the pseudo-Platonic Sisyphus (388e) as still unsolved. However another version of the story (attributed to Eratosthenes by Eutocius of Ascalon) says that all three found solutions but they were too abstract to be of practical value.

A significant development in finding a solution to the problem was the discovery by Hippocrates of Chios that it is equivalent to finding two geometric mean proportionals between a line segment and another with twice the length. In modern notation, this means that given segments of lengths a and 2a, the duplication of the cube is equivalent to finding segments of lengths r and s so that

${\displaystyle {\frac {a}{r}}={\frac {r}{s}}={\frac {s}{2a}}.}$

In turn, this means that

${\displaystyle r=a\cdot {\sqrt{2}}.}$

But Pierre Wantzel proved in 1837 that the cube root of 2 is not constructible; that is, it cannot be constructed with straightedge and compass.

Solutions via means other than compass and straightedge

Menaechmus' original solution involves the intersection of two conic curves. Other more complicated methods of doubling the cube involve neusis, the cissoid of Diocles, the conchoid of Nicomedes, or the Philo line. Pandrosion, a probably female mathematician of ancient Greece, found a numerically accurate approximate solution using planes in three dimensions, but was heavily criticized by Pappus of Alexandria for not providing a proper mathematical proof. Archytas solved the problem in the 4th century BC using geometric construction in three dimensions, determining a certain point as the intersection of three surfaces of revolution.

Descartes theory of geometric solution of equations uses a parabola to introduce cubic equations, in this way it is possible to set up an equation whose solution is a cube root of two. Note that the parabola itself is not constructible except by three dimensional methods.

False claims of doubling the cube with compass and straightedge abound in mathematical crank literature (pseudomathematics).

Origami may also be used to construct the cube root of two by folding paper.

Using a marked ruler

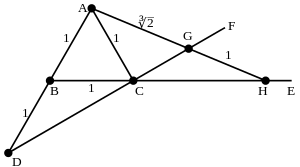
There is a simple neusis construction using a marked ruler for a length which is the cube root of 2 times another length.

1. Mark a ruler with the given length; this will eventually be GH.
2. Construct an equilateral triangle ABC with the given length as side.
3. Extend AB an equal amount again to D.
4. Extend the line BC forming the line CE.
5. Extend the line DC forming the line CF.
6. Place the marked ruler so it goes through A and one end, G, of the marked length falls on ray CF and the other end of the marked length, H, falls on ray CE. Thus GH is the given length.

Then AG is the given length times ${\displaystyle {\sqrt{2}}}$.

In music theory

In music theory, a natural analogue of doubling is the octave (a musical interval caused by doubling the frequency of a tone), and a natural analogue of a cube is dividing the octave into three parts, each the same interval. In this sense, the problem of doubling the cube is solved by the major third in equal temperament. This is a musical interval that is exactly one third of an octave. It multiplies the frequency of a tone by ${\displaystyle 2^{4/12}=2^{1/3}={\sqrt{2}}}$, the side length of the Delian cube.

Explanatory notes

1. The Delian problem shows up in Plato's Republic (c. 380 BC) VII.530

References

1. ^ Kern, Willis F.; Bland, James R. (1934). Solid Mensuration With Proofs. New York: John Wiley & Sons.
2. Menn, Stephen (2015). "How Archytas doubled the cube". In Holmes, Brooke; Fischer, Klaus-Dietrich (eds.). The Frontiers of Ancient Science: Essays in honor of Heinrich von Staden. Beiträge zur Altertumskunde. Vol. 338. De Gruyter. pp. 407–436. doi:10.1515/9783110336337-021.
3. Masià, Ramon (2016). "A new reading of Archytas' doubling of the cube and its implications". Archive for History of Exact Sciences. 70 (2): 175–204. doi:10.1007/s00407-015-0165-9. MR 3458183.
4. Guilbeau, Lucye (1930). "The history of the solution of the cubic equation". Mathematics News Letter. 5 (4): 8–12. doi:10.2307/3027812. JSTOR 3027812.
5. Zhmudʹ, Leonid I︠A︡kovlevich (2006). The Origin of the History of Science in Classical Antiquity. Walter de Gruyter. pp. 84, quoting Plutarch and Theon of Smyrna. ISBN 978-3-11-017966-8.
6. "Plutarch, De E apud Delphos, section 6 386.4". www.perseus.tufts.edu. Retrieved 2024-09-17.
7. Plutarch, De genio Socratis 579.B
8. (Plut., Quaestiones convivales VIII.ii, 718ef)
9. Carl Werner Müller, Die Kurzdialoge der Appendix Platonica, Munich: Wilhelm Fink, 1975, pp. 105–106
10. Knorr, Wilbur Richard (1986), The Ancient Tradition of Geometric Problems, Dover Books on Mathematics, Courier Dover Publications, p. 4, ISBN 9780486675329.
11. T.L. Heath A History of Greek Mathematics, Vol. 1
12. Lützen, Jesper (24 January 2010). "The Algebra of Geometric Impossibility: Descartes and Montucla on the Impossibility of the Duplication of the Cube and the Trisection of the Angle". Centaurus. 52 (1): 4–37. doi:10.1111/j.1600-0498.2009.00160.x.
13. Knorr, Wilbur Richard (1989). "Pappus' texts on cube duplication". Textual Studies in Ancient and Medieval Geometry. Boston: Birkhäuser. pp. 63–76. doi:10.1007/978-1-4612-3690-0_5. ISBN 9780817633875.
14. Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics. Dover. p. 171. ISBN 0486-61348-8.
15. Phillips, R. C. (October 1905), "The equal tempered scale", Musical Opinion and Music Trade Review, 29 (337): 41–42, ProQuest 7191936

External links

• Frédéric Beatrix, Peter Katzlinger: A pretty accurate solution to the Delian problem. In: Parabola Volume 59 (2023) Issue 1, online magazine (ISSN 1446-9723) published by the School of Mathematics and Statistics University of New South Wales
• Doubling the cube, proximity construction as animation (side = 1.259921049894873)—Wikimedia Commons
• "Duplication of the cube", Encyclopedia of Mathematics, EMS Press, 2001
• Doubling the cube. J. J. O'Connor and E. F. Robertson in the MacTutor History of Mathematics archive.
• To Double a Cube – The Solution of Archytas. Excerpt from A History of Greek Mathematics by Sir Thomas Heath.
• Delian Problem Solved. Or Is It? at cut-the-knot.
• Mathologer video: "2000 years unsolved: Why is doubling cubes and squaring circles impossible?"

v t e Algebraic numbers
Algebraic integer Chebyshev nodes Constructible number Conway's constant Cyclotomic field Doubling the cube Eisenstein integer Gaussian integer Golden ratio (φ) Perron number Pisot–Vijayaraghavan number Plastic ratio (ρ) Quadratic irrational number Rational number Root of unity Salem number Silver ratio (σ) Square root of 2 Square root of 3 Square root of 5 Square root of 6 Square root of 7 Supergolden ratio (ψ) Supersilver ratio (ς) Twelfth root of 2
Mathematics portal

v t e Ancient Greek mathematics
Mathematicians (timeline)	Anaxagoras Anthemius Archytas Aristaeus the Elder Aristarchus Aristotle Apollonius Archimedes Autolycus Bion Bryson Callippus Carpus Chrysippus Cleomedes Conon Ctesibius Democritus Dicaearchus Diocles Diophantus Dinostratus Dionysodorus Domninus Eratosthenes Eudemus Euclid Eudoxus Eutocius Geminus Heliodorus Heron Hipparchus Hippasus Hippias Hippocrates Hypatia Hypsicles Isidore of Miletus Leon Marinus Menaechmus Menelaus Metrodorus Nicomachus Nicomedes Nicoteles Oenopides Pappus Perseus Philolaus Philon Philonides Plato Porphyry Posidonius Proclus Ptolemy Pythagoras Serenus Simplicius Sosigenes Sporus Thales Theaetetus Theano Theodorus Theodosius Theon of Alexandria Theon of Smyrna Thymaridas Xenocrates Zeno of Elea Zeno of Sidon Zenodorus
Treatises	Almagest Archimedes Palimpsest Arithmetica Conics (Apollonius) Catoptrics Data (Euclid) Elements (Euclid) Measurement of a Circle On Conoids and Spheroids On the Sizes and Distances (Aristarchus) On Sizes and Distances (Hipparchus) On the Moving Sphere (Autolycus) Optics (Euclid) On Spirals On the Sphere and Cylinder Ostomachion Planisphaerium Spherics (Theodosius) Spherics (Menelaus) The Quadrature of the Parabola The Sand Reckoner
Problems	Constructible numbers Angle trisection Doubling the cube Squaring the circle Problem of Apollonius
Concepts and definitions	Angle Central Inscribed Axiomatic system Axiom Chord Circles of Apollonius Apollonian circles Apollonian gasket Circumscribed circle Commensurability Diophantine equation Doctrine of proportionality Euclidean geometry Golden ratio Greek numerals Incircle and excircles of a triangle Method of exhaustion Parallel postulate Platonic solid Lune of Hippocrates Quadratrix of Hippias Regular polygon Straightedge and compass construction Triangle center
Results	In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon Apollonius Apollonius's theorem Other Aristarchus's inequality Crossbar theorem Heron's formula Irrational numbers Law of sines Menelaus's theorem Pappus's area theorem Problem II.8 of Arithmetica Ptolemy's inequality Ptolemy's table of chords Ptolemy's theorem Spiral of Theodorus
Centers	Cyrene Mouseion of Alexandria Platonic Academy
Related	Ancient Greek astronomy Attic numerals Greek numerals Latin translations of the 12th century Non-Euclidean geometry Philosophy of mathematics Neusis construction History of A History of Greek Mathematics by Thomas Heath algebra timeline arithmetic timeline calculus timeline geometry timeline logic timeline mathematics timeline numbers prehistoric counting numeral systems list Other cultures Arabian/Islamic Babylonian Chinese Egyptian Incan Indian Japanese
Ancient Greece portal • Mathematics portal

• Compass and straightedge constructions
• Cubic irrational numbers
• Euclidean plane geometry
• History of geometry
• Unsolvable puzzles