Misplaced Pages

Pentagonal cupola
Type	Johnson J4 – J5 – J6
Faces	5 triangles 5 squares 1 pentagon 1 decagon
Edges	25
Vertices	15
Vertex configuration	${\displaystyle 10\times (3\times 4\times 10)}$ ${\displaystyle 5\times (3\times 4\times 5\times 4)}$
Symmetry group	${\displaystyle C_{\mathrm {v} }}$
Properties	convex, elementary
Net

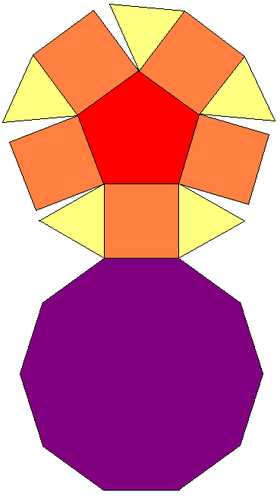In geometry, the pentagonal cupola is one of the Johnson solids (J₅). It can be obtained as a slice of the rhombicosidodecahedron. The pentagonal cupola consists of 5 equilateral triangles, 5 squares, 1 pentagon, and 1 decagon.

Properties

The pentagonal cupola's faces are five equilateral triangles, five squares, one regular pentagon, and one regular decagon. It has the property of convexity and regular polygonal faces, from which it is classified as the fifth Johnson solid. This cupola produces two or more regular polyhedrons by slicing it with a plane, an elementary polyhedron's example.

The following formulae for circumradius ${\displaystyle R}$, and height ${\displaystyle h}$, surface area ${\displaystyle A}$, and volume ${\displaystyle V}$ may be applied if all faces are regular with edge length ${\displaystyle a}$: $${\displaystyle {\begin{aligned}h&={\sqrt {\frac {5-{\sqrt {5}}}{10}}}a&\approx 0.526a,\\R&={\frac {\sqrt {11+4{\sqrt {5}}}}{2}}a&\approx 2.233a,\\A&={\frac {20+5{\sqrt {3}}+{\sqrt {5\left(145+62{\sqrt {5}}\right)}}}{4}}a^{2}&\approx 16.580a^{2},\\V&={\frac {5+4{\sqrt {5}}}{6}}a^{3}&\approx 2.324a^{3}.\end{aligned}}}$$

It has an axis of symmetry passing through the center of both top and base, which is symmetrical by rotating around it at one-, two-, three-, and four-fifth of a full-turn angle. It is also mirror-symmetric relative to any perpendicular plane passing through a bisector of the hexagonal base. Therefore, it has pyramidal symmetry, the cyclic group ${\displaystyle C_{5\mathrm {v} }}$ of order ten.

Related polyhedron

The pentagonal cupola can be applied to construct a polyhedron. A construction that involves the attachment of its base to another polyhedron is known as augmentation; attaching it to prisms or antiprisms is known as elongation or gyroelongation. Some of the Johnson solids with such constructions are: elongated pentagonal cupola ${\displaystyle J_{20}}$, gyroelongated pentagonal cupola ${\displaystyle J_{24}}$, pentagonal orthobicupola ${\displaystyle J_{30}}$, pentagonal gyrobicupola ${\displaystyle J_{31}}$, pentagonal orthocupolarotunda ${\displaystyle J_{32}}$, pentagonal gyrocupolarotunda ${\displaystyle J_{33}}$, elongated pentagonal orthobicupola ${\displaystyle J_{38}}$, elongated pentagonal gyrobicupola ${\displaystyle J_{39}}$, elongated pentagonal orthocupolarotunda ${\displaystyle J_{40}}$, gyroelongated pentagonal bicupola ${\displaystyle J_{46}}$, gyroelongated pentagonal cupolarotunda ${\displaystyle J_{47}}$, augmented truncated dodecahedron ${\displaystyle J_{68}}$, parabiaugmented truncated dodecahedron ${\displaystyle J_{69}}$, metabiaugmented truncated dodecahedron ${\displaystyle J_{70}}$, triaugmented truncated dodecahedron ${\displaystyle J_{71}}$, gyrate rhombicosidodecahedron ${\displaystyle J_{72}}$, parabigyrate rhombicosidodecahedron ${\displaystyle J_{73}}$, metabigyrate rhombicosidodecahedron ${\displaystyle J_{74}}$, and trigyrate rhombicosidodecahedron ${\displaystyle J_{75}}$. Relatedly, a construction from polyhedra by removing one or more pentagonal cupolas is known as diminishment: diminished rhombicosidodecahedron ${\displaystyle J_{76}}$, paragyrate diminished rhombicosidodecahedron ${\displaystyle J_{77}}$, metagyrate diminished rhombicosidodecahedron ${\displaystyle J_{78}}$, bigyrate diminished rhombicosidodecahedron ${\displaystyle J_{79}}$, parabidiminished rhombicosidodecahedron ${\displaystyle J_{80}}$, metabidiminished rhombicosidodecahedron ${\displaystyle J_{81}}$, gyrate bidiminished rhombicosidodecahedron ${\displaystyle J_{82}}$, and tridiminished rhombicosidodecahedron ${\displaystyle J_{83}}$.

References

1. ^ Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
2. Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. p. 62. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
3. ^ Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
4. Braileanu1, Patricia I.; Cananaul, Sorin; Pasci, Nicoleta E. (2022). "Geometric pattern infill influence on pentagonal cupola mechanical behavior subject to static external loads". Journal of Research and Innovation for Sustainable Society. 4 (2). Thoth Publishing House: 5–15. doi:10.33727/JRISS.2022.2.1:5-15 (inactive 16 December 2024). ISSN 2668-0416.{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) CS1 maint: numeric names: authors list (link)
5. Demey, Lorenz; Smessaert, Hans (2017). "Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation". Symmetry. 9 (10): 204. Bibcode:2017Symm....9..204D. doi:10.3390/sym9100204.
6. Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.

External links

• Weisstein, Eric W., "Pentagonal cupola" ("Johnson solid") at MathWorld.

• Elementary polyhedron
• Prismatoid polyhedra
• Johnson solids