
The Gall–Peters projection is a rectangular, equal-area map projection. Like all equal-area projections, it distorts most shapes. It is a cylindrical equal-area projection with latitudes 45° north and south as the regions on the map that have no distortion. The projection is named after James Gall and Arno Peters.
Gall described the projection in 1855 at a science convention and published a paper on it in 1885. Peters brought the projection to a wider audience beginning in the early 1970s through his "Peters World Map". The name "Gall–Peters projection" was first used by Arthur H. Robinson in a pamphlet put out by the American Cartographic Association in 1986.
The Gall–Peters projection achieved notoriety in the late 20th century as the centerpiece of a controversy about the political implications of map design.
Description

Formula
The projection is conventionally defined as:
where λ is the longitude from the central meridian in degrees, φ is the latitude, and R is the radius of the globe used as the model of the earth for projection. For longitude given in radians, remove the π/180° factors.
Simplified formula
Stripping out unit conversion and uniform scaling, the formulae may be written:
where is the longitude from the central meridian (in radians), is the latitude, and R is the radius of the globe used as the model of the earth for projection. Hence the sphere is mapped onto the vertical cylinder, and the cylinder is stretched to double its length. The stretch factor, 2 in this case, is what distinguishes the variations of cylindric equal-area projection.
Relation to cylindric equal-area projections
The various specializations of the cylindric equal-area projection differ only in the ratio of the vertical to horizontal axis. This ratio determines the standard parallel of the projection, which is the parallel at which there is no distortion and along which distances match the stated scale. The standard parallels of the Gall–Peters are 45° N and 45° S. Several other specializations of the equal-area cylindric have been described, promoted, or otherwise named.
Origins and naming
The Gall–Peters projection was first described in 1855 by the Scottish clergyman James Gall, who presented it along with two other projections at the Glasgow meeting of the British Association for the Advancement of Science (the BA). He gave it the name "orthographic" and formally published his work in 1885 in the Scottish Geographical Magazine. The projection is suggestive of the orthographic projection in that distances between parallels of the Gall–Peters are a constant multiple of the distances between the parallels of the orthographic. That constant is √2.
In 1967, the German filmmaker Arno Peters independently devised a similar projection, which he presented in 1973 as the "Peters world map". Peters's original description of his projection contained a geometric error that, taken literally, implies standard parallels of 46°02′ N/S. However the text accompanying the description made it clear that he had intended the standard parallels to be 45° N/S, making his projection identical to Gall's orthographic. In any case, the difference is negligible in a world map.
The name "Gall–Peters projection" seems to have been used first by Arthur H. Robinson in a pamphlet put out by the American Cartographic Association in 1986. Before 1973 it had been known, when referred to at all, as the "Gall orthographic" or "Gall's orthographic". Most Peters supporters refer to it as the "Peters projection". During the years of controversy, the cartographic articles tended to use one name or the other, while acknowledging both names. In recent years "Gall–Peters" seems to dominate.
Peters world map controversy

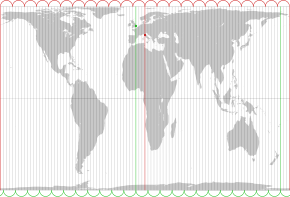
The Gall–Peters projection initially passed unnoticed when presented by Gall in 1855. It achieved more widespread attention after Arno Peters reintroduced it in 1973. He promoted it as a superior alternative to the commonly used Mercator projection, on the basis that the Mercator projection greatly distorts the relative sizes of regions on a map. In particular, he criticized that the Mercator projection causes wealthy Europe and North America to appear very large relative to poorer Africa and South America. These arguments swayed many socially concerned groups to adopt the Gall–Peters projection, including the National Council of Churches and the magazine New Internationalist.
His campaign was bolstered by the inaccurate claim that the Gall–Peters projection was the only "area-correct" map. In actuality, some of the oldest projections are equal-area (such as the sinusoidal projection), and hundreds have been described. He also inaccurately claimed that it possessed "absolute angle conformality", had "no extreme distortions of form", and was "totally distance-factual". Peters framed his criticisms of the Mercator projection with criticisms of the broader cartographic community. In particular, Peters wrote in The New Cartography,
By the authority of their profession have hindered its development. Since Mercator produced his global map over four hundred years ago for the age of Europeans world domination, cartographers have clung to it despite its having been long outdated by events. They have sought to render it topical by cosmetic corrections.… The cartographic profession is, by its retention of old precepts based on the Eurocentric global concept, incapable of developing this egalitarian world map which alone can demonstrate the parity of all peoples of the earth.
As Peters's promotions gained popularity, the cartographic community reacted with hostility to his criticisms, as well as to the inaccuracy and lack of novelty of his claims. They called attention to the long list of cartographers who, over the preceding century, had formally expressed frustration with publishers' overuse of the Mercator and advocated for alternatives. In addition, several scholars criticized the particularly large distortions present in the Gall–Peters projection, and remarked on the irony of its undistorted presentation of the mid latitudes, including Peters's native Germany, at the expense of the low latitudes, which host more of the technologically underdeveloped nations.
The increasing publicity of Peters's claims in 1986 motivated the American Cartographic Association (now Cartography and Geographic Information Society) to produce a series of booklets (including Which Map Is Best) designed to educate the public about map projections and distortion in maps. In 1989 and 1990, after some internal debate, seven North American geographic organizations adopted a resolution rejecting all rectangular world maps, a category that includes both the Mercator and the Gall–Peters projections, though the North American Cartographic Information Society notably declined to endorse it.
The two camps never made any real attempts toward reconciliation. The Peters camp largely ignored the protests of the cartographers, and did not acknowledge Gall's prior work until the controversy had largely run its course, late in Peters's life. While he likely devised the projection independently, his unscholarly conduct and refusal to engage the cartographic community undoubtedly contributed to the polarization and impasse.
In the ensuing decades, J. Brian Harley credited the Peters phenomenon with demonstrating the social implications of map projections.
Adoption
Maps based on the projection are promoted by UNESCO, and they are also widely used by British schools. The U.S. state of Massachusetts and Boston Public Schools began phasing in these maps in March 2017, becoming the first public school district and state in the United States to adopt Gall–Peters maps as their standard. Until its dissolution in 2020, Amherst-based ODT Maps Inc. was the exclusive North American publisher of Peters and Hobo–Dyer projection maps. On April 16, 2024, Nebraska Governor Jim Pillen signed a law that requires public schools to display maps based on the Gall–Peters projection, a similar cylindrical equal-area projection, or the AuthaGraph projection beginning in the 2024–2025 school year.
See also
- List of map projections
- Gall stereographic projection: another of Gall's projections.
References
Notes
- ^ Gall, James (1885). "Use of cylindrical projections for geographical, astronomical, and scientific purposes" (PDF). Scottish Geographical Magazine. 1 (4): 119–123. doi:10.1080/14702548508553829.
- ^ American Cartographic Association's Committee on Map Projections, 1986. Which Map is Best p. 12. Falls Church: American Congress on Surveying and Mapping.
- ^ Crampton, Jeremy (1994). "Cartography's defining moment: The Peters projection controversy, 1974–1990". Cartographica. 31 (4): 16–32. doi:10.3138/1821-6811-l372-345p.
- Snyder, John P. (1989). An Album of Map Projections p. 19. Washington, D.C.: U.S. Geological Survey Professional Paper 1453. (Mathematical properties of the Gall–Peters and related projections.)
- ^ Monmonier, Mark (2004). Rhumb Lines and Map Wars: A Social History of the Mercator Projection p. 152. Chicago: The University of Chicago Press. (Thorough treatment of the social history of the Mercator projection and Gall–Peters projections.)
- Smyth, C. Piazzi. (1870). On an Equal-Surface Projection and its Anthropological Applications. Edinburgh: Edmonton & Douglas. (Monograph describing an equal-area cylindric projection and its virtues, specifically disparaging Mercator's projection.)
- Maling, D.H. (1993). Coordinate Systems and Map Projections, second edition, second printing, p. 431. Oxford: Pergamon Press. ISBN 0-08-037234-1.
- "Ncc Friendship Press' Peters Projection Map".
- "The New Flat Earth". May 1983.
- ^ (1977) The Bulletin 25 (17) pp. 126–127. Bonn: Federal Republic of Germany Press and Information Office.
- ^ Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections p. 165. Chicago and London: The University of Chicago Press. ISBN 0-226-76746-9. (Summary of the Peters controversy.)
- Peters, Arno (1983). Die Neue Kartographie/The New Cartography (in German and English). Klagenfurt, Austria: Carinthia University; New York: Friendship Press.
- Snyder, John P. (1993). Flattening the Earth: Two Thousand Years of Map Projections p. 157. Chicago and London: The University of Chicago Press. ISBN 0-226-76746-9.
- Edwards, Trystan (1953). A New Map of the World. London: B.T. Batsford LTD.
- Hinks, Arthur R. (1912). Map Projections p. 29. London: Cambridge University Press.
- Steers, J.A. (1927). An Introduction to the Study of Map Projections 9th ed. p. 154. London: The University of London Press.
- Kellaway, G.P. (1946). Map Projections p. 37–38. London: Methuen & Co. LTD.
- Snyder, J.P. (1988). "Social Consciousness and World Maps". Christian Century. 105: 190–192.
- Robinson, Arthur H. (1985). "Arno Peters and His New Cartography". American Cartographer. 12 (2): 103–111. doi:10.1559/152304085783915063.
- Robinson, Arthur (1990). "Rectangular World Maps—No!". Professional Geographer. 42 (1): 101–104. doi:10.1111/j.0033-0124.1990.00101.x.
- American Cartographer. 1989. 16(3): 222–223.
- Wood, Denis (2003). "Cartography is Dead (Thank God!)". Cartographic Perspectives (45): 4–7. doi:10.14714/CP45.497.
Nearly the entire profession endorsed this idiotic resolution…(but not NACIS)
- Harley, J.B. (1991). "Can There Be a Cartographic Ethics?". Cartographic Perspectives. 10 (10): 9–16. doi:10.14714/CP10.1053.
- Higgins, Hannah B. The Grid Book. Cambridge, Massachusetts: MIT Press, 2009. ISBN 9780262512404 p.94. "Embroiled in controversy from the start, the map is nonetheless widely used in the British school system and is promoted by the United Nations Educational and Scientific Cultural Organization (UNESCO) because of its ability to communicate visually the actual relative sizes of the various regions of the planet."
- Joanna Walters (March 19, 2017). "Boston public schools map switch aims to amend 500 years of distortion". The Guardian. Retrieved March 19, 2017.
- Gardner, Sophia (August 2, 2021). "ODT's proportionate world maps find a fan in 'Don the donor'". Daily Hampshire Gazette. Northampton, Massachusetts. Archived from the original on August 3, 2021.
- "About Us". Amherst, Massachusetts: ODT Maps. 2021. Archived from the original on February 22, 2021.
- Wendling, Zach (April 11, 2024). "More than 100 bills sent to Nebraska Gov. Pillen for approval in legislative voting spree". Nebraska Examiner. States Newsroom.
- Legislative Bill 1329, Section 90 (PDF). Nebraska Legislature. 2024. pp. 102–103.
- "LB1329". Nebraska Legislature. Lincoln, Nebraska: Nebraska Legislature. April 18, 2024. Retrieved May 15, 2024.
Further reading
- Snyder, John P. (1987), Map Projections—A Working Manual: U.S. Geological Survey Professional Paper 1395, Washington: Government Printing Office. https://pubs.er.usgs.gov/publication/pp1395.
External links
- The Size of the Matter—An article in The Times of India on why the Gall–Peters projection should be more widely used.
- Peters Projection vs. Mercator Projection Archived 2016-04-10 at the Wayback Machine—A critique of the importance of the Gall–Peters projection.


 is the longitude from the central meridian (in radians),
is the longitude from the central meridian (in radians),  is the latitude, and R is the radius of the globe used as the model of the earth for projection. Hence the sphere is mapped onto the vertical cylinder, and the cylinder is stretched to double its length. The stretch factor, 2 in this case, is what distinguishes the variations of cylindric equal-area projection.
is the latitude, and R is the radius of the globe used as the model of the earth for projection. Hence the sphere is mapped onto the vertical cylinder, and the cylinder is stretched to double its length. The stretch factor, 2 in this case, is what distinguishes the variations of cylindric equal-area projection.