
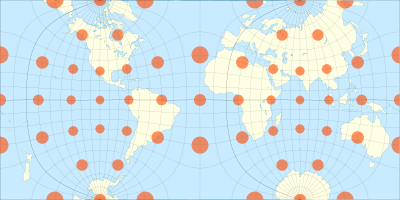
The Guyou hemisphere-in-a-square projection is a conformal map projection for the hemisphere. It is an oblique aspect of the Peirce quincuncial projection.
History
The projection was developed by Émile Guyou [fr] of France in 1887.
Formal description
The projection can be computed as an oblique aspect of the Peirce quincuncial projection by rotating the axis 45 degrees. It can also be computed by rotating the coordinates −45 degrees before computing the stereographic projection; this projection is then remapped into a square whose coordinates are then rotated 45 degrees.
The projection is conformal except for the four corners of each hemisphere's square. Like other conformal polygonal projections, the Guyou is a Schwarz–Christoffel mapping.
Properties
Its properties are very similar to those of the Peirce quincuncial projection:
- Each hemisphere is represented as a square, the sphere as a rectangle of aspect ratio 2:1.
- The part where the exaggeration of scale amounts to double that at the centre of each square is only 9% of the area of the sphere, against 13% for the Mercator and 50% for the stereographic
- The curvature of lines representing great circles is, in every case, very slight, over the greater part of their length.
- It is conformal everywhere except at the corners of the square that corresponds to each hemisphere, where two meridians change direction abruptly twice each; the Equator is represented by a horizontal line.
- It can be tessellated in all directions.
Related projections
- The Adams hemisphere-in-a-square projection and the Peirce quincuncial projection are different aspects of the same underlying Schwarz–Christoffel mapping. Such mappings are transformations of half a stereographic projection.
See also
References
- E. Guyou (1887) "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator", Annales Hydrographiques, Ser. 2, Vol. 9, 16–35. https://www.retronews.fr/journal/annales-hydrographiques/1-janvier-1887/1877/4868382/23
- Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- Lee, L. P. (1976). Conformal Projections Based on Elliptic Functions. Cartographica Monographs. Vol. 16. Toronto: B. V. Gutsell, York University. ISBN 0-919870-16-3. Supplement No. 1 to The Canadian Cartographer 13.
- ^ C.S. Peirce (December 1879). "A Quincuncial Projection of the Sphere". American Journal of Mathematics. 2 (4). The Johns Hopkins University Press: 394–396. doi:10.2307/2369491. JSTOR 2369491.