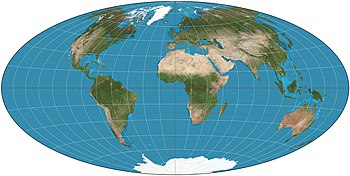
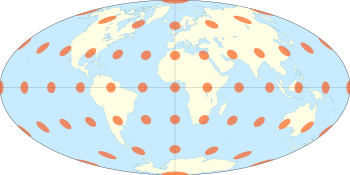
The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide.
Development
Directly inspired by the Aitoff projection, Hammer suggested the use of the equatorial form of the Lambert azimuthal equal-area projection instead of Aitoff's use of the azimuthal equidistant projection:
where laeax and laeay are the x and y components of the equatorial Lambert azimuthal equal-area projection. Written out explicitly:
The inverse is calculated with the intermediate variable
The longitude and latitudes can then be calculated by
where λ is the longitude from the central meridian and φ is the latitude.
Visually, the Aitoff and Hammer projections are very similar. The Hammer has seen more use because of its equal-area property. The Mollweide projection is another equal-area projection of similar aspect, though with straight parallels of latitude, unlike the Hammer's curved parallels.
Briesemeister
William A. Briesemeister presented a variant of the Hammer in 1953. In this version, the central meridian is set to 10°E, the coordinate system is rotated to bring the 45°N parallel to the center, and the resulting map is squashed horizontally and reciprocally stretched vertically to achieve a 7:4 aspect ratio instead of the 2:1 of the Hammer. The purpose is to present the land masses more centrally and with lower distortion.
Nordic
Before projecting to Hammer, John Bartholomew rotated the coordinate system to bring the 45° north parallel to the center, leaving the prime meridian as the central meridian. He called this variant the "Nordic" projection.
See also
References
- Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 130–133, ISBN 0-226-76747-7.
- Weisstein, Eric W. "Hammer–Aitoff Equal-Area Projection." From MathWorld—A Wolfram Web Resource
- Briesemeister, William (April 1953). "A new oblique equal-area projection". Geographical Review. 43 (2): 260–261. doi:10.2307/211940. Retrieved 2024-01-18.
- ^ Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 162. ISBN 978-0160033681. Archived from the original on 2010-07-01. Retrieved 2018-03-29.



